THEOREM 7.8
Soient E un K-espace vectoriel de dimension finie et F un sous-espace
vectoriel de E, on suppose que E est de dimension finie, alors :
- F est un K-espace vectoriel de dimension finie
-
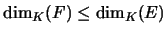
- si
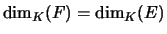 , alors
, alors 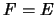 .
.
- Démonstration : soit L une partie libre de F, c'est donc a
fortiori une partie libre de E. D'après, par exemple, le
théorème de la base incomplète, le cardinal de L est
inférieur ou égal à
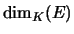 . Il suffit donc de prendre
dans F une partie libre ayant le nombre maximum d'éléments pour
avoir une partie basique de F. Ainsi F admet une base finie ayant un
cardinal inférieur ou égal à
. Il suffit donc de prendre
dans F une partie libre ayant le nombre maximum d'éléments pour
avoir une partie basique de F. Ainsi F admet une base finie ayant un
cardinal inférieur ou égal à 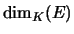 . Si
. Si
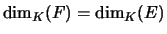 , alors une base quelconque de F est une partie libre
de E ayant le bon nombre d'éléments (théorème ??), c'est
donc aussi une base de E, i.e.
, alors une base quelconque de F est une partie libre
de E ayant le bon nombre d'éléments (théorème ??), c'est
donc aussi une base de E, i.e. 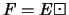
La partie 3. du théorème précédent est fondamentale dans
les exercices. Elle permet en effet de démontrer que deux K-espaces
vectoriels de dimension finie sont égaux si et seulement si l'un des
deux est inclus dans l'autre et s'ils ont la même dimension (alors
qu'autrement il faudrait montrer deux inclusions).
- Exemples :
- Soit D une droite vectorielle, les seuls sous-espaces vectoriels de D
sont {0} et D.
- Soit P un plan vectoriel, les seuls sous-espaces vectoriels de P sont
{0}, les droites vectorielles contenues dans P et P lui-même.
Le but de ce paragraphe est d'établir une formule attribuée à
Grassmann donnant la dimension de la somme de deux sous-espaces vectoriels
d'un K-espace vectoriel E de dimension finie, et d'en déduire ses
principales conséquences.
PROPOSITION 7.4
Soient
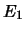
et
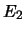
deux K-espaces vectoriels de dimension finie,
alors
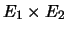
est de dimension finie et on a
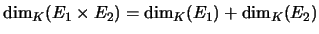
.
- Démonstration : en effet, on pose
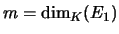 ,
,
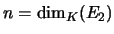 et on choisit
et on choisit
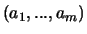 une base de
une base de 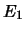 ,
,
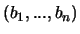 une base de
une base de 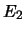 . On laisse au lecteur consciencieux
le soin de vérifier que le
. On laisse au lecteur consciencieux
le soin de vérifier que le 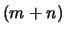 -uplet
-uplet
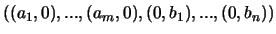 est une base de
est une base de
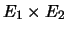 . On peut aussi vérifier que
. On peut aussi vérifier que
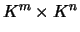 est
isomorphe à
est
isomorphe à
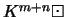
THEOREM 7.9 (dimension d'une somme directe)
Soient E un K-espace vectoriel de dimension finie, 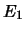 et
et 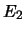 deux
sous-espaces vectoriels de E dont la somme est directe, on a alors la
relation :
deux
sous-espaces vectoriels de E dont la somme est directe, on a alors la
relation :
De plus, si
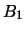
est une partie basique de
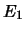
et
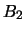
une partie
basique de
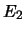
,
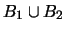
est une partie basique de
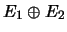
.
- Démonstration : il suffit bien entendu de montrer la seconde
asertion. On peut remarquer que
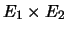 et
et
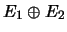 sont isomorphes et appliquer la proposition précédente
sont isomorphes et appliquer la proposition précédente
- Exercices :
- Rédiger les démonstrations de la proposition ?? et du
théorème ??. Montrer aussi que dans ce dernier l'hypothèse ''E
est de dimension finie'' peut être remplacée par ''
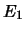 et
et 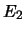 sont deux sous-espaces vectoriels de dimension finie''.
sont deux sous-espaces vectoriels de dimension finie''.
- Généraliser la proposition ?? et le théorème ?? au
cas d'un nombre fini quelconque d'espaces vectoriels. On obtiendra ainsi
les formules :
THEOREM 7.10 (existence d'un supplémentaire)
Soient E un K-espace vectoriel de dimension finie et F un sous-espace
vectoriel de E, alors F admet au moins un supplémentaire dans E. De
plus, tous les supplémentaires de F dans E ont la même dimension
(appelée parfois codimension de F dans ).
- Démonstration : soit B une partie basique de F (qui est de
dimension finie), d'après le théorème de la base incomplète,
on peut trouver une partie C de E disjointe de B telle que
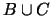 soit
une partie basique de E. Il est alors quasi évident que le sous-espace
vectoriel G engendré par C est un supplémentaire de F. En effet, on
pose
soit
une partie basique de E. Il est alors quasi évident que le sous-espace
vectoriel G engendré par C est un supplémentaire de F. En effet, on
pose
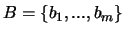 et
et
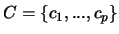 . Soit x quelconque
de E, il se décompose de façon unique sur la partie basique
. Soit x quelconque
de E, il se décompose de façon unique sur la partie basique 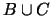 , i.e.
, i.e.
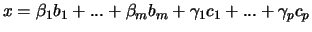 . Or
. Or
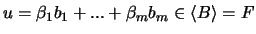 et
et
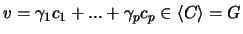 , donc
, donc 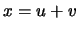 avec
avec 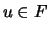 et
et 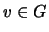 , ce
qui démontre que
, ce
qui démontre que 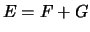 . Par ailleurs, l'unicité de la
décomposition de x sur
. Par ailleurs, l'unicité de la
décomposition de x sur 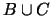 entraîne l'unicité de
l'écriture
entraîne l'unicité de
l'écriture 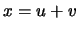 , avec
, avec 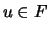 ,
, 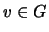 , la somme est donc directe.
Enfin, soit G un supplémentaire quelconque de F dans E, on a
, la somme est donc directe.
Enfin, soit G un supplémentaire quelconque de F dans E, on a 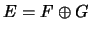 , et d'après le théorème ??,
, et d'après le théorème ??,
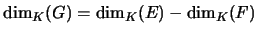 , la dimension de G est donc indépendante du supplémentaire
choisi
, la dimension de G est donc indépendante du supplémentaire
choisi
On remarque que l'on a donné, sans démonstration, un résultat
plus général : tout sous-espace vectoriel admet au moins un
supplémentaire (sans condition de dimension). La démonstration du
théorème éclaire un peu le phénomène. Le lecteur pourra
prouver que dans un espace vectoriel de dimension 3, un plan vectoriel P
admet pour supplémentaire toute droite vectorielle non contenue dans P.
THEOREM 7.11 (formule de Grassmann)
Soient E un K-espace vectoriel de dimension finie, 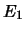 et
et 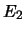 deux
sous-espaces vectoriels de E, on a la relation :
deux
sous-espaces vectoriels de E, on a la relation :
- Démonstration : il existe de nombreuses preuves de ce
résultat. On esquisse ici une démonstration directe (ce n'est pas la
plus jolie) et on renvoie le lecteur à la section suivante pour une
preuve élégante). L'astuce consiste à se ramener à une somme
directe. L'inclusion
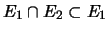 permet de choisir un
supplémentaire F de
permet de choisir un
supplémentaire F de
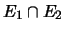 dans
dans 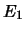 . Ainsi
. Ainsi
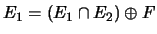 . On en déduit que
. On en déduit que
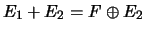 . En effet,
. En effet,
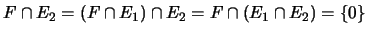 et il est clair que
et il est clair que
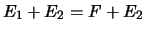 (
(
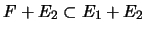 est évidente, l'autre inclusion se vérifie facilement).
Ainsi, en appliquant le théorème ??, on trouve :
est évidente, l'autre inclusion se vérifie facilement).
Ainsi, en appliquant le théorème ??, on trouve :
d'où le résultat en éliminant
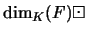
THEOREM 7.12
Soient
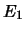
et
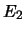
deux sous-espaces vectoriels d'un K-espace
vectoriel E de dimension finie E, on considère les trois
propriétés suivantes :
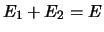
-
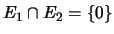
-
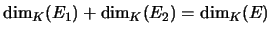 .
.
Alors deux quelconques de ces propriétés entraînent la
troisième, et
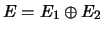 . Réciproquement, si
. Réciproquement, si
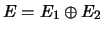 les trois propriétés sont vérifiées.
les trois propriétés sont vérifiées.
- Démonstration : si 1. et 2. sont réalisées, alors on sait
que
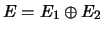 et la propriété 3. n'est autre que le
théorème ??
et la propriété 3. n'est autre que le
théorème ??
- Si 1. et 3. sont réalisées, la formule de Grassmann
entraîne que
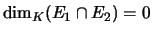 , donc
, donc
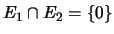 .
.
- Si 2. et 3. sont réalisées, la formule de Grassmann devient
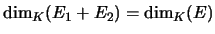 . Or
. Or
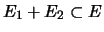 , le
théorème ?? montre alors que
, le
théorème ?? montre alors que 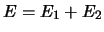 . Enfin, la
réciproque est triviale
. Enfin, la
réciproque est triviale
- Exercices :
- Montrer que, dans la formule de Grassmann, l'hypothèse ''E est de
dimension finie'' peut être remplacée par l'hypothèse plus
faible ''
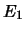 et
et 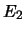 sont deux sous-espaces vectoriels de dimension
finie''.
sont deux sous-espaces vectoriels de dimension
finie''.
- Dans R
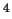 on considère le sous-espace vectoriel
on considère le sous-espace vectoriel 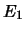 engendré par
engendré par 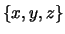 avec
avec 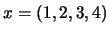 ,
, 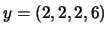 ,
, 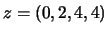 , et le sous-espace vectoriel
, et le sous-espace vectoriel 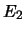 engendré par
engendré par 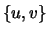 avec
avec 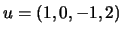 et
et 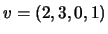 . Vérifier sur cet exemple la
formule de Grassmann.
. Vérifier sur cet exemple la
formule de Grassmann.
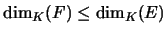
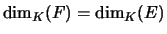 , alors
, alors 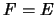 .
.
![]() et
et ![]() deux
sous-espaces vectoriels de E dont la somme est directe, on a alors la
relation :
deux
sous-espaces vectoriels de E dont la somme est directe, on a alors la
relation :
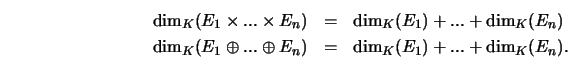
![]() et
et ![]() deux
sous-espaces vectoriels de E, on a la relation :
deux
sous-espaces vectoriels de E, on a la relation :
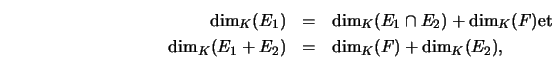
![]() . Réciproquement, si
. Réciproquement, si
![]() les trois propriétés sont vérifiées.
les trois propriétés sont vérifiées.