A conceptually simple approach to a representation of the weight sequence
![]() is to describe the shape of the weight
function
is to describe the shape of the weight
function ![]() by a density function
with a scale parameter that adjusts the size and the form
of the weights near
by a density function
with a scale parameter that adjusts the size and the form
of the weights near ![]() . It is quite common to refer to
this shape function as a kernel K.
The kernel is a continuous, bounded and symmetric
real function
. It is quite common to refer to
this shape function as a kernel K.
The kernel is a continuous, bounded and symmetric
real function ![]() which integrates to one,
which integrates to one,
The weight sequence for kernel smoothers (for one-dimensional ![]() ) is defined by
) is defined by
and where

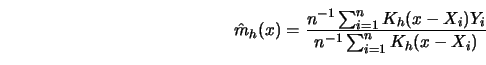
A plot of this so-called Epanechnikov kernel is given in Figure 3.1.
![\includegraphics[scale=0.7]{ANRepa.ps}](anrhtmlimg214.gif)
|
Note that this kernel is not differentiable at ![]() .
The kernel smoother is not defined for a
bandwidth with
.
The kernel smoother is not defined for a
bandwidth with
![]() .
If such a ``0/0" case occurs one defines
.
If such a ``0/0" case occurs one defines ![]() as being 0.
Suppose that the kernel estimator is only evaluated at the observations
as being 0.
Suppose that the kernel estimator is only evaluated at the observations
![]() . Then, as
. Then, as ![]()
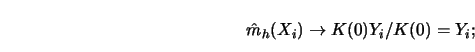
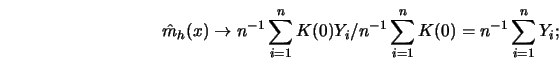
How does this Epanechnikov kernel act on real data and what is the shape
of the weights
![]() ? To obtain some insight,
consider the food versus net income data again (see Figures
2.1 and 2.2).
The economist is interested in estimating
the so-called statistical Engel curve, the
average expenditure for food given a certain level of income. Kernel
smoothing is a possible procedure for estimating this
curve. The kernel
weights
? To obtain some insight,
consider the food versus net income data again (see Figures
2.1 and 2.2).
The economist is interested in estimating
the so-called statistical Engel curve, the
average expenditure for food given a certain level of income. Kernel
smoothing is a possible procedure for estimating this
curve. The kernel
weights
![]() depend on the values of the
depend on the values of the ![]() -observations
through the density estimate
-observations
through the density estimate ![]() .
In Figure 3.2 the effective weight function for estimating this Engel
curve for food in 1973 is shown centered
at
.
In Figure 3.2 the effective weight function for estimating this Engel
curve for food in 1973 is shown centered
at ![]() for the bandwidths
for the bandwidths ![]() 0.1, 0.2, 0.3. Note
that the effective weight function depends only on the
0.1, 0.2, 0.3. Note
that the effective weight function depends only on the ![]() -values.
-values.
![\includegraphics[scale=0.7]{ANRpotakernel.ps}](anrhtmlimg232.gif)
|
One can learn two things from this picture. First, it is obvious that
the smaller the bandwidth, the more concentrated are the weights around
![]() . Second, in regions of sparse data where the marginal density
estimate
. Second, in regions of sparse data where the marginal density
estimate ![]() is small, the sequence
is small, the sequence
![]() gives
more weight to observations around
gives
more weight to observations around ![]() . Indeed, around
. Indeed, around ![]() the
density estimate
the
density estimate ![]() reaches its maximum
and at
reaches its maximum
and at ![]() the density is roughly a tenth of
the density is roughly a tenth of ![]() .
(See Figure 1.5 for the year=1973 which is the fourth density contour
counting from the front.)
.
(See Figure 1.5 for the year=1973 which is the fourth density contour
counting from the front.)
For multidimensional predictor variables
![]() one
can use a multidimensional product kernel function
one
can use a multidimensional product kernel function
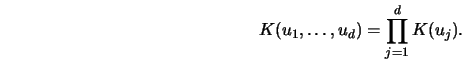
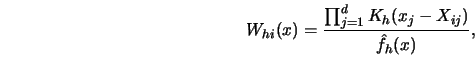
There are cases of applications
for which the density ![]() of the
of the ![]() -variables is known.
The kernel weights that have been investigated for this sampling scheme
are (Greblicki (1974); Johnston (1979) Johnston (1982);
Greblicki and Krzyzak (1980) and Georgiev (1984a),Georgiev (1984b))
-variables is known.
The kernel weights that have been investigated for this sampling scheme
are (Greblicki (1974); Johnston (1979) Johnston (1982);
Greblicki and Krzyzak (1980) and Georgiev (1984a),Georgiev (1984b))
Often the ![]() -observations are taken at regular distances and form
an equidistant grid of points of some interval. Examples are
observations from longitudinal data or discretized analog processes;
see Müller (1987). Without loss of
generality we can assume that the
-observations are taken at regular distances and form
an equidistant grid of points of some interval. Examples are
observations from longitudinal data or discretized analog processes;
see Müller (1987). Without loss of
generality we can assume that the ![]() -observations have been taken
in the unit interval
-observations have been taken
in the unit interval ![]() .
In this case, one could use the
modified kernel weights
.
In this case, one could use the
modified kernel weights
![]() with
with ![]() ,
the density of the uniform distribution on
,
the density of the uniform distribution on ![]() .
In the fixed design model of nearly equispaced, nonrandom
.
In the fixed design model of nearly equispaced, nonrandom
![]() on
on ![]() ,
Priestley and Chao (1972) and Benedetti (1977) considered the
weight sequence
,
Priestley and Chao (1972) and Benedetti (1977) considered the
weight sequence
The weights
![]() are related to
the so-called convolution smoothing as defined by
Clark (1980); see
Exercise 3.1.3
The weight sequences
are related to
the so-called convolution smoothing as defined by
Clark (1980); see
Exercise 3.1.3
The weight sequences
![]() and
and
![]() have been mostly used in the fixed design model.
Theoretical analysis of this stochastic behavior in the random design model
indicates that they have different variance compared to
the Nadaraya-Watson kernel smoother; see Section 3.11.
have been mostly used in the fixed design model.
Theoretical analysis of this stochastic behavior in the random design model
indicates that they have different variance compared to
the Nadaraya-Watson kernel smoother; see Section 3.11.
The consistency of the kernel smoother
![]() with the Nadaraya-Watson weights
with the Nadaraya-Watson weights ![]() defined by
3.1.2 is shown in the following proposition. The proof of consistency
of the
other weight sequences is very similar and is deferred to exercises.
defined by
3.1.2 is shown in the following proposition. The proof of consistency
of the
other weight sequences is very similar and is deferred to exercises.
30pt
to 30pt(A1)
![]()
30pt
to 30pt(A2)
![]()
30pt
to 30pt(A3)
![]()
30pt
to 30pt(A4)
![]() .
.
Then, at every point of continuity of ![]() ,
, ![]() and
and
![]() , with
, with ![]()
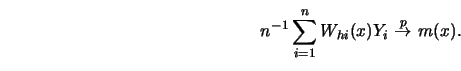
The proof of this proposition is in the Complements of this section.
The above result states that the kernel smoother converges in probability to
the true response curve ![]() .
It is natural to ask how fast this
convergence is going to happen. The mean squared error
.
It is natural to ask how fast this
convergence is going to happen. The mean squared error
![\begin{displaymath}d_M(x, h) = E [\hat m_h (x) - m(x)]^2\end{displaymath}](anrhtmlimg261.gif)


30pt
to 30pt(A0) ![]() has support
has support ![]() with
with ![]()
30pt
to 30pt(A1)
![]()
30pt
to 30pt(A2)
![]()
30pt
to 30pt(A3)
![]()
30pt
to 30pt(A4)
![]()
Then
![\begin{displaymath}d_M(x, h) \approx (nh)^{-1} \sigma^2 c_K + h^4 d_K^2 [m''(x)]^2 /4. \end{displaymath}](anrhtmlimg270.gif)
The mean squared error splits up into the two parts, variance and bias![]() .
The above theorem says that the bias, as a function of
.
The above theorem says that the bias, as a function of ![]() , is increasing
whereas the variance is decreasing. By this qualitative behavior one gets a
feeling of what the smoothing problem is about:
, is increasing
whereas the variance is decreasing. By this qualitative behavior one gets a
feeling of what the smoothing problem is about:
The kernel weights define a neighborhood of points around a grid
point ![]() . Let us investigate the question of fitting a polynomial in such a
neighborhood.
. Let us investigate the question of fitting a polynomial in such a
neighborhood.
The simplest polynomial to fit in such a neighborhood is a
constant.
There is a striking similarity between local polynomial fitting and
kernel smoothing.
For fixed ![]() , the kernel estimator
, the kernel estimator ![]() with positive weights
with positive weights ![]() is the
solution to the following minimization problem
is the
solution to the following minimization problem
This question is investigated in the fixed design model.
Consider equispaced
![]() , and a local parabolic fit. Let us take a point
, and a local parabolic fit. Let us take a point ![]() that is not too close to the boundary of the observation interval. (The
behavior of kernel smoothers at the boundary is discussed in Section
4.4.)
Consider a uniform kernel
that is not too close to the boundary of the observation interval. (The
behavior of kernel smoothers at the boundary is discussed in Section
4.4.)
Consider a uniform kernel
![]() which
parameterizes the neighborhood around
which
parameterizes the neighborhood around ![]() .
We have then to minimize
.
We have then to minimize
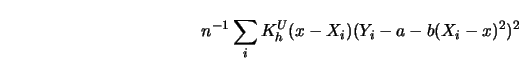
Define ![]() as
as
![]() and approximate
and approximate
![]() by one.
For large
by one.
For large ![]() , the sum
, the sum
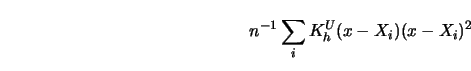

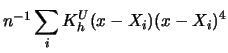 shows that the normal equations (3.1.9-3.1.10) can be rewritten as
shows that the normal equations (3.1.9-3.1.10) can be rewritten as
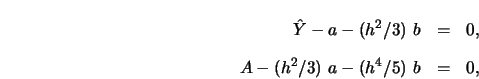
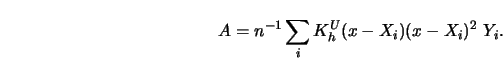
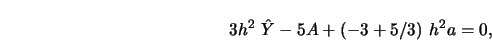
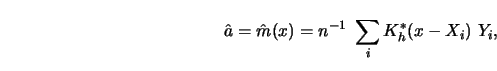
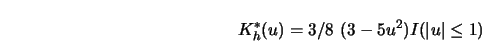
![\includegraphics[scale=0.15]{ANR3,3.ps}](anrhtmlimg300.gif)
|
The equivalence of local polynomial fitting and kernel smoothing
has been studied in great detail by Müller (1987). Some numerical
comparison has been done by Schmerling and Peil (1985, figure 1).
They used a Gaussian kernel weight sequence with kernel
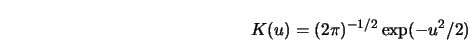
The technique of kernel estimation can also be used to estimate
derivatives of the regression function. Kernel derivative
estimators are defined by differentiating the weight function
sequence with respect to ![]() . If the weights are sufficiently smooth
and the bandwidth sequence is correctly tuned then these estimators
will converge to the corresponding derivatives of
. If the weights are sufficiently smooth
and the bandwidth sequence is correctly tuned then these estimators
will converge to the corresponding derivatives of ![]() .
This can be
easily illustrated in the equidistant design setting with the kernel
smoother, using the Priestley-Chao weights
.
This can be
easily illustrated in the equidistant design setting with the kernel
smoother, using the Priestley-Chao weights
![]() .
Taking the
.
Taking the ![]() -th derivative with respect to
-th derivative with respect to ![]() gives
gives
![\begin{displaymath}c^{(k)}_K = \int {[K^{(k)}]}^2(u) du,\end{displaymath}](anrhtmlimg303.gif)

30pt
to 30pt(A0)
![]() has support
has support ![]() with
with
![]() ,
,
30pt
to 30pt(A1)
![]()
30pt
to 30pt(A2)
![]() ,
,
30pt
to 30pt(A3)
![]() ,
,
30pt
to 30pt(A4)
![]() .
.
Then
![\begin{displaymath}d_M(x, h) \approx (nh^{2k+1})^{-1} \sigma^2 c^{(k)}_K
+ h^4 {d^{(k)}_K}^2 {[m^{(k+2)}(x)]}^2/(k+2)!^2. \end{displaymath}](anrhtmlimg311.gif)
A sketch of the proof of this proposition is given in the Complements to this
section.
Gasser and Müller (1984) studied slightly different weights based on
derivatives of
![]() .
In view of the asymptotic equivalence
of the weight functions
.
In view of the asymptotic equivalence
of the weight functions
![]() and
and
![]() (see Exercise 3.1.3) it is not surprising that the Gasser-Müller kernel
estimator has the same mean squared error expansion as given in Proposition
3.1.2 Figure 3.4 is taken from
an application of the Gasser-Müller method,
in which they compute the velocity
and acceleration of height growth.
The upper graphs compare the growth velocity (first derivative) of boys
to that of girls. The graphs below depicts the growth accelerations (second
derivatives) for the two sexes.
(see Exercise 3.1.3) it is not surprising that the Gasser-Müller kernel
estimator has the same mean squared error expansion as given in Proposition
3.1.2 Figure 3.4 is taken from
an application of the Gasser-Müller method,
in which they compute the velocity
and acceleration of height growth.
The upper graphs compare the growth velocity (first derivative) of boys
to that of girls. The graphs below depicts the growth accelerations (second
derivatives) for the two sexes.
![\includegraphics[scale=0.25]{ANR3,4.ps}](anrhtmlimg312.gif)
|
In the case of non-equally spaced and random ![]() -variables the
weight sequence becomes more complicated. The principle of
differentiating the kernel weights to obtain kernel estimates for
derivatives of the regression function also works here. For instance,
the first derivative
-variables the
weight sequence becomes more complicated. The principle of
differentiating the kernel weights to obtain kernel estimates for
derivatives of the regression function also works here. For instance,
the first derivative
![]() could be estimated using the
effective weight sequence
could be estimated using the
effective weight sequence

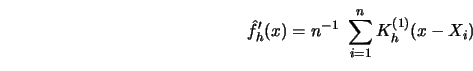
Suppose that it is desired to compute the Nadaraya-Watson kernel
estimate at ![]() distinct points. A direct application of formula
(3.1.2) for a
kernel with unbounded support would result in
distinct points. A direct application of formula
(3.1.2) for a
kernel with unbounded support would result in ![]() operations for
determination of the estimator at
operations for
determination of the estimator at ![]() gridpoints. Some computer time can be
saved by using kernels with bounded support, say
gridpoints. Some computer time can be
saved by using kernels with bounded support, say ![]() .
Local averaging is then performed
only in a neighborhood of size
.
Local averaging is then performed
only in a neighborhood of size ![]() around the gridpoints.
The number of
operations would then be
around the gridpoints.
The number of
operations would then be ![]() since about
since about ![]() points fall into an
interval of length
points fall into an
interval of length ![]() .
Since
.
Since ![]() tends to zero, the introduction
of kernels with bounded support looks like a drastic improvement.
tends to zero, the introduction
of kernels with bounded support looks like a drastic improvement.
For optimization of the smoothing
parameter one needs to repeat kernel smoothing several times and so even for
moderate sample size the algorithm would still be extremely slow.
More efficient kernel smoothing algorithms can be defined by first
discretizing the data into bins of the form
![\begin{displaymath}B(x;x_0,h) = [x_0+kh,x_0+(k+1)h]\end{displaymath}](anrhtmlimg322.gif)
The computational
advantage comes from building a weighted average of rounded points
(WARP). In particular, consider the set of ``origins"
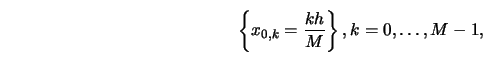
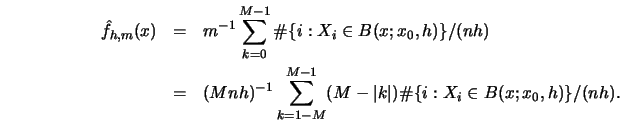
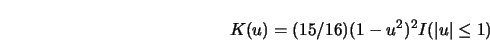
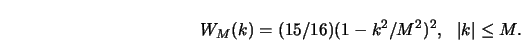
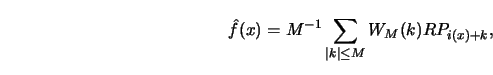
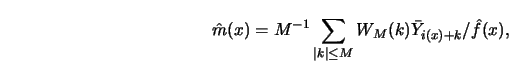
Another technique uses Fourier transforms
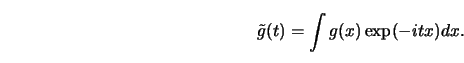
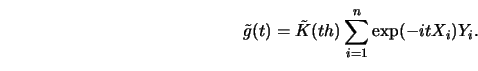


Exercises
3.1.1Recall the setting for the weight sequence
![]() .
Consider linear interpolation
between two successive observations
.
Consider linear interpolation
between two successive observations
![]() and
and ![]() with
with
![]() ,
,
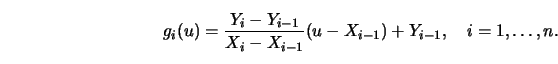
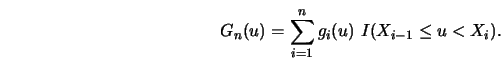
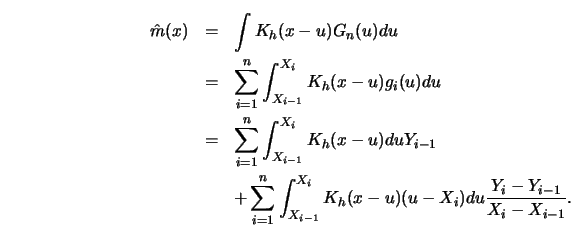
3.1.2Discuss the behavior of the kernel estimator when a single observation moves
to a very large value, that is, study the case
![]() with
with ![]() for a fixed
for a fixed ![]() . How does the curve change under such a
distortion?
What will happen for a distortion in
. How does the curve change under such a
distortion?
What will happen for a distortion in ![]() -direction
-direction
![]() ?
?
3.1.3When we had the situation of equispaced
![]() we said that a local
linear fit would not make much sense with a symmetric kernel weight.
Consider now the situation of random
we said that a local
linear fit would not make much sense with a symmetric kernel weight.
Consider now the situation of random ![]() s.
Would you expect a gain in
using a local linear fit now?
s.
Would you expect a gain in
using a local linear fit now?
3.1.4Prove in analogy to Proposition 3.1.1 the asymptotic mean squared error
decomposition of kernel smoothers with weight sequences
![]() and
and
![]() , respectively.
, respectively.
3.1.5Recall the the weighted local fitting of polynomials.
If the order of the approximating polynomial
![]() is
is ![]() then
then ![]() is just the ordinary kernel estimate with weights
is just the ordinary kernel estimate with weights
![]() For a local linear approximation
one has
For a local linear approximation
one has
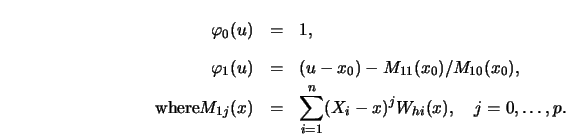
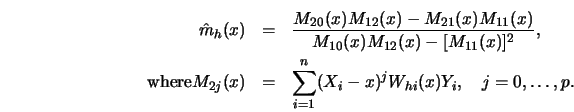
3.1.6Verify that the kernel ![]() from the local parabolic fit (see
3.1.13) is
indeed a kernel and has vanishing first, second and third moments.
from the local parabolic fit (see
3.1.13) is
indeed a kernel and has vanishing first, second and third moments.
3.1.7Consider the positive food versus net income data set.
Suppose you are asked
to do a kernel smooth at the right end.
What can happen
if the kernel ![]() has negative ``sidelobes", that is, the tails of
has negative ``sidelobes", that is, the tails of ![]() are
allowed to take on negative values?
are
allowed to take on negative values?
3.1.8Give a rigorous proof of Proposition 3.1.2 (A sketch of the proof is in the
Complements of this section.) Compare the remainder terms of the bias
approximations for the weight sequence
![]() with those
of the weight sequence
with those
of the weight sequence
![]()
3.1.9Derive that the rate of convergence of ![]() from Theorem
3.1.1 is
from Theorem
3.1.1 is ![]() and
is chosen optimally, that is,
and
is chosen optimally, that is,
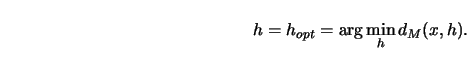
3.1.10Show the asymptotic equivalence of the weight sequences
![]() and
and
![]() in the following sense
in the following sense
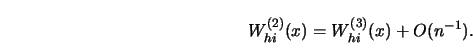
3.1.11Give reasons why
![]() , as in the weight
sequence (3.1.6), is a reasonable choice for a density estimate.
[Hint: Consider the asymptotic distribution of the spacings
, as in the weight
sequence (3.1.6), is a reasonable choice for a density estimate.
[Hint: Consider the asymptotic distribution of the spacings
![]() .]
.]