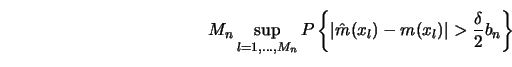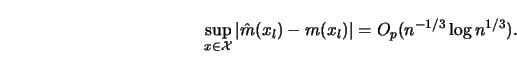In parametric problems the speed at which estimated parameters tend to the
true value is typically ![]() (Bickel and Doksum 1977, chapter 4.4). By
contrast, in the nonparametric curve estimation setting, the rate of
convergence, if quantified, for instance, by the square root of the quadratic
deviation, is usually of slower order
(Bickel and Doksum 1977, chapter 4.4). By
contrast, in the nonparametric curve estimation setting, the rate of
convergence, if quantified, for instance, by the square root of the quadratic
deviation, is usually of slower order
![]() . The subject of this
section is to shed some light on the dependence of this rate
. The subject of this
section is to shed some light on the dependence of this rate ![]() on four
important qualitative features of regression smoothing,
on four
important qualitative features of regression smoothing,
Other distance measures, for example, the uniform deviation
![]() , depend also on these four characteristics of regression smoothing but
might have a slightly different rate. Consider for the moment just the mean
integrated squared error
, depend also on these four characteristics of regression smoothing but
might have a slightly different rate. Consider for the moment just the mean
integrated squared error
![]() for which we would like to analyze
the speed of convergence.
Let
for which we would like to analyze
the speed of convergence.
Let ![]() be a sequence of positive constants. It
is called a lower rate of convergence if for some
be a sequence of positive constants. It
is called a lower rate of convergence if for some ![]() and
and ![]()


So far the concept of optimal rates of convergence has been defined through
the mean integrated squared error (MISE) ![]() . It turns out that for kernel
estimators one could equally well have stated the concept of optimal rates
with the integrated squared error
. It turns out that for kernel
estimators one could equally well have stated the concept of optimal rates
with the integrated squared error ![]() or some other distance measure, such as
or some other distance measure, such as
![]() ; see Härdle (1986b).
Asymptotically they define distance measures of
equal sharpness, as is shown in the following theorem by Marron and Härdle
(1986, theorem 3.4).
; see Härdle (1986b).
Asymptotically they define distance measures of
equal sharpness, as is shown in the following theorem by Marron and Härdle
(1986, theorem 3.4).
30pt
to 30pt(A1)
![]() ,
, ![]()
30pt
to 30pt(A2) ![]() is Hölder continuous and is positive on the support
of
is Hölder continuous and is positive on the support
of ![]() ;
;
30pt
to 30pt(A3) ![]() is Hölder continuous.
is Hölder continuous.
Then for kernel estimators
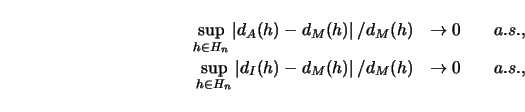
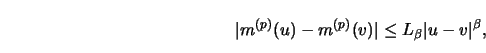
30pt
to 30pt(A1) ![]() is the indicator function of the compact set
is the indicator function of the compact set ![]() ;
;
30pt
to 30pt(A2) the conditional distribution of ![]() given
given ![]() is normal
with variance
is normal
with variance ![]() ;
;
30pt
to 30pt(A3) the conditional variance ![]() is bounded from above as
well as bounded from zero on some compact set
is bounded from above as
well as bounded from zero on some compact set
![]() ;
;
30pt
to 30pt(A4) the marginal density ![]() is bounded away from zero on
is bounded away from zero on
![]() ;
;
30pt
to 30pt(S) ![]() is in smoothness class
is in smoothness class
![]() ;
;
30pt
to 30pt(D) ![]() is one-dimensional;
is one-dimensional;
30pt
to 30pt(O) ![]() ,
, ![]() , is to be estimated.
, is to be estimated.
Then the lower rate of convergence is ![]() with
with
Stone (1982) proved that under the assumptions of this theorem the rate ![]() with
with ![]() as in 4.1.1 is also achievable in some weaker sense than
defined earlier. He also showed that for a suitable generalization of
as in 4.1.1 is also achievable in some weaker sense than
defined earlier. He also showed that for a suitable generalization of
![]() the optimal rate in this weaker sense is
the optimal rate in this weaker sense is ![]() with
with
Note that the optimal rate tends to zero faster if the regression curve
has more derivatives existing. The optimal rate tends to zero slower if
the ![]() -variable is of higher dimension or if higher order derivatives
-variable is of higher dimension or if higher order derivatives
![]() of
of ![]() are to be estimated.
are to be estimated.
Kernel estimators are asymptotically optimal if the bandwidth sequence and the
kernel function are suitably chosen. Consider the fixed design model in which
the data are taken at ![]() and
and
![]() , where
, where
![]() is normal with variance
is normal with variance ![]() .
Suppose that
.
Suppose that ![]() is four-times
differentiable and it is desired to estimate the second derivative
is four-times
differentiable and it is desired to estimate the second derivative ![]() .
.
Theorem 4.1.2 says that for this estimation problem
![]() the best
rate of convergence can only be
the best
rate of convergence can only be ![]() . If this rate is also achievable it
is optimal. In particular,
. If this rate is also achievable it
is optimal. In particular, ![]() is a lower rate of convergence. (Recall
the definition of optimal rate of convergence.) I shall show that the rate
is a lower rate of convergence. (Recall
the definition of optimal rate of convergence.) I shall show that the rate ![]() is achievable over
is achievable over
![]() for a certain kernel. Take the
Priestley-Chao kernel estimate with weight sequence
for a certain kernel. Take the
Priestley-Chao kernel estimate with weight sequence
![]() :
:
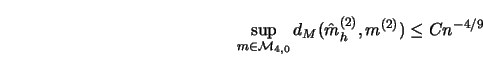
Note that if ![]() is chosen different from
is chosen different from ![]() , in this example the
kernel estimator will not achieve the optimal rate. To illustrate this,
consider a bandwidth sequence
, in this example the
kernel estimator will not achieve the optimal rate. To illustrate this,
consider a bandwidth sequence
![]() with
with ![]() positive or
negative. If
positive or
negative. If ![]() then the squared bias component of
then the squared bias component of
![]() dominates and
dominates and
![]() .
If
.
If ![]() then the variance component of
then the variance component of
![]() dominates and
dominates and
![]() . In any case, the rate of convergence
is slower than the optimal rate
. In any case, the rate of convergence
is slower than the optimal rate ![]() .
.
This example shows that it is very important to tune the smoothing parameter
![]() to the right speed to balance bias
to the right speed to balance bias![]() and variance. In Section
5.1 it
will be seen how data-driven bandwidths can be constructed which automatically
achieve the correct rate of convergence, giving asymptotically optimal
estimates. This might seem to be somewhat at odds with the merits of the
nonparametric smoothing approach. One motivated nonparametric regression
estimation by a desire to assume less about the structure of
and variance. In Section
5.1 it
will be seen how data-driven bandwidths can be constructed which automatically
achieve the correct rate of convergence, giving asymptotically optimal
estimates. This might seem to be somewhat at odds with the merits of the
nonparametric smoothing approach. One motivated nonparametric regression
estimation by a desire to assume less about the structure of ![]() than in a
parametric framework, but in order to construct optimal estimators one seems
to need the very specific assumption that higher derivatives up to certain
order exist. A way out of this dilemma is presented in Section
5.1 where it is
seen that the smoothing parameter can, in fact, be adapted to the degree of
smoothness of
than in a
parametric framework, but in order to construct optimal estimators one seems
to need the very specific assumption that higher derivatives up to certain
order exist. A way out of this dilemma is presented in Section
5.1 where it is
seen that the smoothing parameter can, in fact, be adapted to the degree of
smoothness of ![]() without prior knowledge of the degree of differentiability
of
without prior knowledge of the degree of differentiability
of ![]() .
.
On the other hand, the aim to achieve the optimal rate over a specific
smoothness class should not be taken too literally, since in a practical
situation the number
![]() , will not be much different
from
, will not be much different
from
![]() . Suppose that
. Suppose that ![]() . Even if we double
the degree of differentiability to achieve a better rate of convergence, the
relative improvement,
. Even if we double
the degree of differentiability to achieve a better rate of convergence, the
relative improvement,
![]() , for a sample size of
, for a sample size of ![]() is
only 3.5 percent.
is
only 3.5 percent.
Note that there are kernel smoothers of the form 4.1.3 which do not achieve
the optimal rate of ![]() . This addresses the fourth characteristic (T)
of regression smoothing: The type of estimator has to be selected in a
reasonable way in order to achieve the optimal rate. Suppose that we had taken
an asymmetric kernel in 4.1.3 which did not fulfill the orthogonality
condition
. This addresses the fourth characteristic (T)
of regression smoothing: The type of estimator has to be selected in a
reasonable way in order to achieve the optimal rate. Suppose that we had taken
an asymmetric kernel in 4.1.3 which did not fulfill the orthogonality
condition
![]() . A little calculus and partial integration
yields
. A little calculus and partial integration
yields
More general distance measures of the form
![\begin{displaymath}d_{L_\nu}\ ({\hat{m}},m)=\left[ \int \left\vert {\hat{m}}(x)-m(x) \right\vert ^\nu w(x) d x
\right]^{1/\nu},\quad \nu \ge 1,\end{displaymath}](anrhtmlimg958.gif)

Exercises
4.1.1 From the discussion after Theorem 4.1.2 we have seen that the
type of estimator has to be adapted as well to achieve the optimal rate of
convergence. Consider now the fixed design setting and ![]() and a
positive kernel weight sequence. Such a kernel smoother cannot achieve the
optimal rate which is
and a
positive kernel weight sequence. Such a kernel smoother cannot achieve the
optimal rate which is
[Hint: Compute the bias as in Section 3.1]
4.1.2 Conduct a small Monte Carlo study in which you compare the
distances ![]() and
and ![]() for the same bandwidth. Do you observe the
slower rate of convergence for
for the same bandwidth. Do you observe the
slower rate of convergence for ![]() ?
?
4.1.3 Describe the qualitative differences of the accuracy measures
![]() and
and ![]() .
.
[Hint: Consider a situation where the smooth curve contains a wild single spike or wiggles around the true curve with a small variation.]
4.1.4 Give exact arguments for 4.1.4 in the fixed design setting.
[Hint: Look up the paper by Gasser and Müller (1984).]
4.1.5 Compute the optimal bandwidth that minimizes the first two
dominant terms of MISE. Interpret the constants occurring in this
asymptotically optimal bandwidth. When will ![]() tend to be large? When would
you expect
tend to be large? When would
you expect ![]() to be small?
to be small?
4.1.6 Compute the bandwidth that balances the stochastic and the bias term for the supremum distance. Is it going faster or slower to zero than the MSE optimal bandwidth?
[Hint: The stochastic term is of order
![]() as is shown in the complements. The systematic bias term is as seen
above of the order
as is shown in the complements. The systematic bias term is as seen
above of the order ![]() for
for
![]() .]
.]
To have some insight into why the ![]() rate has this additional log
term consider the one-dimensional case
rate has this additional log
term consider the one-dimensional case ![]() . We have to estimate the
following probability.
. We have to estimate the
following probability.
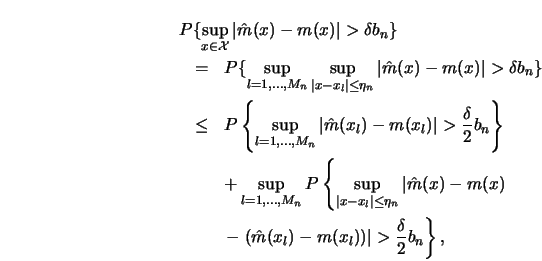
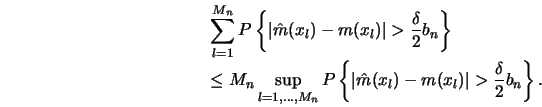
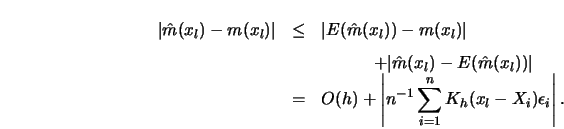
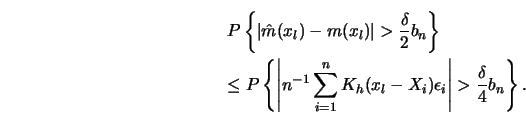
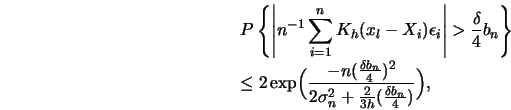
![\begin{displaymath}\sigma_n=E [h^{-2} K^2 (x_l-X_i)]=O(h^{-1}).\end{displaymath}](anrhtmlimg985.gif)