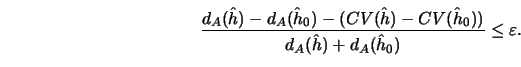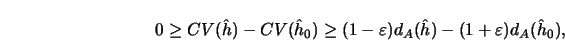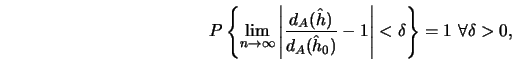The accuracy of kernel smoothers
as estimators of ![]() or of derivatives of
or of derivatives of
![]() is a function of the kernel
is a function of the kernel ![]() and the bandwidth
and the bandwidth ![]() . I have argued
that the accuracy depends mainly on the smoothing parameter
. I have argued
that the accuracy depends mainly on the smoothing parameter ![]() (Section
4.5). In this section, several bandwidth selection procedures will be
presented that optimize quadratic error measures for the regression curve
and its derivatives. In particular, I consider the distances
(Section
4.5). In this section, several bandwidth selection procedures will be
presented that optimize quadratic error measures for the regression curve
and its derivatives. In particular, I consider the distances
![\begin{eqnarray*}
d_A(h) &= &n^{-1} \sum^n_{j=1} [ \hat m_h(X_j)-m(X_j) ]^2 w(X_...
... w(x)f(x)dx, \cr
d_C(h) &=& E [ d_A(h)\vert X_1, \ldots, X_n ],
\end{eqnarray*}](anrhtmlimg1438.gif)
![\begin{displaymath}b^2(h)=n^{-1} \sum^n_{j=1} \left[ n^{-1} \sum^n_{i=1} W_{hi}(X_j)m(X_i)-
m(X_j) \right]^2 w(X_j)\end{displaymath}](anrhtmlimg1441.gif)
![\begin{displaymath}v(h)=n^{-1} \sum^n_{j=1} \left[ n^{-2} \sum^n_{i=1} W_{hi}(X_j) \sigma^2
(X_j) \right] w(X_j),\end{displaymath}](anrhtmlimg1442.gif)
The decreasing curve in Figure 5.1
shows ![]() roughly proportional to
roughly proportional to ![]() . The sum of both components
is the conditional squared error
. The sum of both components
is the conditional squared error ![]() , which is shown in Figure
5.1
as the curve above
, which is shown in Figure
5.1
as the curve above ![]() and
and ![]() .
.
![\includegraphics[scale=0.7]{ANRsimmbv.ps}](anrhtmlimg1456.gif)
|
![\includegraphics[scale=0.15]{ANR5,2.ps}](anrhtmlimg1463.gif)
|
Theorem 4.1.1 about the asymptotic equivalence of ![]() and
and ![]() states that all three distances should have roughly the same minimum. The
approximate identity of the three distances can be seen from Figure
5.2.
It is highly desirable to choose a smoothing parameter that balances
the systematic bias
states that all three distances should have roughly the same minimum. The
approximate identity of the three distances can be seen from Figure
5.2.
It is highly desirable to choose a smoothing parameter that balances
the systematic bias![]() effects versus the stochastic uncertainty
expressed by the magnitude of the variance. For such a choice of
smoothing parameter the squared bias and the variance are of the same order.
effects versus the stochastic uncertainty
expressed by the magnitude of the variance. For such a choice of
smoothing parameter the squared bias and the variance are of the same order.
How can we find such a smoothing parameter? We have already seen a
theoretical analysis of the MSE properties of kernel smoothers in Section
3.1. We know the asymptotic preferable choice of
![]() , but the MSE and thus
, but the MSE and thus ![]() involved complicated unknowns that had to be estimated from
the data as well.
involved complicated unknowns that had to be estimated from
the data as well.
The basic idea behind all smoothing parameter selection algorithms is to estimate the ASE or equivalent measures (up to some constant). The hope is then that the smoothing parameter minimizing this estimate is also a good estimate for the ASE itself. Expand the ASE as
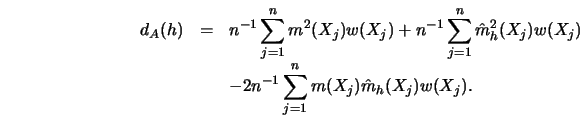
Can we estimate this expression (up to a constant)?
At first sight it seems possible.
The first term is independent of the smoothing parameter.
The second term can be computed entirely from the data. If
the third term could be estimated and if it vanished faster than ![]() itself tends to zero, then indeed a device for selecting the bandwidth
could be established quite easily.
itself tends to zero, then indeed a device for selecting the bandwidth
could be established quite easily.
A naive estimate of the third term would be

![\begin{displaymath}p(h)=n^{-1} \sum^n_{j=1} [ Y_j- \hat m_h(X_j) ]^2 w(X_j)\end{displaymath}](anrhtmlimg1471.gif)
![\includegraphics[scale=0.7]{ANRsimpre.ps}](anrhtmlimg1475.gif)
|
The intuitive reason for the bias in ![]() is that the
observation
is that the
observation ![]() is used (in
is used (in ![]() ) to predict itself. To see
this in more detail, consider the expansion
) to predict itself. To see
this in more detail, consider the expansion
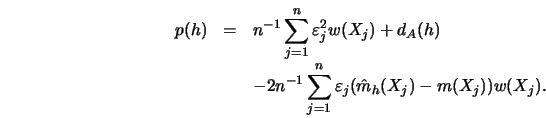
![\begin{displaymath}-2n^{-1} \sum^n_{j=1} [ n^{-1} W_{hj}(X_j) \sigma^2 (X_j) ] w(X_j).
\end{displaymath}](anrhtmlimg1480.gif)
The leave-out method is based on regression smoothers
in which one, say the ![]() th, observation is left out:
th, observation is left out:
The function ![]() is commonly called a
cross-validation function since
it validates the ability to predict
is commonly called a
cross-validation function since
it validates the ability to predict
![]() across the
subsamples
across the
subsamples
![]() (Stone 1974).
In the context of
kernel smoothing this score function for finding
(Stone 1974).
In the context of
kernel smoothing this score function for finding ![]() was
proposed by Clark (1975). The idea is related to variables selection in
linear regression. Allen (1974) proposed the related quantity
PRESS (prediction sum of
squares). Wahba and Wold (1975) proposed a similar technique in the
context of spline smoothing. The general structure of smoothing methods
in linear regression models is discussed in Hall and Titterington (1986a).
was
proposed by Clark (1975). The idea is related to variables selection in
linear regression. Allen (1974) proposed the related quantity
PRESS (prediction sum of
squares). Wahba and Wold (1975) proposed a similar technique in the
context of spline smoothing. The general structure of smoothing methods
in linear regression models is discussed in Hall and Titterington (1986a).
The reason why
cross-validation works is simple: The cross-product term
from the ![]() function,
similar to 5.1.1, is
function,
similar to 5.1.1, is
![\includegraphics[scale=0.7]{ANRsimcv.ps}](anrhtmlimg1489.gif)
|
Note that by itself
the fact that 5.1.4 has expectation zero does not
guarantee that
![]() minimizes
minimizes ![]() (or any other
of the equivalent error measures). For this procedure it must be required
that
(or any other
of the equivalent error measures). For this procedure it must be required
that ![]() converges uniformly over
converges uniformly over ![]() to zero.
Note also that the bandwidth suggested here by cross-validation (for the
quartic kernel,
to zero.
Note also that the bandwidth suggested here by cross-validation (for the
quartic kernel, ![]() ) is not exactly equal to the subjectively chosen
bandwidth from Section 3.11. The reason may be twofold. First, the two
bandwidths could be really different, even on the ``correct scale."
Second, they could be different since Figure 3.21 was produced with a
Gaussian kernel and the above cross-validation function was computed
using a quartic kernel. A ``common scale" for comparing bandwidths
from different kernels is derived in Section 5.4.
) is not exactly equal to the subjectively chosen
bandwidth from Section 3.11. The reason may be twofold. First, the two
bandwidths could be really different, even on the ``correct scale."
Second, they could be different since Figure 3.21 was produced with a
Gaussian kernel and the above cross-validation function was computed
using a quartic kernel. A ``common scale" for comparing bandwidths
from different kernels is derived in Section 5.4.
The second proposal, based on adjusting
![]() in a suitable way, aims at an
asymptotic cancellation of the bias 5.1.1. For this purpose
introduce the penalizing
function
in a suitable way, aims at an
asymptotic cancellation of the bias 5.1.1. For this purpose
introduce the penalizing
function ![]() with first-order Taylor expansion
with first-order Taylor expansion
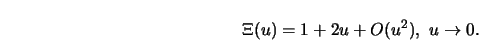
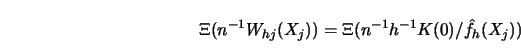
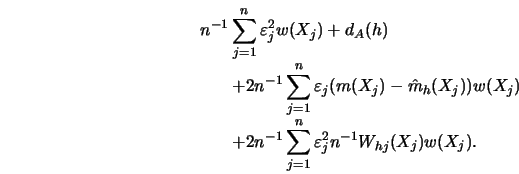
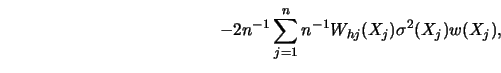

The third method, the ``plug-in" procedure, is based on the asymptotic expansion of the squared error for kernel smoothers:
![\begin{eqnarray*}
MSE &=& n^{-1} h^{-1} \sigma^2(x) c_K/f(x) \cr
&& + h^4 [ d_K (m''(x)+2m'(x) (f'/f)(x) )/2 ]^2.
\end{eqnarray*}](anrhtmlimg1507.gif)
The first two methods, the leave-out and the penalty technique, lead to
estimates of ![]() (up to a shift of
(up to a shift of ![]() ) and hence to
estimates of
) and hence to
estimates of ![]() . The random constant by which the
. The random constant by which the ![]() function
or the
function
or the ![]() function differ from
function differ from ![]() is roughly
is roughly
![]() , which tends to
, which tends to
![]() . In Figure 5.5, the upper curve is the
. In Figure 5.5, the upper curve is the ![]() -function and the
lower curve, with a similar shape is the averaged squared error
-function and the
lower curve, with a similar shape is the averaged squared error ![]() for
the simulation example (Table 2, Appendix 2).
for
the simulation example (Table 2, Appendix 2).
![\includegraphics[scale=0.7]{ANRsimcvase.ps}](anrhtmlimg1512.gif)
|
The two curves in Figure 5.5 differ by a constant in the
range ![]() , which is a
remarkably accurate estimate of
, which is a
remarkably accurate estimate of
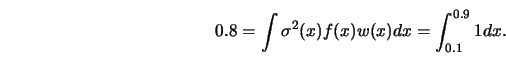
Consider the example of finding the Engel curve of potatoes as a function
of net income.
Figure 1.1 shows the data in the form of a sunflower plot. The
cross-validation curve ![]() of this data set is
displayed in Figure 5.6.
of this data set is
displayed in Figure 5.6.
![\includegraphics[scale=0.15]{ANR5,6.ps}](anrhtmlimg1519.gif)
|
The cross-validation function has a clear minimum at
![]() .
The corresponding kernel smooth is shown in Figure 5.7.
.
The corresponding kernel smooth is shown in Figure 5.7.
![\includegraphics[scale=0.7]{ANRpotqua.ps}](anrhtmlimg1523.gif)
|
The estimated curve shows the same nonlinearity as Figure 1.2 but is slightly rougher.
In order to make cross-validation or the penalty method a mathematically
justifiable device for selecting the smoothing parameter, it must be
shown that the score (![]() or
or ![]() ) approximates (up to a constant)
the accuracy measure
) approximates (up to a constant)
the accuracy measure ![]() uniformly over
uniformly over ![]() .
If this is the case,
then the relative loss for a selected bandwidth
.
If this is the case,
then the relative loss for a selected bandwidth ![]() ,
,
30pt
to 30pt(A1) for ![]() ,
,
![]() ,
where
,
where
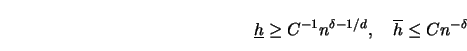
30pt
to 30pt(A2) ![]() is Hölder continuous, that is, for some
is Hölder continuous, that is, for some ![]() ,
,
![]()
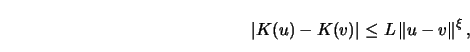

30pt
to 30pt(A3) the regression function ![]() and the marginal density
and the marginal density ![]() are Hölder continuous;
are Hölder continuous;
30pt
to 30pt(A4)
the conditional moments of ![]() given
given ![]() are bounded in
the sense that there are positive constants
are bounded in
the sense that there are positive constants
![]() such that for
such that for
![]() ,
,
![]() for all
for all ![]() ;
;
30pt
to 30pt(A5) the marginal density ![]() of
of ![]() is bounded from below
on the support of
is bounded from below
on the support of ![]() ;
;
30pt
to 30pt(A6)
the marginal density ![]() of
of ![]() is compactly supported.
is compactly supported.
Then the bandwidth selection rule, ``Choose ![]() to
minimize
to
minimize ![]() (
(![]() ) (or
) (or ![]() (
(![]() ))" is asymptotically optimal.
))" is asymptotically optimal.
Asymptotic optimality
of the kernel smoother with weights
![]() was shown
by Härdle and Kelly (1987) for a slightly larger range of bandwidths.
Rice (1984a)
proved a related theorem using penalizing functions
in the fixed design setting.
These penalizing functions do not yield asymptotically optimal smoothing
parameters in the stochastic design setting,
as was shown by Härdle and Marron (1985a).
was shown
by Härdle and Kelly (1987) for a slightly larger range of bandwidths.
Rice (1984a)
proved a related theorem using penalizing functions
in the fixed design setting.
These penalizing functions do not yield asymptotically optimal smoothing
parameters in the stochastic design setting,
as was shown by Härdle and Marron (1985a).
It is remarkable that the above devices yield optimal smoothing
parameters without reference to a specific smoothness class to which
either ![]() or
or ![]() belongs. Minimization of
belongs. Minimization of ![]() is performed over a
wide range
is performed over a
wide range ![]() of possible bandwidths. The method is not just
restricted to a specific range, for example,
of possible bandwidths. The method is not just
restricted to a specific range, for example,
![]() containing, for example, the optimal smoothing parameters for
twice differentiable regression functions. In this sense, the
cross-validation
and the penalty method yield optimal smoothing parameters
uniformly over smoothness classes (see the remarks of Section 4.1).
This, in turn, has
the effect that the data-driven kernel smoothers achieve ``their" optimal
rate, independently of the smoothness of the underlying regression model
(Härdle and Marron 1985b, section 3).
From a practical point of view, this last theoretical property of
cross-validated bandwidth sequences is welcome. The user of the
cross-validation method need not worry about the roughness of
the underlying curve. The cross-validated bandwidth will
automatically give him the right amount of smoothing, independently of
how smooth (in terms of degree of differentiability) the true regression
curve is. This feature is not accomplished by the ``plug-in" method.
containing, for example, the optimal smoothing parameters for
twice differentiable regression functions. In this sense, the
cross-validation
and the penalty method yield optimal smoothing parameters
uniformly over smoothness classes (see the remarks of Section 4.1).
This, in turn, has
the effect that the data-driven kernel smoothers achieve ``their" optimal
rate, independently of the smoothness of the underlying regression model
(Härdle and Marron 1985b, section 3).
From a practical point of view, this last theoretical property of
cross-validated bandwidth sequences is welcome. The user of the
cross-validation method need not worry about the roughness of
the underlying curve. The cross-validated bandwidth will
automatically give him the right amount of smoothing, independently of
how smooth (in terms of degree of differentiability) the true regression
curve is. This feature is not accomplished by the ``plug-in" method.
The cross-validation procedure is formally described in the following algorithm.
DO OVER (a dense grid ![]() of
of ![]() values)
values)
STEP 1.
Compute the leave-out estimate

STEP 2.
Construct the cross validation function
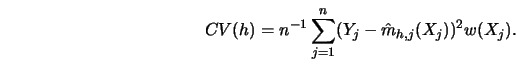
END OVER.
STEP 3.
Define the automatic bandwidth as
![\begin{displaymath}\hat h = \arg\min_{h \in H_n } [CV(h)]\end{displaymath}](anrhtmlimg1544.gif)
The principal idea for smoothing parameter selection in the setting of
derivative estimation is similar to that of finding a bandwidth for
estimating ![]() itself. As in Rice (1985), consider the setting of
fixed, equidistant predictor variables.
The
leave-out estimators for estimating
itself. As in Rice (1985), consider the setting of
fixed, equidistant predictor variables.
The
leave-out estimators for estimating ![]() are defined by leaving out the
observations
are defined by leaving out the
observations ![]() and
and
![]()
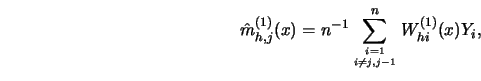
![\begin{displaymath}CV^{(1)} (h)=n^{-1}_2 \sum^{n_2}_{j=1} [ Y^{(1)}_{(2j)} - \hat
m^{(1)}_{h,(2j)} (X_{(2j)}) ]^2 w(X_{(2j)} ),\end{displaymath}](anrhtmlimg1550.gif)
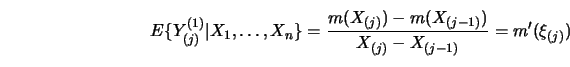
![\begin{eqnarray*}
\lefteqn{n^{-1}_2 \sum^{n_2}_{j=1} [ Y^{(1)}_{(j)}-m'(\xi_{(j)...
... [ m'
(\xi_{(j)}) -\hat m^{(1)}_{h,(j)} (X_{(j)}) ] w(X_{(j)}).
\end{eqnarray*}](anrhtmlimg1556.gif)
![\begin{eqnarray*}
\lefteqn {n^{-1}_2
\sum^{n_2}_{j=1} [ m'(\xi_{(j)})- \hat m_{...
...n_2}_{j=1} [
m'(X_{(j)})-\hat m^{(1)}_h (X_{(j)}) ]^2 w(X_{(j)}) \end{eqnarray*}](anrhtmlimg1557.gif)
![\begin{eqnarray*}
MSE &\approx & n^{-1}h^{-(2k+1)} \sigma^2
\int {K^{(k)}}^2(u...
... h^{p-k} m^{(k)}(x) (-1)^p \int u^p K^{(k)}(u)
du/p! \right]^2.
\end{eqnarray*}](anrhtmlimg1561.gif)
![\begin{displaymath}h_0^{(k)} = \left[ { 2k+1 \over 2(p-k) }
{ \sigma^2 \int {K...
...{m^{(k)}}^2(x)dx }
\right]^{ 1/(2p+1) } n^{ -1/(2p+1) }\cdotp \end{displaymath}](anrhtmlimg1562.gif)
![\begin{displaymath}C_{0,k} = \left[ { (2k+1)p \over p-k }
{ \int {K^{(k)}}^2(u)...
...-1)^p \int u^p K^{(k)}(u) du/p!]^2 }
\right]^{1/(2p+1)}\cdotp \end{displaymath}](anrhtmlimg1563.gif)

The weight function ![]() was introduced to reduce boundary effects. If one
had not introduced the weight function and just formed the bandwidth
selection scores over the whole data range one would have
obtained a bandwidth
sequence optimized with respect to the ``boundary behavior" of the
kernel smoother. As pointed out in Section 4.4, the convergence rate is
slightly slower at the boundary points. Since the cross-validation
method,
for example, is still asymptotically optimal (in the sense of
Theorem 5.1.1) one would artificially select a slower rate of convergence
in the center of the data range, where the majority of the data lie.
was introduced to reduce boundary effects. If one
had not introduced the weight function and just formed the bandwidth
selection scores over the whole data range one would have
obtained a bandwidth
sequence optimized with respect to the ``boundary behavior" of the
kernel smoother. As pointed out in Section 4.4, the convergence rate is
slightly slower at the boundary points. Since the cross-validation
method,
for example, is still asymptotically optimal (in the sense of
Theorem 5.1.1) one would artificially select a slower rate of convergence
in the center of the data range, where the majority of the data lie.
However, cutting the range of interest down to, say, 90 percent,
doesn't solve the problem since typically the kernel weights cover more
than 10 percent of the data range (see Figure 5.6). This raises
the question of how variable the ![]() -function is as the weight function
-function is as the weight function
![]() is varied. Figure 5.8 shows an optimal kernel smooth estimating
liver weights as a function of age. The
is varied. Figure 5.8 shows an optimal kernel smooth estimating
liver weights as a function of age. The ![]() -function was computed
disregarding the outer 5 percent data on each side.
What happens if the weight function
-function was computed
disregarding the outer 5 percent data on each side.
What happens if the weight function ![]() is varied?
is varied?
Figure 5.9 shows cross-validation curves as the weights cut off 2, 4, 6, 8 and 10 percent of the data at each end of the data interval. The location of the minimum, the selected optimal bandwidth, is remarkably stable except for the case where only 80 percent of the data interval is cross-validated. I did similar comparisons for the simulated data set (Table 2, Appendix 2) and found qualitatively the same behavior: The weight function does not influence the selected bandwidth to a large extent.
![\includegraphics[scale=0.15]{ANR5,8.ps}](anrhtmlimg1566.gif)
|
![\includegraphics[scale=0.15]{ANR5,9.ps}](anrhtmlimg1569.gif)
|
Exercises
5.1.1Try cross validation and some of the penalizing functions to find a smoothing
parameter for the simulated data set given
in the appendix.
5.1.2Recall the asymptotic equivalence of ![]() -
-![]() and kernel smoothing. How would you
choose a good
and kernel smoothing. How would you
choose a good ![]() with the cross validation method?
with the cross validation method?
5.1.3How would you modify the penalizing functions in the setting of ![]() -
-![]() smoothing?
smoothing?
5.1.4Write an efficient algorithm for computing the cross validation function.
[Hint: Use the WARPing technique or the FFT method.]
5.1.5One could argue that an asymptotically optimal smoothing parameter for ![]() is
also good for estimating
is
also good for estimating ![]() . A good estimate for
. A good estimate for ![]() should give a good
estimate for
should give a good
estimate for ![]() ! Can you find an argument against this?
! Can you find an argument against this?
5.1.6Find
![]() and
and
![]() .
Compare
.
Compare ![]() with
with ![]() . Do you find that
. Do you find that
![]() ?
[Hint: Study the factor method. ]
?
[Hint: Study the factor method. ]
Proof of Theorem 5.1.1
The proof of this theorem is based on the uniform approximation (over
![]() ) of the distances
) of the distances ![]() , and so on; see Theorem
4.1.1. If
suffices to prove the asymptotic optimality for
, and so on; see Theorem
4.1.1. If
suffices to prove the asymptotic optimality for ![]() .
The Hölder continuity of
.
The Hölder continuity of ![]() ensures that it suffices to consider a
discrete subset
ensures that it suffices to consider a
discrete subset ![]() of
of ![]() .
The existence
of all conditional moments of order
.
The existence
of all conditional moments of order ![]() gives over this sufficiently
dense subset
gives over this sufficiently
dense subset ![]() of
of ![]() :
:
![\begin{displaymath}
% latex2html id marker 14464
\hat h_0 = \mathop {\arg\min}_{h \in H_n} [d_A(h)],\end{displaymath}](anrhtmlimg1580.gif)
![\begin{displaymath}
% latex2html id marker 14466
\hat h= \mathop {\arg\min}_{h \in H_n} [CV(h)].\end{displaymath}](anrhtmlimg1581.gif)