We have already encountered a straightforward
resistant technique: median smoothing. It
is highly robust since the extreme response observations (stemming from
predictor variables in a neighborhood
around ![]() ) do not have any effect on
the (local) median of the response
variables. A slight disadvantage of median smoothing, though, is that it
produces a rough and wiggly curve. Resmoothing and twicing
are data-analytic techniques to ameliorate median smoothing in this respect; see
Velleman (1980) and Mallows (1980).
) do not have any effect on
the (local) median of the response
variables. A slight disadvantage of median smoothing, though, is that it
produces a rough and wiggly curve. Resmoothing and twicing
are data-analytic techniques to ameliorate median smoothing in this respect; see
Velleman (1980) and Mallows (1980).
Cleveland (1979) proposed the following algorithm, LOWESS,
a resistant method based on local polynomial fits. The basic idea is to start
with a local polynomial least squares fit and then to ``robustify" it.
``Local" means here a ![]() -
-![]() type neighborhood.
The procedure starts from a
type neighborhood.
The procedure starts from a ![]() -
-![]() pilot estimate and iteratively defines
robustness weights and re-smoothes several times.
pilot estimate and iteratively defines
robustness weights and re-smoothes several times.
LOWESS
STEP 1.
Fit a polynomial regression in a neighborhood
of ![]() , that is, find
coefficients
, that is, find
coefficients
![]() which minimize
which minimize
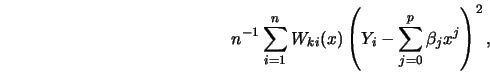
FOR ![]() TO maxiter DO BEGIN
TO maxiter DO BEGIN
STEP 2.
Compute from the estimated residuals
![]() the scale estimate
the scale estimate
![]() med
med
![]() and define robustness weights
and define robustness weights
![]() , where
, where ![]() denotes the quartic kernel,
denotes the quartic kernel,
![]() .
.
STEP 3.
Fit a polynomial regression as in STEP 1
but with weights

Cleveland recommends the choice ![]() (as for the supersmoother )
as striking
a good balance between computational ease and the need for
flexibility to reproduce patterns in the data. The smoothing parameter
can be determined by cross-validation as in Section 5.1.
Figure 6.2 shows an application of Cleveland's algorithm to a
simulated data set. It is quite obvious that the LOWESS smooth is resistant
to the ``far out" response variables at the upper borderline of the plot.
(as for the supersmoother )
as striking
a good balance between computational ease and the need for
flexibility to reproduce patterns in the data. The smoothing parameter
can be determined by cross-validation as in Section 5.1.
Figure 6.2 shows an application of Cleveland's algorithm to a
simulated data set. It is quite obvious that the LOWESS smooth is resistant
to the ``far out" response variables at the upper borderline of the plot.
![\includegraphics[scale=0.2]{ANR6,2.ps}](anrhtmlimg1859.gif)
|
Another class of resistant smoothers is given by local trimmed
averages of the response variables. If
![]() denotes the order statistic from
denotes the order statistic from ![]() observations
observations
![]() ,
a trimmed average (mean) is defined by
,
a trimmed average (mean) is defined by
![\begin{displaymath}\overline Z_{\alpha} = (N-2
[ \alpha N ])^{-1} \sum^{N - [ \alpha N ]}_{j= [
\alpha N ]} Z_{(j)}, 0<\alpha<1/2,\end{displaymath}](anrhtmlimg1862.gif)
![]() -smoothing is a resistant technique:
the ``far out extremes" at a point
-smoothing is a resistant technique:
the ``far out extremes" at a point ![]() do not enter
the local averaging procedure. More generally, one considers a
conditional
do not enter
the local averaging procedure. More generally, one considers a
conditional ![]() -functional
-functional
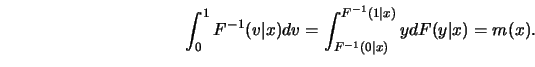
In practice, we do not know
![]() and we have to estimate it.
If
and we have to estimate it.
If
![]() denotes an estimator of
denotes an estimator of
![]() one obtains from formula
6.1.1
the
one obtains from formula
6.1.1
the ![]() -smoothers. Estimates of
-smoothers. Estimates of ![]() can be
constructed, for example, by the kernel technique,
can be
constructed, for example, by the kernel technique,
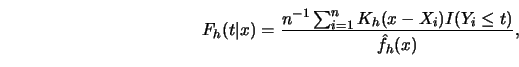
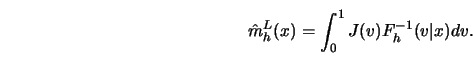
Yet another class of smoothers are the ![]() -smoothers derived from
-smoothers derived from
![]() -estimates of location.
Assume that
-estimates of location.
Assume that
![]() is symmetric around
is symmetric around
![]() and that
and that ![]() is a nondecreasing function defined on
is a nondecreasing function defined on ![]() such that
such that
![]() . Then the score
. Then the score
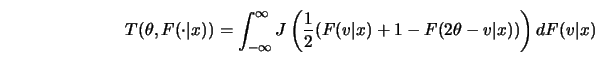
Consider a two-sample rank test for shift based on the sample
![]() and
and
![]() , that is, a mirror image of the
first sample serves as a stand-in for the second sample. Now try
to adjust
, that is, a mirror image of the
first sample serves as a stand-in for the second sample. Now try
to adjust ![]() in such a way that the test statistic
in such a way that the test statistic
![]() based on the scores
based on the scores
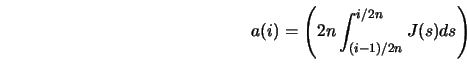
A solution of
![]() is, in general, not unique or may have irregular behavior. Cheng
and Cheng (1986) therefore suggested
is, in general, not unique or may have irregular behavior. Cheng
and Cheng (1986) therefore suggested
Resistant smoothing techniques based on ![]() -estimates of location are
called
-estimates of location are
called ![]() -smoothers .
Recall that all smoothers of the
form
-smoothers .
Recall that all smoothers of the
form

In the setting of spline smoothing,
an ![]() -type spline was defined by Cox(1983)
-type spline was defined by Cox(1983)
Kernel smoothers can be made resistant by similar means. Assume that the
conditional distribution
![]() is symmetric. This assumption
ensures that we are still estimating
is symmetric. This assumption
ensures that we are still estimating ![]() , the conditional mean curve.
Define a robust kernel
, the conditional mean curve.
Define a robust kernel
![]() -smoother
-smoother ![]() as
as


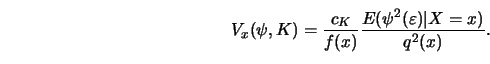
This result deserves some discussion. First, it shows that kernel
![]() -smoothers can be interpreted as ordinary kernel smoothers
applied to
nonobservable pseudo-data
with transformed errors
-smoothers can be interpreted as ordinary kernel smoothers
applied to
nonobservable pseudo-data
with transformed errors
![]() .
This sheds some light on how the resistance of
.
This sheds some light on how the resistance of
![]() -smoothers is achieved: The ``extreme" observation errors
-smoothers is achieved: The ``extreme" observation errors
![]() are ``downweighted" by the nonlinear,
bounded function
are ``downweighted" by the nonlinear,
bounded function
![]() . Second, Theorem 6.1.1 reveals that the bias of the
ordinary kernel smoother is the same as that for the kernel
. Second, Theorem 6.1.1 reveals that the bias of the
ordinary kernel smoother is the same as that for the kernel ![]() -smoother.
The nonlinear definition of
-smoother.
The nonlinear definition of ![]() does not affect the (asymptotic)
bias properties. Third, the product form of the asymptotic variance
does not affect the (asymptotic)
bias properties. Third, the product form of the asymptotic variance ![]() as a product of
as a product of ![]() and
and
![]() allows optimization
of
allows optimization
of ![]() simply by considering
simply by considering ![]() and
and ![]() separately.
separately.
The first of these two separate problems was
solved in Section 4.5.
By utilizing classical theory for
![]() -estimates of location, the second problem can be treated as in Huber
(1981, chapter 4). The details of this
optimization technique are rather delicate; the reader is referred
to the standard literature on robust estimation. Optimization of the
smoothing parameter is discussed in Härdle (1984c) and more recently by
Leung (1988). Both authors consider the direct analogue of cross-validation,
namely, construct robust leave-one-out smoothers and then to proceed as
in Section 5.1.
-estimates of location, the second problem can be treated as in Huber
(1981, chapter 4). The details of this
optimization technique are rather delicate; the reader is referred
to the standard literature on robust estimation. Optimization of the
smoothing parameter is discussed in Härdle (1984c) and more recently by
Leung (1988). Both authors consider the direct analogue of cross-validation,
namely, construct robust leave-one-out smoothers and then to proceed as
in Section 5.1.
A natural question to ask is, how much is gained or lost in asymptotic
accuracy when using an ![]() -smoother? The bias is the same
as for the kernel smoother. A way of comparing the
nonresistant and the resistant technique is therefore to study the ratio of
asymptotic variances,
-smoother? The bias is the same
as for the kernel smoother. A way of comparing the
nonresistant and the resistant technique is therefore to study the ratio of
asymptotic variances,
As an example, I would like to present a smoothing problem in physical chemistry. Raman spectra are an important diagnostic tool in that field. One would like to identify the location and size of peaks and troughs of spectral bands; see Hillig and Morris (1982) and Bussian and Härdle (1984). Unfortunately, small-scale instrumental noise and a certain proportion of observation error which is caused by random external events blur the observations. The latter type of error causes high frequency signals or bubbles in the sample and produces single spikes like those in Figure 6.3.
![\includegraphics[scale=0.3]{ANR6,3.ps}](anrhtmlimg1922.gif)
|
Estimating with ![]() the ordinary Nadaraya-Watson kernel
smoother, results in the curve depicted in Figure 6.4.
the ordinary Nadaraya-Watson kernel
smoother, results in the curve depicted in Figure 6.4.
![\includegraphics[scale=0.3]{ANR6,4.ps}](anrhtmlimg1926.gif)
|
The single spike outliers obviously produced two spurious neighboring peaks. The resistant smoothing technique, on the other hand, leads to Figure 6.5.
![\includegraphics[scale=0.3]{ANR6,5.ps}](anrhtmlimg1929.gif)
|
The influence of the outliers is obviously reduced.
Uniform confidence bands -- based on asymptotic extreme value theory --
may be constructed using the methods presented in
Section 4.3; see Härdle (1987b).
Figure 6.6 depicts a kernel ![]() -smoother
-smoother ![]() together with uniform confidence bands, and
together with uniform confidence bands, and ![]() , the
Nadaraya-Watson kernel smoother, for the data presented in Figure
6.1.
, the
Nadaraya-Watson kernel smoother, for the data presented in Figure
6.1.
![\includegraphics[scale=0.15]{ANR6,6.ps}](anrhtmlimg1931.gif)
|
Optimal uniform convergence rates (see Section 4.1) for kernel
![]() -smoothers have been derived in Härdle and Luckhaus (1984). In the
context of time series, robust estimation and prediction has been discussed
by Velleman (1977, 1980), Mallows (1980) and Härdle and Tuan (1986).
Robust nonparametric
prediction of time series by
-smoothers have been derived in Härdle and Luckhaus (1984). In the
context of time series, robust estimation and prediction has been discussed
by Velleman (1977, 1980), Mallows (1980) and Härdle and Tuan (1986).
Robust nonparametric
prediction of time series by ![]() -smoothers has been investigated by
Robinson (1984, 1987b), Collomb and Härdle (1986) and Härdle (1986c).
Robust kernel smoothers for estimation of derivatives have been
investigated in Härdle and Gasser (1985) and Tsybakov (1986).
-smoothers has been investigated by
Robinson (1984, 1987b), Collomb and Härdle (1986) and Härdle (1986c).
Robust kernel smoothers for estimation of derivatives have been
investigated in Härdle and Gasser (1985) and Tsybakov (1986).
Exercises
6.1.1
Find conditions such that ![]() -smoothers, as defined in 6.1.1,
are consistent estimators for the regression curve.
-smoothers, as defined in 6.1.1,
are consistent estimators for the regression curve.
6.1.2
Find conditions such that ![]() -smoothers, as defined in 6.1.2,
asymptotically converge to the true regression curve.
-smoothers, as defined in 6.1.2,
asymptotically converge to the true regression curve.
6.1.3
Do you expect the general ![]() -smoothers 6.1.1 to produce smoother curves
than the running median?
-smoothers 6.1.1 to produce smoother curves
than the running median?
6.1.4
Construct a fast algorithm for ![]() -smoothers 6.1.1. Based on the ideas of
efficent running median smoothing (Section 3.8) you should be able to find a
code that runs in
-smoothers 6.1.1. Based on the ideas of
efficent running median smoothing (Section 3.8) you should be able to find a
code that runs in ![]() steps (
steps (![]() is the number of neighbors).
is the number of neighbors).
6.1.5
Prove consistency for the ![]() -smoother 6.1.4 for monotone
-smoother 6.1.4 for monotone ![]() functions.
functions.
[Hint: Follow the proof of Huber (1981, chapter 3).]
6.1.6
Can you extend the proof of Exercise 6.1.4 to nonmonotone ![]() functions
such as Hampels ``three part redescender?"
functions
such as Hampels ``three part redescender?"