



Next: 7.2 Model Characteristics
Up: 7. Generalized Linear Models
Previous: 7. Generalized Linear Models
7.1 Introduction
Generalized linear models (GLM) extend the concept of the
well understood linear regression model.
The linear model assumes that the conditional expectation of 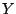 (the dependent or response variable) is equal to
a linear combination
(the dependent or response variable) is equal to
a linear combination
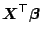 , i.e.
, i.e.
This could be equivalently written as
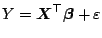 .
Unfortunately, the restriction to linearity cannot take into account a variety of
practical situations. For example, a continuous distribution of the
error
.
Unfortunately, the restriction to linearity cannot take into account a variety of
practical situations. For example, a continuous distribution of the
error
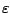 term implies that the response
term implies that the response 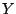 must have a continuous
distribution as well. Hence, the linear regression model
may fail when dealing with binary
must have a continuous
distribution as well. Hence, the linear regression model
may fail when dealing with binary 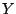 or with counts.
or with counts.
Example 1 (Bernoulli
responses)
Let us illustrate a binary response model (Bernoulli 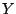 ) using a sample
on credit worthiness. For each individual in the sample we know
if the granted loan has defaulted or not. The responses are coded as
The term of interest is how credit worthiness depends on
observable individual characteristics
) using a sample
on credit worthiness. For each individual in the sample we know
if the granted loan has defaulted or not. The responses are coded as
The term of interest is how credit worthiness depends on
observable individual characteristics
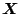 (age, amount and duration
of loan, employment, purpose of loan, etc.).
Recall that for a Bernoulli variable
(age, amount and duration
of loan, employment, purpose of loan, etc.).
Recall that for a Bernoulli variable
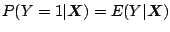 holds. Hence, the default probability
holds. Hence, the default probability
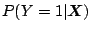 equals a regression of
equals a regression of 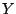 on
on
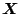 . A useful approach
is the following logit model:
Here the function of interest
. A useful approach
is the following logit model:
Here the function of interest
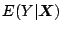 is linked to a linear function
of the explanatory variables by the logistic cumulative distribution
function (cdf)
is linked to a linear function
of the explanatory variables by the logistic cumulative distribution
function (cdf)
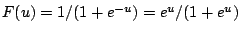 .
.
The term generalized linear models (GLM) goes back to
[29] and [27] who show that if the
distribution of the dependent variable 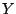 is a member of the
exponential family,
then the class of models which connects
the expectation of
is a member of the
exponential family,
then the class of models which connects
the expectation of 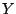 to a linear combination of the variables
to a linear combination of the variables
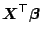 can be treated in a unified way.
In the following sections we denote the function which relates
can be treated in a unified way.
In the following sections we denote the function which relates
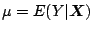 and
and
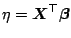 by
by
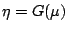 or
or
This function 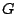 is called link function. For all
considered distributions of
is called link function. For all
considered distributions of 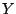 there exists at least one
canonical link function and typically a set of frequently
used link functions.
there exists at least one
canonical link function and typically a set of frequently
used link functions.




Next: 7.2 Model Characteristics
Up: 7. Generalized Linear Models
Previous: 7. Generalized Linear Models
![]() (the dependent or response variable) is equal to
a linear combination
(the dependent or response variable) is equal to
a linear combination
![]() , i.e.
, i.e.
![$\displaystyle Y=\left\{\begin{array}{ll}
1 & \quad \textrm{loan defaults},\\ [-1mm]
0 & \quad \textrm{otherwise}.
\end{array}\right.$](img4547.gif)
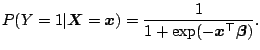
![]() is a member of the
exponential family,
then the class of models which connects
the expectation of
is a member of the
exponential family,
then the class of models which connects
the expectation of ![]() to a linear combination of the variables
to a linear combination of the variables
![]() can be treated in a unified way.
In the following sections we denote the function which relates
can be treated in a unified way.
In the following sections we denote the function which relates
![]() and
and
![]() by
by
![]() or
or