Définition 25
Soient
E et
F deux espaces vectoriels sur un corps
K. Une application
f de
E dans
F
est une application linéaire si et seulement si elle satisfait les deux conditions :
- 1.
- quels que soient les vecteurs u et v de E,
f(u+v)=f(u)+f(v)
- 2.
- quels que soient l'élément
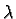 du corps K et le vecteur u de E,
du corps K et le vecteur u de E,
Si de plus
f est bijective, on dit que
f est un isomorphisme d'espaces vectoriels.
Proposition 9 (Caractérisation des applications linéaires)
Une application
f de
E dans
F est linéaire si et seulement si, quels que soient les
éléments
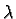
et
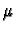
de
K et quels que soient les vecteurs
u et
v de
E
Preuve
- 1.
- Si f est linéaire alors
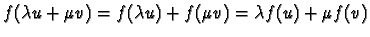 .
.
- 2.
- Réciproquement, si
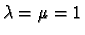 alors
f(u+v)=f(u)+f(v)
alors
f(u+v)=f(u)+f(v)
et si 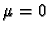 alors
alors
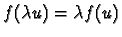 .
.
Remarque 14
- 1.
- L'application de R dans R définie par f(x)=x2 n'est pas linéaire :
- 2.
- On dispose ainsi de plusieurs possibilités pour calculer f(u+v) : soit on calcule la somme de
u et v dans E puis son image par f dans F, soit on calcule les images de u et v
dans F et on effectue leur somme dans ce dernier.
Soit f un isomorphisme d'espaces vectoriels. Montrer que l'application réciproque f-1 de
f est aussi une application linéaire (donc un isomorphisme).
Notations :
- 1.
- L'ensemble des applications linéaires de E dans F est noté LK(E,F) (ou L(E,F) s'il
n'y a pas d'ambiguité sur le corps K).
- 2.
- On note
L(E,E) = End(E) l'ensemble des endomorphismes de E
et Aut(E) l'ensemble des automorphismes de E (endomorphismes bijectifs de E).
Exemples
- 1.
- L'application nulle, l'identité, la multiplication par un scalaire et l'addition de deux vecteurs
sont des endomorphismes d'un espace vectoriel E.
- 2.
- Dans le plan, les rotations, les projections et les symétries sont des endomorphismes (et
même des automorphismes pour les rotations et symétries.)
- 3.
- L'application qui à un polynôme P fait correspondre son polynôme dérivé est un
endomorphisme (mais pas un automorphisme !) de l'espace vectoriel des polynômes à une
indéterminée.
Proposition 10
LK(
E,
F) est un K-espace vectoriel pour les lois suivantes
- 1.
- f+g :
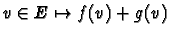
- 2.
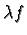 :
:
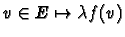
Montrer que si E, F et G sont 3 K-e.v.,
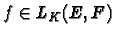 et
et
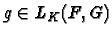 alors
alors
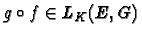 .
.
Définition 26
Si
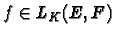
,
on définit :
- 1.
-
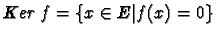 ,
le noyau de f.
,
le noyau de f.
- 2.
-
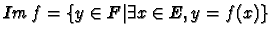 l'image de f.
l'image de f.
Proposition 11
- 1.
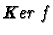 est un sous espace vectoriel de E.
est un sous espace vectoriel de E.
- 2.
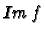 est un sous espace vectoriel de F.
est un sous espace vectoriel de F.
- 3.
- f est injective si et seulement si
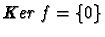 .
.
Preuve : en exercice.
Théorème 29 (admis)
Soient
E et
F deux K-e.v. de dimensions finies,
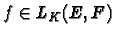
alors :
Définition 27
La dimension de l'image de
f est appelée le rang de
f et est notée
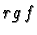
.
Proposition 12
Si
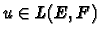
,
on a :
u est surjective si et seulement si
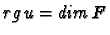
.
On admettra enfin la propriété importante suivante :
Proposition 13
Si
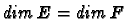
,
on a les équivalences suivantes :
- i)
- u est injective.
- ii)
- u est surjective.
- iii)
- u est un isomorphisme.
- iv)
- L'image par u d'une base de E est une base de F.
Proposition 14
Soit
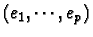
la base canonique de
Rp et
f une application linéaire de
Rp
dans
Rn.
L'application linéaire
f est déterminée par les images
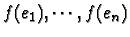
des vecteurs
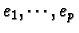
.
Preuve :
Si
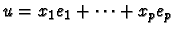 alors
alors
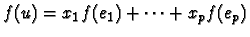 .
Si donc on connaît
l'image des vecteurs de base par f, on connaît l'image de tous les vecteurs, donc f est
entièrement déterminée.
.
Si donc on connaît
l'image des vecteurs de base par f, on connaît l'image de tous les vecteurs, donc f est
entièrement déterminée.
Exemple :
On note (e1,e2) et (l1,l2,l3) les bases canoniques respectives de R2 et R3.
Si
f(e1)=2l1+l2-l3 et
f(e2)=-l1+3l2+l3, alors l'image du vecteur
u=x1 e1 +x2e2
par f est
Définition 28
Soit
f une application linéaire de
Rp dans
Rn ; on note
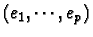
et
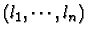
les bases canoniques respectives de
Rp et
Rn.
La matrice
M associée à
f relativement aux bases canoniques de
Rp et
Rn est le
tableau dont les colonnes sont les coordonnées des vecteurs
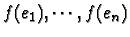
dans la
base canonique
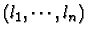
de
Rn.
Notation
On note habituellement aij le coefficient de la matrice M situé à l'intersection de la i-ème
ligne et de la j-ème colonne.
Ainsi pour tout entier j tel que
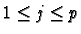 :
:
et
Remarque 15
- 1.
- M est une matrice rectangulaire (n,p) où n est le nombre de lignes et p le nombre
de colonnes. Une écriture symbolique de la matrice M est
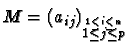 .
.
- 2.
- Si n=p la matrice est carrée.
- 3.
- Si n=1 alors M est une matrice ligne.
- 4.
- Si p=1 alors M est une matrice colonne.
Deux matrices sont égales si et seulement si elles ont même taille et si leurs coefficients de
mêmes indices sont égaux deux à deux.
Définition 29
Soit
A=(
aij) et
B=(
bij) deux matrices de même taille. La matrice somme de
A et
B est
la matrice
C=(
cij) de même taille telle que :
Proposition 15
On démontre que l'ensemble des matrices de taille (n,p) muni de l'addition est un groupe
commutatif.
L'élément neutre est la matrice dont tous les coefficients sont nuls.
Définition 30
Soit
A=(
aij) une matrice et
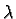
un réel. La matrice produit de
A par
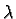
est
la matrice
D=(
dij) de même taille que
A telle que :
Proposition 16
On démontre que l'ensemble des matrices de taille (n,p) muni de l'addition et de la multiplication
par un réel est un R-espace vectoriel.
Définition 31
Soit
A=(
aij) une matrice (
n,
p) et
B=(
bij) une matrice (
p,
q). La matrice produit de
A
et
B est la matrice
AB=(
cij) de taille (
n,
q) définie par :
Remarque 16
- 1.
- On ne peut définir le produit AB de deux matrices A et B que si le nombre de
colonnes de A est égal au nombre de lignes de B.
- 2.
- Le produit de matrices n'est donc pas commutatif.
Pour voir cela on peut aussi considérer les matrices
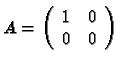 et
et
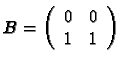 .
.
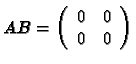 et
et
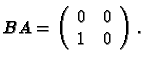
De plus on constate sur cet exemple que si 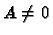 et
et 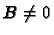 on peut tout de même avoir
AB=0.
on peut tout de même avoir
AB=0.
- 3.
- La multiplication s'effectue ligne par colonne : le premier coefficient de la matrice produit
s'obtient en faisant le "produit" de la première ligne et de la première colonne.
Proposition 17
On démontre que pour des matrices
A,
B et
C quelconques, sous réserve que les
produits considérés existent et pour tout réel
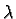
on a :
L'élément neutre est la matrice dont tous les coefficients sont nuls.
Dans le cas des matrices carrées d'ordre
n, la matrice notée
I et définie par :
aii=1 pour
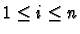
et
aij =0 pour
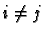
vérifie :
A x
I =
I x
A =
A pour
toute matrice carrée
A d'ordre
n. On l'appelle matrice unité ou identité.
Remarque 17
Les propriétés du calcul matriciel permettent d'obtenir des résultats sur une matrice
A
sans avoir à effectuer des calculs sur ses nombreux coefficients.
Par exemple, si une matrice carrée
A vérifie
A2 = -4
A +2
I, alors il existe une matrice
A'
telle que
A x
A' =
A' x
A =
I. En effet on a les égalités suivantes :
donc il suffit de prendre
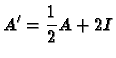
.
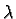 du corps K et le vecteur u de E,
du corps K et le vecteur u de E,
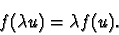
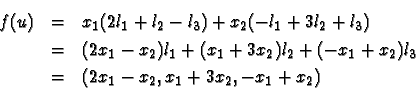

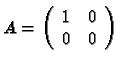 et
et
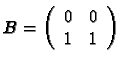 .
.
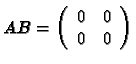 et
et
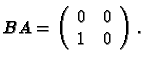
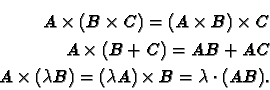
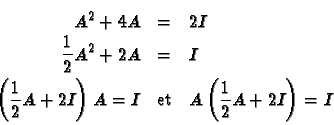
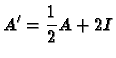 .
.