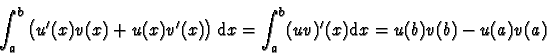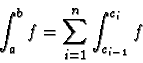
 est linéaire de CM dans R.
est linéaire de CM dans R.
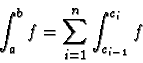
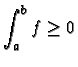 .
.
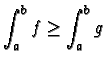 .
.
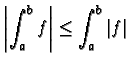 .
.
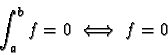
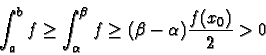
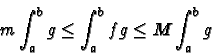
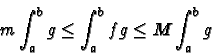
![\begin{displaymath}\exists c \in [a,b], \quad \int_{a}^{b} fg = f(c) \int_{a}^{b} g \end{displaymath}](makuhtmlimg87.gif)
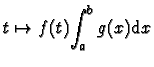 est continue comme f. Elle prend donc
toutes les valeurs comprises entre ses bornes qui sont
est continue comme f. Elle prend donc
toutes les valeurs comprises entre ses bornes qui sont
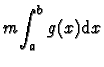 et
et
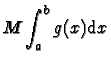 (théorème des valeurs intermédiaires).
D'après ce qui précède, il existe donc c dans [a,b] tel que
(théorème des valeurs intermédiaires).
D'après ce qui précède, il existe donc c dans [a,b] tel que
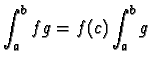 .
.
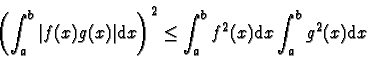
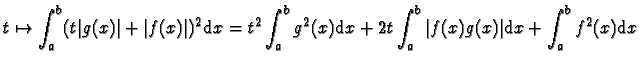 qui est :
qui est :
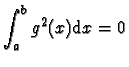 une fonction affine toujours
positive donc nécessairement constante, ce qui implique
une fonction affine toujours
positive donc nécessairement constante, ce qui implique
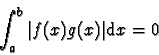
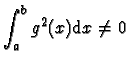 une fonction trinôme du second
degré toujours
positive ou nulle donc de discriminant négatif ou nul, ce qui s'écrit :
une fonction trinôme du second
degré toujours
positive ou nulle donc de discriminant négatif ou nul, ce qui s'écrit :
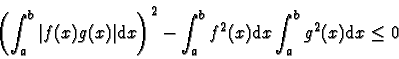
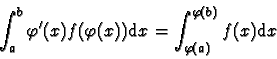
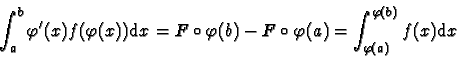
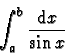
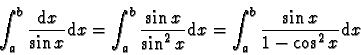
![\begin{displaymath}\int_{\cos a}^{\cos b} \frac{\mathrm{d}x}{x^2 -1}
= \int_{\c...
... \vert x-1\vert - \ln \vert x+1\vert \right]_{\cos a}^{\cos b}
\end{displaymath}](makuhtmlimg111.gif)
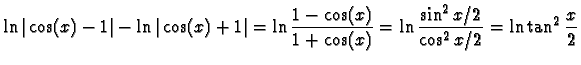 et donc finalement :
et donc finalement :

![\begin{displaymath}
\int_{a}^{b} u'(x)v(x) \mathrm{d}x = u(b)v(b)-u(a)v(a) -\int...
...[ u(x)v(x) \right]_{a}^{b} -\int_{a}^{b} u(x)v'(x) \mathrm{d}x
\end{displaymath}](makuhtmlimg114.gif)