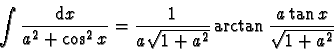Soit I un intervalle de R d'intérieur non vide. Soit
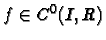 .
Alors
f admet des primitives qui sont les fonctions de la forme
.
Alors
f admet des primitives qui sont les fonctions de la forme
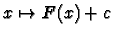 où F est l'une
d'entre elles que nous conviendrons de noter
où F est l'une
d'entre elles que nous conviendrons de noter
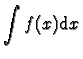 .
.
Exemples :
- 1.
-
sur les intervalles où  ne s'annule pas
(on s'est ramené ici à la primitive connue
ne s'annule pas
(on s'est ramené ici à la primitive connue
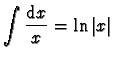 ).
).
- 2.
-
(on s'est ramené à la primitive
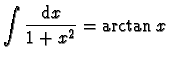 ).
).
Cette technique est à envisager dès qu'on est en présence de fonctions transcendantes
(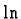 ,
,
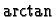 ,
,
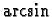 ,
...) ayant une dérivée de type algébrique.
,
...) ayant une dérivée de type algébrique.
Exemple
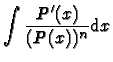 ,
,
![$n \in \mathbb{N},
P \in P[X]$](makuhtmlimg130.gif)
(Rappel P[X] désigne l'ensemble des polynômes à une indeterminée sur R. De même,
on notera P(X), celui des fractions rationnelles à une indeterminée sur R)
- 1.
- si n=1,
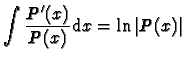 sur tout intervalle sur lequel P
ne s'annule pas.
sur tout intervalle sur lequel P
ne s'annule pas.
- 2.
- si n>1,
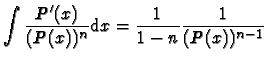 sur tout
intervalle sur lequel P ne s'annule pas.
sur tout
intervalle sur lequel P ne s'annule pas.
- i)
- On décompose en éléments simples de R(X).
- ii)
- On cherche une primitive de chaque terme.
- la partie entière est un polynôme
- les éléments simples de première espèce :
Exemple :
sur l'un des intervalles ![$]-\infty,0[$](makuhtmlimg136.gif) ,
]0,1[ ou
,
]0,1[ ou ![$]1,+ \infty [$](makuhtmlimg137.gif) .
.
- les éléments simples de seconde espèce :
Le premier terme s'intègre immédiatement.
Le second se ramène à
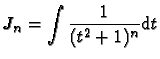 ,
,
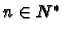 en mettant
le trinôme sous forme canonique et en effectuant le changement de variable approprié.
(Rappel :
en mettant
le trinôme sous forme canonique et en effectuant le changement de variable approprié.
(Rappel :
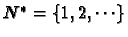 )
)
: on se propose de donner ici deux méthodes de calcul de l'intégrale Jn
définie ci-dessus.
- 1)
- Calculer Jn par récurrence :
- i)
- Calculer J1.
- ii)
- Exprimer Jn en fonction de Jn+1.
- iii)
- En utilisant une intégration par parties, montrer que :
et en déduire une relation de récurrence entre Jn+1 et Jn.
- 2)
- Calculer Jn par changement de variable :
Poser 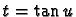 pour montrer que le calcul de Jn se ramène au calcul de
pour montrer que le calcul de Jn se ramène au calcul de
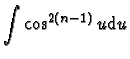 .
Il reste donc à linéariser cette dernière intégrale.
.
Il reste donc à linéariser cette dernière intégrale.
Exemple :
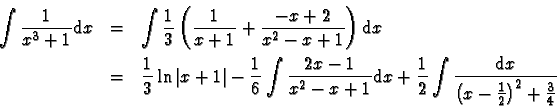
Posons
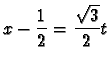 ,
il vient alors :
,
il vient alors :
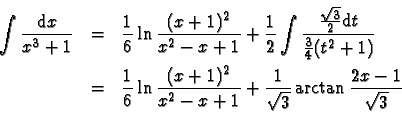
- 1)
-
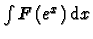 ,
,
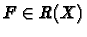 .
.
Le changement de variable ex = t nous ramène directement à la recherche d'une primitive de
fraction rationnelle en t :
- 2)
-
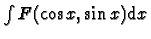 ,
,
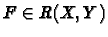 .
.
- i)
- Cas particulier du polynôme en
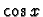 et
et 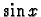 .
.
La linéarité de l'intégrale nous ramène au calcul des intégrales de type
 si m est pair, on pose
si m est pair, on pose 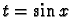 .
.
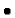 si n est impair, on pose
si n est impair, on pose 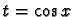 .
.
On est alors ramené à un polynôme en t.
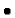 si M et n sont pairs, on peut linéariser le produit au moyen des exponentielles
complexes.
si M et n sont pairs, on peut linéariser le produit au moyen des exponentielles
complexes.
On peut aussi essayer d'obtenir (comme pour les intégrales de Wallis par exemple) des
relations de récurrence.
- ii)
- Cas général :
On dispose d'une règle générale :
- i)
- Cas particulier du polynôme en
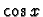 et
et 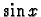 .
.
La linéarité de l'intégrale nous ramène au calcul des intégrales de type
 si m est pair, on pose
si m est pair, on pose 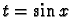 .
.
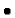 si n est impair, on pose
si n est impair, on pose 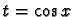 .
.
On est alors ramené à un polynôme en t.
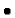 si M et n sont pairs, on peut linéariser le produit au moyen des exponentielles
complexes.
si M et n sont pairs, on peut linéariser le produit au moyen des exponentielles
complexes.
On peut aussi essayer d'obtenir (comme pour les intégrales de Wallis par exemple) des
relations de récurrence.
- ii)
- Cas général :
On dispose d'une règle générale :
[1)]
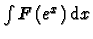 ,
,
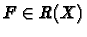 .
.
Le changement de variable ex = t nous ramène directement à la recherche d'une primitive de
fraction rationnelle en t :
[2)]
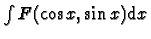 ,
,
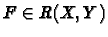 .
.
- i)
- Cas particulier du polynôme en
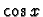 et
et 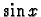 .
.
La linéarité de l'intégrale nous ramène au calcul des intégrales de type
 si m est pair, on pose
si m est pair, on pose 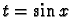 .
.
 si n est impair, on pose
si n est impair, on pose 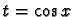 .
.
On est alors ramené à un polynôme en t.
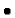 si M et n sont pairs, on peut linéariser le produit au moyen des exponentielles
complexes.
si M et n sont pairs, on peut linéariser le produit au moyen des exponentielles
complexes.
On peut aussi essayer d'obtenir (comme pour les intégrales de Wallis par exemple) des
relations de récurrence.
- ii)
- Cas général :
On dispose d'une règle générale :
[i)] Cas particulier du polynôme en 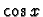 et
et 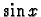 .
.
La linéarité de l'intégrale nous ramène au calcul des intégrales de type
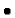 si m est pair, on pose
si m est pair, on pose 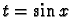 .
.
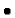 si n est impair, on pose
si n est impair, on pose 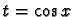 .
.
On est alors ramené à un polynôme en t.
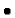 si M et n sont pairs, on peut linéariser le produit au moyen des exponentielles
complexes.
si M et n sont pairs, on peut linéariser le produit au moyen des exponentielles
complexes.
On peut aussi essayer d'obtenir (comme pour les intégrales de Wallis par exemple) des
relations de récurrence.
[ii)] Cas général :
On dispose d'une règle générale :
Si la forme différentielle
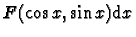 est invariante par le changement :
est invariante par le changement :
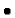 de x en -x, poser
de x en -x, poser 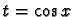
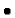 de x en
de x en 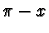 ,
poser
,
poser 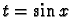
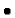 de x en
de x en 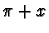 ,
poser
,
poser 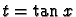
Sinon, poser
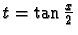
On se retrouve dans tous les cas avec le calcul d'une primitive d'une fraction rationnelle en t.
Exemple :
Si 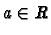 ,
on cherche
,
on cherche
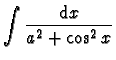 .
.
La forme différentielle étant invariante par le changement de x en 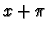 ,
on pose donc
,
on pose donc
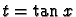 .
Il vient :
.
Il vient :
En posant maintenant
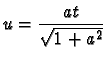 ,
il vient
,
il vient
et finalement
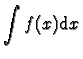 .
.
![]() .
Alors
f admet des primitives qui sont les fonctions de la forme
.
Alors
f admet des primitives qui sont les fonctions de la forme
![]() où F est l'une
d'entre elles que nous conviendrons de noter
où F est l'une
d'entre elles que nous conviendrons de noter
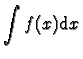 .
.
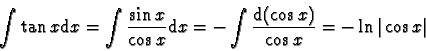
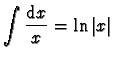 ).
).
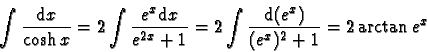
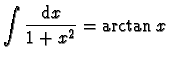 ).
).
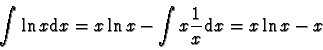
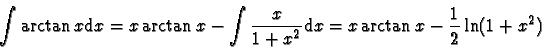
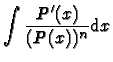 ,
,
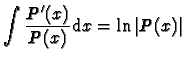 sur tout intervalle sur lequel P
ne s'annule pas.
sur tout intervalle sur lequel P
ne s'annule pas.
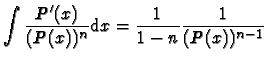 sur tout
intervalle sur lequel P ne s'annule pas.
sur tout
intervalle sur lequel P ne s'annule pas.
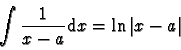
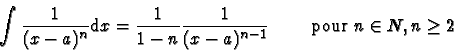
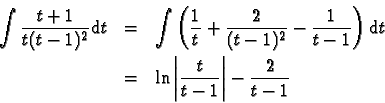
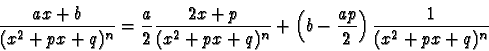
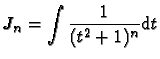 ,
,
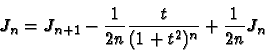
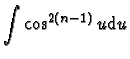 .
Il reste donc à linéariser cette dernière intégrale.
.
Il reste donc à linéariser cette dernière intégrale.
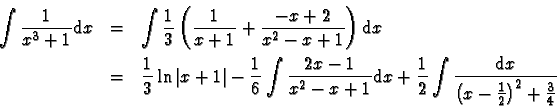
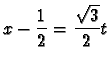 ,
il vient alors :
,
il vient alors :
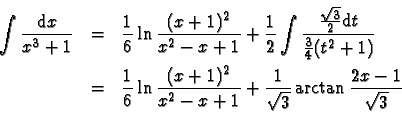
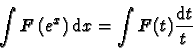
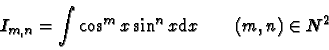
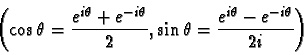
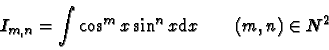
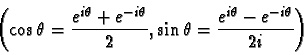
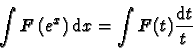
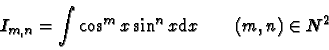
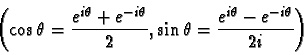
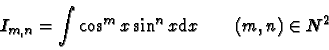
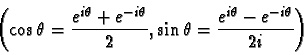
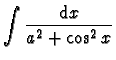 .
.
![\begin{eqnarray*}
\int \frac{\mathrm{d}x}{a^2 + \cos^2 x} &=& \int \frac{\mathrm...
... \left[ \left( \frac{a t}{ \sqrt{1+a^2} } \right)^2 +1 \right] }
\end{eqnarray*}](makuhtmlimg169.gif)
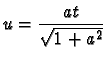 ,
il vient
,
il vient
![\begin{eqnarray*}
\int \frac{\mathrm{d}x}{a^2 + \cos^2 x} = \int \frac{ \frac{ \sqrt{1+a^2} }{a} \mathrm{d}u }{(1+a^2)[1+u^2]}
\end{eqnarray*}](makuhtmlimg171.gif)