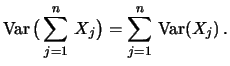Interessiert man sich gleichzeitig für mehrere
Zufallsgrößen
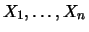
- z.B. die
Kurse verschiedener Aktien - und für ihre wechselseitige
Abhängigkeit, so betrachtet man
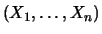 als
zufälligen Punkt oder Zufallsvektor im
als
zufälligen Punkt oder Zufallsvektor im
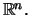 Die
gemeinsame Verteilung der
Zufallsgrößen
Die
gemeinsame Verteilung der
Zufallsgrößen
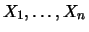 , d.h. die Verteilung des
Zufallsvektors, wird wie im eindimensionalen eindeutig durch die
Wahrscheinlichkeiten
, d.h. die Verteilung des
Zufallsvektors, wird wie im eindimensionalen eindeutig durch die
Wahrscheinlichkeiten
bestimmt. Besitzt der Zufallsvektor
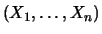 eine Wahrscheinlichkeitsdichte
eine Wahrscheinlichkeitsdichte
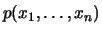 , so
können Wahrscheinlichkeiten wieder als Integrale von
, so
können Wahrscheinlichkeiten wieder als Integrale von 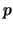 berechnet werden:
berechnet werden:
Die eindimensionalen Verteilungen oder
Randverteilungen von 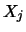
erhält man durch Integration der gemeinsame
Dichte über die anderen Variablen.
Der intuitive Begriff der Unabhängigkeit zweier
Zufallsgrößen 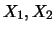 wird präzisiert durch die
Forderung, dass
wird präzisiert durch die
Forderung, dass
d.h. Wahrscheinlichkeiten von
Ereignissen, die von dem Wert des Zufallsvektors
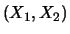 abhängen, lassen sich faktorisieren, und es genügt, die
eindimensionalen Verteilungen von
abhängen, lassen sich faktorisieren, und es genügt, die
eindimensionalen Verteilungen von 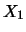 und
und 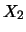 zu kennen.
Besitzt der Zufallsvektor
zu kennen.
Besitzt der Zufallsvektor
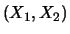 eine Dichte
eine Dichte
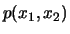 , so besitzen
, so besitzen 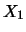 und
und 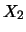 ebenfalls Dichten
ebenfalls Dichten 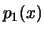 und
und
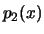 . Die Unabhängigkeit der beiden Zufallsgrößen ist
dann gleichbedeutend mit der Faktorisierung der gemeinsamen
Dichte:
Abhängigkeit zweier Zufallsgrößen
. Die Unabhängigkeit der beiden Zufallsgrößen ist
dann gleichbedeutend mit der Faktorisierung der gemeinsamen
Dichte:
Abhängigkeit zweier Zufallsgrößen 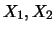 kann in komplizierter Form
vorliegen. Sind
kann in komplizierter Form
vorliegen. Sind 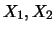 gemeinsam normalverteilt, lässt sich der Grad
ihrer Abhängigkeit aber auf einfache Weise quantifizieren durch ihre Kovarianz
oder Korrelation
Die Korrelation hat den Vorteil, immer zwischen - 1 und + 1 zu
liegen und skaleninvariant zu sein. Für gemeinsam normalverteilte Zufallsgrößen ist Unabhängigkeit
gleichbedeutend mit Korrelation gleich Null, während
vollständige Abhängigkeit gleichbedeutend mit Korrelation + 1
(
gemeinsam normalverteilt, lässt sich der Grad
ihrer Abhängigkeit aber auf einfache Weise quantifizieren durch ihre Kovarianz
oder Korrelation
Die Korrelation hat den Vorteil, immer zwischen - 1 und + 1 zu
liegen und skaleninvariant zu sein. Für gemeinsam normalverteilte Zufallsgrößen ist Unabhängigkeit
gleichbedeutend mit Korrelation gleich Null, während
vollständige Abhängigkeit gleichbedeutend mit Korrelation + 1
(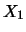 ist groß, wenn
ist groß, wenn 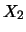 groß ist) oder Korrelation -1
groß ist) oder Korrelation -1
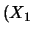 ist groß, wenn
ist groß, wenn 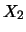 klein ist) ist.
klein ist) ist.
Allgemein gilt für unabhängige Zufallsgrößen
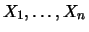
woraus eine nützliche Rechenregel folgt:
Sind
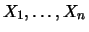 unabhängige Zufallsgrößen, die alle dieselbe
Verteilung haben:
unabhängige Zufallsgrößen, die alle dieselbe
Verteilung haben:
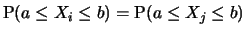
für alle
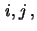
so nennen wir sie unabhängig identisch verteilt
(u.i.v.).
![]()
![]() als
zufälligen Punkt oder Zufallsvektor im
als
zufälligen Punkt oder Zufallsvektor im
![]() Die
gemeinsame Verteilung der
Zufallsgrößen
Die
gemeinsame Verteilung der
Zufallsgrößen
![]() , d.h. die Verteilung des
Zufallsvektors, wird wie im eindimensionalen eindeutig durch die
Wahrscheinlichkeiten
, d.h. die Verteilung des
Zufallsvektors, wird wie im eindimensionalen eindeutig durch die
Wahrscheinlichkeiten
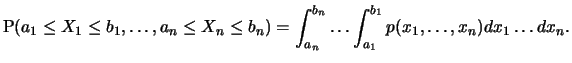
![]()
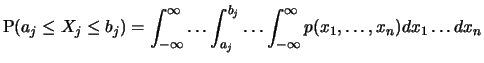
![]() wird präzisiert durch die
Forderung, dass
wird präzisiert durch die
Forderung, dass
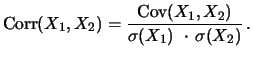
![]()