As indicated in the overview in Chapter 5, a partial linear model (PLM) consists of two additive
components, a linear and a nonparametric part:
where
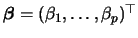 is a finite
dimensional parameter and
is a finite
dimensional parameter and
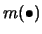 a smooth function. Here, we assume again a decomposition
of the explanatory variables into two vectors,
a smooth function. Here, we assume again a decomposition
of the explanatory variables into two vectors,
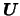 and
and
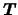 .
The vector
.
The vector
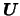 denotes a
denotes a 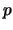 -variate random vector which typically covers categorical
explanatory variables or variables that are known to influence the index
in a linear way. The vector
-variate random vector which typically covers categorical
explanatory variables or variables that are known to influence the index
in a linear way. The vector
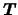 is a
is a 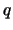 -variate random vector of
continuous explanatory variables which is to be modeled in a nonparametric
way. Economic theory or intuition should guide you as to which
regressors should be included in
-variate random vector of
continuous explanatory variables which is to be modeled in a nonparametric
way. Economic theory or intuition should guide you as to which
regressors should be included in
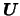 or
or
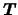 , respectively.
, respectively.
Obviously, there is a straightforward
generalization of this model to the case with a known link
function
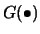 . We denote this semiparametric extension
of the GLM
. We denote this semiparametric extension
of the GLM
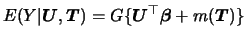 |
(7.1) |
as generalized partial linear model (GPLM).
![]() . We denote this semiparametric extension
of the GLM
. We denote this semiparametric extension
of the GLM