Thanks to Newton's laws, dropping a stone from a latitude of 10 m,
the point of time of its impact on the ground is known before
executing the experiment. Quantities in complex systems (such as
stock prices at a certain date, daily maximum temperature at a
certain place) are however not deterministically predictable,
although it is known which values are more likely to occur than
others. Contrary to the falling stone, data which cannot be
described successfully by deterministic mechanism, can be modelled
by random variables.
Let 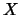 be such a random variable which, (as a model for stock
prices), takes values on the real time. The appraisal of which
values of
be such a random variable which, (as a model for stock
prices), takes values on the real time. The appraisal of which
values of 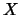 are more and which are less likely, is expressed by
the probability of events as
are more and which are less likely, is expressed by
the probability of events as
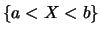 or
or
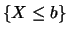 . The set of all probabilities
. The set of all probabilities
determines the distribution of 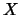 . In
other words, the distribution is defined by the probabilities of
all events which depend on
. In
other words, the distribution is defined by the probabilities of
all events which depend on 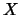 . In the following, we denote the
probability distribution of
. In the following, we denote the
probability distribution of 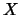 by
by
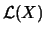 .
.
The probability distribution is uniquely defined by the cumulative probability distribution
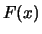 is monotonously increasing and converges for
is monotonously increasing and converges for
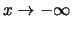 to 0, and for
to 0, and for
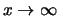 to
to 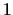 . If there
is a function
. If there
is a function 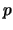 , such that the probabilities can be computed by
means of an integral
, such that the probabilities can be computed by
means of an integral
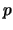 is called a probability density, or briefly
density of
is called a probability density, or briefly
density of 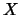 . Then the cumulative distribution function is a
primitive of
. Then the cumulative distribution function is a
primitive of 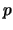 :
For small
:
For small 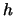 it holds:
Thus
it holds:
Thus 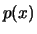 is a measure of the likelihood that
is a measure of the likelihood that 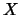 takes values
close to
takes values
close to 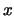 .
.
The most important family of distributions with densities, is the
normal distribution family. It is
characterized by two parameters
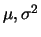 . The densities
are given by
. The densities
are given by
The distribution with density
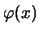 is called standard normal distribution. ``
is called standard normal distribution. ``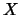 is a normal random variable with parameters
is a normal random variable with parameters
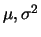 '' is commonly abbreviated by ``
'' is commonly abbreviated by ``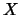 is
is
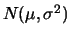 distributed''. The cumulative distribution function of
a standard normal distribution is denoted by
distributed''. The cumulative distribution function of
a standard normal distribution is denoted by 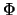 and it holds:
If
and it holds:
If 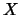 is
is
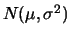 distributed, then the centered and
scaled random variable
distributed, then the centered and
scaled random variable
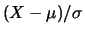 is standard normal
distributed. Therefore, its cumulative distribution function is
given by:
is standard normal
distributed. Therefore, its cumulative distribution function is
given by:
A distribution which is of importance in modelling stock prices is
the lognormal distribution.
Let 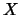 be a positive random variable whose natural logarithm
be a positive random variable whose natural logarithm
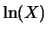 is normally distributed with parameters
is normally distributed with parameters
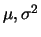 . We say that
. We say that 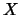 is lognormally distributed with parameters
is lognormally distributed with parameters
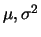 . Its cumulative distribution function follows
directly from the above definition:
. Its cumulative distribution function follows
directly from the above definition:
Deriving 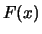 once, we obtain its density function with
parameters
once, we obtain its density function with
parameters
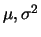 :
:
If 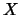 is a random variable that takes only finitely or countably
infinite values
is a random variable that takes only finitely or countably
infinite values
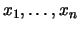 ,
, 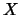 is said to be a discrete
random variable and its distribution is fully determined by the
probabilities:
is said to be a discrete
random variable and its distribution is fully determined by the
probabilities:
The simplest discrete random variables take only 2 or 3 values,
for example 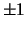 or
or
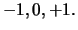 They constitute the
basis of binomial or trinomial trees which can be used to
construct discrete random processes in computers. Such tree
methods are reasonable approximations to continuous processes
which are used to model stock prices.
They constitute the
basis of binomial or trinomial trees which can be used to
construct discrete random processes in computers. Such tree
methods are reasonable approximations to continuous processes
which are used to model stock prices.
In this context, binomially distributed random variables appear. Let
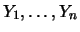 be independent random variables taking two
values, 0 or 1, with probabilities
be independent random variables taking two
values, 0 or 1, with probabilities
We call such random variables Bernoulli
distributed with
parameter 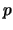 . The number of ones appearing in the sample
. The number of ones appearing in the sample
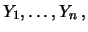 equals the sum
equals the sum
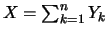 which is
binomial distributed with parameters
which is
binomial distributed with parameters 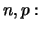
 SFEBinomial.xpl
SFEBinomial.xpl
Instead of saying 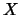 is binomial distributed with parameters
is binomial distributed with parameters 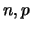 , we use the notation ``
, we use the notation ``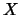 is
is 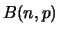 distributed''. Hence, a
Bernoulli distributed random variable is
distributed''. Hence, a
Bernoulli distributed random variable is 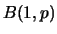 distributed.
distributed.
If 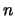 is large enough, a
is large enough, a 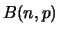 distributed random variable can
be approximated by a
distributed random variable can
be approximated by a
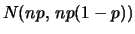 distributed random
variable
distributed random
variable 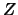 , in the sense that
, in the sense that
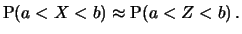 |
(4.1) |
The central limit theorem is more precise on that matter. In
classical statistics it is used to avoid, for large 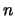 , the
tedious calculation of binomial probabilities. Conversely, it is
possible to approximate the normal distribution by an easy
simulated binomial tree.
, the
tedious calculation of binomial probabilities. Conversely, it is
possible to approximate the normal distribution by an easy
simulated binomial tree.
 SFEclt.xpl
SFEclt.xpl
![]() be such a random variable which, (as a model for stock
prices), takes values on the real time. The appraisal of which
values of
be such a random variable which, (as a model for stock
prices), takes values on the real time. The appraisal of which
values of ![]() are more and which are less likely, is expressed by
the probability of events as
are more and which are less likely, is expressed by
the probability of events as
![]() or
or
![]() . The set of all probabilities
. The set of all probabilities
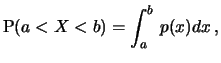
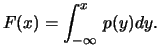
![]() . The densities
are given by
. The densities
are given by
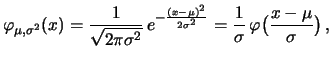
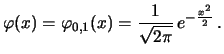
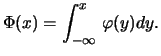
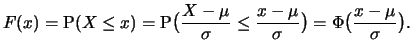
![]() be a positive random variable whose natural logarithm
be a positive random variable whose natural logarithm
![]() is normally distributed with parameters
is normally distributed with parameters
![]() . We say that
. We say that ![]() is lognormally distributed with parameters
is lognormally distributed with parameters
![]() . Its cumulative distribution function follows
directly from the above definition:
. Its cumulative distribution function follows
directly from the above definition:
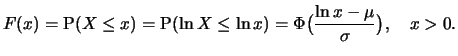
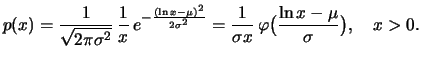
![]() is a random variable that takes only finitely or countably
infinite values
is a random variable that takes only finitely or countably
infinite values
![]() ,
, ![]() is said to be a discrete
random variable and its distribution is fully determined by the
probabilities:
is said to be a discrete
random variable and its distribution is fully determined by the
probabilities:
![]() be independent random variables taking two
values, 0 or 1, with probabilities
be independent random variables taking two
values, 0 or 1, with probabilities
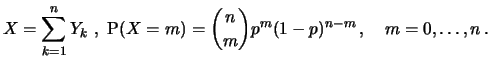
![]() is binomial distributed with parameters
is binomial distributed with parameters ![]() , we use the notation ``
, we use the notation ``![]() is
is ![]() distributed''. Hence, a
Bernoulli distributed random variable is
distributed''. Hence, a
Bernoulli distributed random variable is ![]() distributed.
distributed.
![]() is large enough, a
is large enough, a ![]() distributed random variable can
be approximated by a
distributed random variable can
be approximated by a
![]() distributed random
variable
distributed random
variable ![]() , in the sense that
, in the sense that