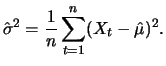The mathematical expectation or the mean
![$ \mathop{\text{\rm\sf E}}[X]$](sfehtmlimg47.gif) of a
real random variable
of a
real random variable 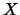 is a measure for the location of the
distribution of
is a measure for the location of the
distribution of 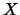 . Adding to
. Adding to 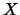 a real constant
a real constant 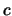 , it holds
for the expectation:
, it holds
for the expectation:
![$ \mathop{\text{\rm\sf E}}[X+c] = \mathop{\text{\rm\sf E}}[X] + c$](sfehtmlimg403.gif) , i.e. the location
of the distribution is translated. If
, i.e. the location
of the distribution is translated. If 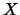 has a density
has a density 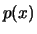 ,
its expectation is defined as:
If the integral does not exist, neither does the expectation. In
practice, this is rather rarely the case.
,
its expectation is defined as:
If the integral does not exist, neither does the expectation. In
practice, this is rather rarely the case.
Let
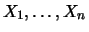 be a sample of identically independently
distributed (i.i.d.) random variables (see Section 3.4)
having the same distribution as
be a sample of identically independently
distributed (i.i.d.) random variables (see Section 3.4)
having the same distribution as 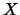 , then
, then
![$ \mathop{\text{\rm\sf E}}[X]$](sfehtmlimg47.gif) can be estimated
by means of the sample mean:
can be estimated
by means of the sample mean:
A measure for the dispersion of a random variable 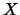 around its
mean is given by the variance
around its
mean is given by the variance
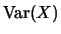 :
:
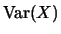 |
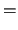 |
![$\displaystyle \mathop{\text{\rm\sf E}}[(X - \mathop{\text{\rm\sf E}}X)^2]$](sfehtmlimg410.gif) |
|
| Variance |
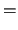 |
mean squarred deviation of a random variable |
|
| |
 |
around its expectation. |
|
If 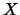 has a density
has a density 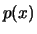 , its variance can be computed as
follows:
The integral can be infinite. There are empirical studies giving
rise to doubt that some random variables appearing in financial
and actuarial mathematics and which model losses in highly risky
businesses dispose of a finite variance.
, its variance can be computed as
follows:
The integral can be infinite. There are empirical studies giving
rise to doubt that some random variables appearing in financial
and actuarial mathematics and which model losses in highly risky
businesses dispose of a finite variance.
As a quadratic quantity the variance's unity is different from
that of 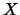 itself. It is better to use the standard deviation of
itself. It is better to use the standard deviation of
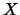 which is measured in the same unity as
which is measured in the same unity as 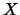 :
:
Given a sample of i.i.d. variables
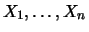 which have the
same distribution as
which have the
same distribution as 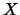 , the sample variance can be estimated
by:
, the sample variance can be estimated
by:
A
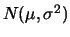 distributed random variable
distributed random variable 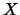 has mean
has mean
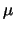 and variance
and variance 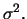 The
The 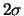 area around
area around 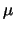 contains with probability of a little more than 95% observations
of
contains with probability of a little more than 95% observations
of 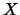 :
A lognormally distributed random variable
:
A lognormally distributed random variable 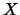 with parameters
with parameters
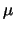 and
and 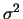 has mean and variance
A
has mean and variance
A 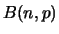 distributed variable
distributed variable 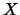 has mean
has mean 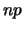 and variance
and variance
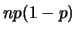 . The approximation (3.1) is chosen such that the
binomial and normal distribution have identical mean and variance.
. The approximation (3.1) is chosen such that the
binomial and normal distribution have identical mean and variance.
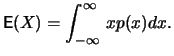
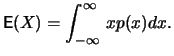
![]() be a sample of identically independently
distributed (i.i.d.) random variables (see Section 3.4)
having the same distribution as
be a sample of identically independently
distributed (i.i.d.) random variables (see Section 3.4)
having the same distribution as ![]() , then
, then
![]() can be estimated
by means of the sample mean:
can be estimated
by means of the sample mean:
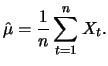
![]() around its
mean is given by the variance
around its
mean is given by the variance
![]() :
:
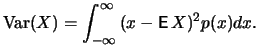
![]() itself. It is better to use the standard deviation of
itself. It is better to use the standard deviation of
![]() which is measured in the same unity as
which is measured in the same unity as ![]() :
:
![]() which have the
same distribution as
which have the
same distribution as ![]() , the sample variance can be estimated
by:
, the sample variance can be estimated
by: