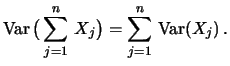A
random vector (
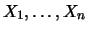 ) from
) from
 can be
useful in describing the mutual dependencies of several random
variables
can be
useful in describing the mutual dependencies of several random
variables
 , for example several underlying
stocks. The joint distribution of the random variables
, for example several underlying
stocks. The joint distribution of the random variables
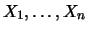 is as in the univariate case, uniquely determined by
the probabilities
If the random vector (
is as in the univariate case, uniquely determined by
the probabilities
If the random vector (
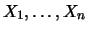 ) has a density
) has a density
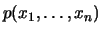 , the probabilities can be computed by means of the
following integrals:
, the probabilities can be computed by means of the
following integrals:
The univariate or marginal distribution of 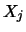 can be computed from the joint density by
integrating out the variable not of interest.
can be computed from the joint density by
integrating out the variable not of interest.
The intuitive notion of independence of two random variables
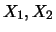 is formalized by requiring:
is formalized by requiring:
i.e. the joint probability of two
events depending on the random vector (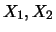 ) can be
factorized. It is sufficient to consider the univariate
distributions of
) can be
factorized. It is sufficient to consider the univariate
distributions of 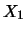 and
and 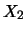 exclusively. If the random vector
(
exclusively. If the random vector
(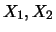 ) has a density
) has a density
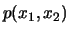 , then
, then 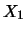 and
and 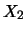 have densities
have densities 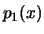 and
and 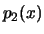 as well. In this case,
independence of both random variables is equivalent to a joint
density which can be factorized:
Dependence of two random variables
as well. In this case,
independence of both random variables is equivalent to a joint
density which can be factorized:
Dependence of two random variables 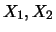 can be very
complicated. If
can be very
complicated. If 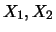 are jointly normally distributed, their
dependency structure can be rather easily quantified by their
covariance:
as well as by their correlation:
The correlation has the advantage of taking values between -1 and
+1, which is scale invariant. For jointly normally distributed
random variables, independence is equivalent to zero correlation,
while complete dependence is equivalent to either a correlation of
+1 (
are jointly normally distributed, their
dependency structure can be rather easily quantified by their
covariance:
as well as by their correlation:
The correlation has the advantage of taking values between -1 and
+1, which is scale invariant. For jointly normally distributed
random variables, independence is equivalent to zero correlation,
while complete dependence is equivalent to either a correlation of
+1 (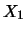 is large when
is large when 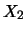 is large) or a correlation of -1
(
is large) or a correlation of -1
(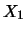 is large when
is large when 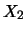 is small).
is small).
In general, it holds for independent random variables
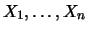
This implies a useful computation rule:
If
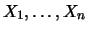 are independent and have all the same
distribution:
are independent and have all the same
distribution:
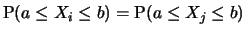
for all
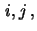
we call them independently and identically
distributed (i.i.d.).
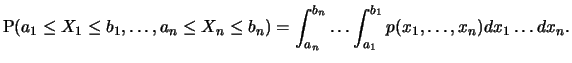
![]() can be computed from the joint density by
integrating out the variable not of interest.
can be computed from the joint density by
integrating out the variable not of interest.
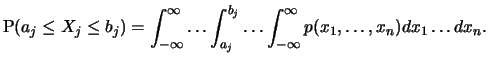
![]() is formalized by requiring:
is formalized by requiring:
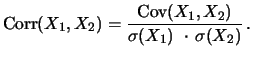
![]()