5.3 General Random Walks

Binomial and trinomial processes are simple examples for general random walks, i.e. stochastic processes $\{ X_t; \, t \ge 0 \}$ satisfying:

$$X_t = X_0 + \sum^t_{k=1} \, Z_k \, , \qquad t = 1, 2, \ldots$$

where $X_0$ is independent of $Z_1, Z_2, \ldots$ which are i.i.d. The increments have a distribution of a real valued random variable. $Z_k$ can take a finite or countably infinite number of values; but it is also possible for $Z_k$ to take values out of a continuous set.

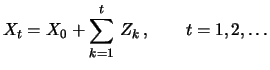
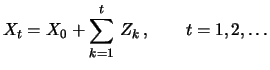
As an example, consider a Gaussian random walk with $X_0 = 0$, where the finitely many $X_1, \ldots, X_t$ are jointly normally distributed. Such a random walk can be constructed by assuming identically, independently and normally distributed increments. By the properties of the normal distribution, it follows that $X_t$ is $N (\mu t, \, \sigma^2 t)$-distributed for each $t$. If $X_0 = 0$ and $\mathop{\text{\rm Var}}(Z_1)$ is finite, it holds approximately for all random walks for $t$ large enough:

$$\mathcal{L} (X_t) \approx N (t \cdot \mathop{\text{\rm\sf E}}[Z_1], \ t \cdot \mathop{\text{\rm Var}}(Z_1)).$$

This result follows directly from the central limit theorem for i.i.d. random variables.

Random walks are processes with independent increments. That means, the increment $Z_{t+1}$ of the process from time $t$ to time $t+1$ is independent of the past values $X_0, \ldots, X_t$ up to time $t$. In general, it holds for any $s>0$ that the increment of the process from time $t$ to time $t+s$

$$X_{t+s} - X_t = Z_{t+1} + \ldots + Z_{t+s}$$

is independent of $X_0, \ldots, X_t.$ It follows that the best prediction, in terms of mean squared error, for $X_{t+1}$ given $X_0, \ldots, X_t$ is just $X_t + \mathop{\text{\rm\sf E}}[Z_{t+1}] \, .$ As long as the price of only one stock is considered, this prediction rule works quite well. Already hundred years ago, Bachelier postulated (assuming $\mathop{\text{\rm\sf E}}[Z_k] = 0$ for all $k$):``The best prediction for the stock price of tomorrow is the price of today.''

Processes with independent increments are also Markov-processes. In other words, the future evolution of the process in time $t$ depends exclusively on $X_t$, and the value of $X_t$ is independent of the past values $X_0, \ldots, X_{t-1}.$ If the increments $Z_k$ and the starting value $X_0$, and hence all $X_t$, can take a finite or countably infinite number of values, then the Markov-property is formally expressed by:

$$\P(a_{t+1} < X_{t+1} < b_{t+1} \vert X_t = c, \, a_{t-1} < X_{t-1} < b_{t-1}, \ldots, \, a_0 < X_0 < b_0 )$$

$$= \P(a_{t+1} < X_{t+1} < b_{t+1} \vert X_t = c) \, .$$

If $X_t = c$ is known, additional information about $X_0, \ldots, X_{t-1}$ does not influence the opinion about the range in which $X_t$ will probably fall.