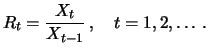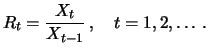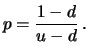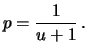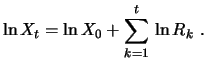The essential idea underlying the random walk for real processes
is the assumption of mutually independent increments of the order
of magnitude for each point of time. However, economic time series
in particular do not satisfy the latter assumption. Seasonal
fluctuations of monthly sales figures for example are in absolute terms significantly greater if the yearly average sales
figure is high. By contrast, the relative or percentage changes
are stable over time and do not depend on the current level of
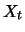 . Analogously to the random walk with i.i.d. absolute
increments
. Analogously to the random walk with i.i.d. absolute
increments
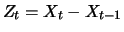 , a geometric random
walk
, a geometric random
walk
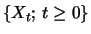 is assumed to have i.i.d. relative increments
For example, a geometric binomial random walk is given by
is assumed to have i.i.d. relative increments
For example, a geometric binomial random walk is given by
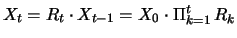 |
(5.5) |
where
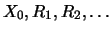 are mutually independent and for
are mutually independent and for
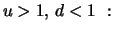 Given the independence assumption and
Given the independence assumption and
![$ \mathop{\text{\rm\sf E}}[R_k] = (u-d) p+d$](sfehtmlimg586.gif) it
follows from equation (4.5) that
it
follows from equation (4.5) that
![$ \mathop{\text{\rm\sf E}}[X_t]$](sfehtmlimg587.gif) increases or
decreases exponentially as the case may be
increases or
decreases exponentially as the case may be
![$ \mathop{\text{\rm\sf E}}[R_k] > 1$](sfehtmlimg588.gif) or
or
![$ \mathop{\text{\rm\sf E}}
[R_k] < 1$](sfehtmlimg589.gif) :
If
:
If
![$ \mathop{\text{\rm\sf E}}[R_k] = 1$](sfehtmlimg591.gif) the process is on average stable, which is the
case for
For a recombining process, i.e.
the process is on average stable, which is the
case for
For a recombining process, i.e.
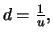 this
relationship simplifies to
Taking logarithms in equation (4.5) yields:
The process
this
relationship simplifies to
Taking logarithms in equation (4.5) yields:
The process
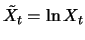 is itself an ordinary binomial
process with starting value
is itself an ordinary binomial
process with starting value 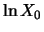 and increments
and increments
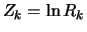 for which hold:
For
for which hold:
For  large,
large,
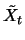 is approximately normally
distributed, i.e.
is approximately normally
distributed, i.e.
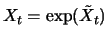 is approximately
lognormally distributed.
is approximately
lognormally distributed.