Binomial processes and more general random walks model the stock
price at best locally. They proceed from the assumption that the
distribution of the increments
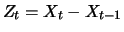 are the same
for each value
are the same
for each value 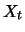 , regardless of whether the stock price is
substantially greater or smaller than
, regardless of whether the stock price is
substantially greater or smaller than 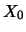 . Absolute increments
. Absolute increments
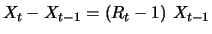 of a geometric random walk
depend on the level of
of a geometric random walk
depend on the level of 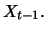 Thus, geometric random walks are
processes which do not have independent absolute increments.
Unfortunately, modelling the stock price dynamics globally the
latter processes are too simple to explain the impact of the
current price level on the future stock price evolution. A class
of processes which take this effect into account are binomial
processes with state dependent (and possibly time dependent)
increments:
Thus, geometric random walks are
processes which do not have independent absolute increments.
Unfortunately, modelling the stock price dynamics globally the
latter processes are too simple to explain the impact of the
current price level on the future stock price evolution. A class
of processes which take this effect into account are binomial
processes with state dependent (and possibly time dependent)
increments:
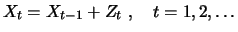 |
(5.6) |
Since the distribution of 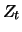 depends on
the state
depends on
the state 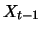 and possibly on time
and possibly on time  , increments are
neither independent nor identically distributed. The deterministic
functions
, increments are
neither independent nor identically distributed. The deterministic
functions 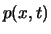 associate a probability to each possible value
of the process at time
associate a probability to each possible value
of the process at time  and to each
and to each  . Stochastic processes
. Stochastic processes
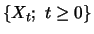 which are constructed as in
(4.6) are still markovian but without having
independent increments.
which are constructed as in
(4.6) are still markovian but without having
independent increments.
Accordingly, geometric binomial processes with state dependent
relative increments can be defined (for
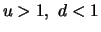 ):
):
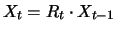 |
(5.7) |
Processes as defined in (4.6) and
(4.7) are mainly of theoretic interest, since without
further assumptions it is rather difficult to estimate the
probabilities 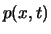 from observed stock prices. But
generalized binomial models (as well as the trinomial models) can
be used to solve differential equations numerically, as the
Black-Scholes equation for American options for example.
from observed stock prices. But
generalized binomial models (as well as the trinomial models) can
be used to solve differential equations numerically, as the
Black-Scholes equation for American options for example.
![]() ):
):