For a given
stochastic process one is often interested in the connection
between two random variables of a process at different points in
time. One way to measure a linear relationship is with the ACF,
i.e., the correlation between these two variables. Another way to
measure the connection between 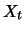 and
and
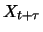 is to
filter out of
is to
filter out of 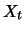 and
and
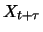 the linear influence of the
random variables that lie in between,
the linear influence of the
random variables that lie in between,
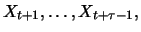 and then calculate the correlation
of the transformed random variables. This is called the partial autocorrelation.
and then calculate the correlation
of the transformed random variables. This is called the partial autocorrelation.
Definition 12.3 (Partial autocorrelation)
The partial autocorrelation of
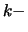
th order is defined as
where
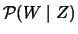
is the best linear projection of
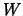
on
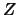
, i.e.,
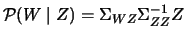
with
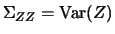
as the covariance matrix of the regressors
and

as the matrix of covariances between
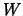
and
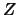
.
The `best linear projection' is understood in the sense of
minimizing the mean squared error.
An equivalent definition is the solution to the system of
equations
with
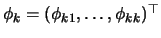 and
and
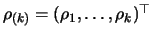 . These are the Yule-Walker
equations for an AR(
. These are the Yule-Walker
equations for an AR(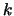 ) process. The last coefficient,
) process. The last coefficient,
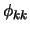 , is the partial autocorrelation of order
, is the partial autocorrelation of order 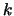 , as
defined above. Since only this coefficient is of interest in this
context, the system of equations can be solved for
, as
defined above. Since only this coefficient is of interest in this
context, the system of equations can be solved for 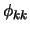 using the Cramer-Rule. We get
where
using the Cramer-Rule. We get
where 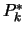 is equal to the matrix
is equal to the matrix 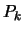 , in which the
, in which the 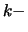 th
column is replaced with
th
column is replaced with
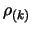 . Here
. Here 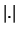 indicates the
determinant. Since this can be applied for various orders
indicates the
determinant. Since this can be applied for various orders 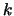 , in
the end we obtain a partial autocorrelation function (PACF).
The PACF can be graphically displayed for a given stochastic
process, similar to the ACF as a function of order
, in
the end we obtain a partial autocorrelation function (PACF).
The PACF can be graphically displayed for a given stochastic
process, similar to the ACF as a function of order 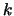 . This is
called the partial autocorrelogram.
. This is
called the partial autocorrelogram.
From the definition of PACF it immediately follows that there is
no difference between PACF and ACF of order 1:
For order 2 we have
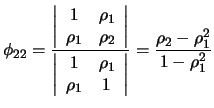 |
(12.18) |
Example 12.3 (AR(1))
The AR(1) process
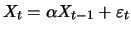
has the
ACF
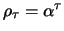
. For the PACF we have
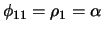
and
and
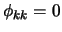
for all
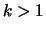
. This is plausible since the last
coefficient of an AR(
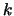
) model for this process is zero for all
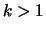
. For
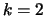
we illustrate the equivalence with Definition
11.3: From
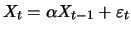
we
directly obtain
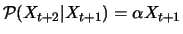
with
From the
'backward regression'
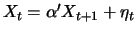
with
white noise
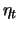
it further follows that
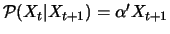
with
For
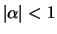
the process is covariance-stationary and it holds
that
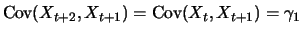
and
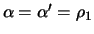
. We obtain
and
With this we get for the partial autocorrelation of 2nd order
which corresponds to the results in (
11.18). For the
AR(1) process it holds that
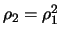
and thus
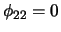
.
It holds in general for AR(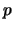 ) processes that
) processes that
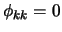 for
all
for
all 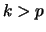 . In Figure 11.5 the PACF of an AR(2)
process is displayed using the parameters as in Figure
11.4.
. In Figure 11.5 the PACF of an AR(2)
process is displayed using the parameters as in Figure
11.4.
Fig.:
PACF of an AR(2) process with
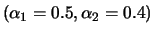 (top left),
(top left),
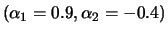 (top right),
(top right),
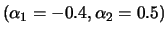 (bottom left) and
(bottom left) and
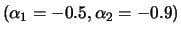 (bottom right).
(bottom right).
 SFEpacfar2.xpl
SFEpacfar2.xpl
|
|
Example 12.4 (MA(1))
For a MA(1) process
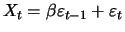
with
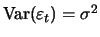
it holds that
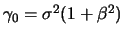
,
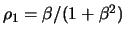
and
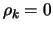
for all
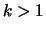
. For the partial autocorrelations we
obtain
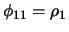
and
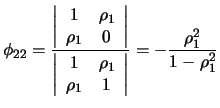 |
(12.19) |
For a MA(1) process it strictly holds that
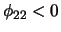
. If one
were to continue the calculation with
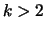
, one could determine
that the partial autocorrelations will not reach zero.
Figure 11.6 shows the PACF of a MA(2) process. In
general for a MA(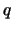 ) process it holds that the PACF does not
decay, in contrast to the autoregressive process. Compare the PACF
to the ACF in Figure 11.2. This is thus a possible
criterium for the specification of a linear model.
) process it holds that the PACF does not
decay, in contrast to the autoregressive process. Compare the PACF
to the ACF in Figure 11.2. This is thus a possible
criterium for the specification of a linear model.
Fig.:
PACF of a MA(2) process with
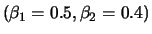 (top left),
(top left),
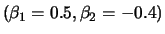 (top right),
(top right),
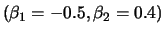 (bottom left) and
(bottom left) and
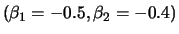 (bottom right).
(bottom right).
 SFEpacfma2.xpl
SFEpacfma2.xpl
|
|
![]() and
and
![]() is to
filter out of
is to
filter out of ![]() and
and
![]() the linear influence of the
random variables that lie in between,
the linear influence of the
random variables that lie in between,
![]() and then calculate the correlation
of the transformed random variables. This is called the partial autocorrelation.
and then calculate the correlation
of the transformed random variables. This is called the partial autocorrelation.
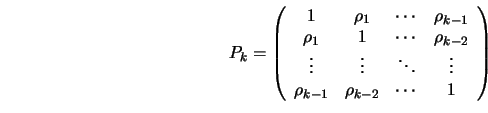
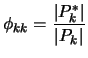
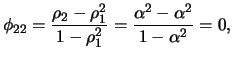
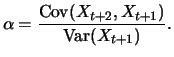
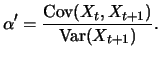
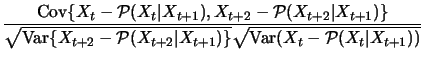
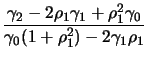
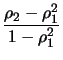
![]() ) processes that
) processes that
![]() for
all
for
all ![]() . In Figure 11.5 the PACF of an AR(2)
process is displayed using the parameters as in Figure
11.4.
. In Figure 11.5 the PACF of an AR(2)
process is displayed using the parameters as in Figure
11.4.
![\includegraphics[width=0.5\defpicwidth]{pacfar21.ps}](sfehtmlimg2145.gif)
![\includegraphics[width=0.5\defpicwidth]{pacfar22.ps}](sfehtmlimg2146.gif)
![\includegraphics[width=0.5\defpicwidth]{pacfar23.ps}](sfehtmlimg2147.gif)
![\includegraphics[width=0.5\defpicwidth]{pacfar24.ps}](sfehtmlimg2148.gif)
![\includegraphics[width=0.5\defpicwidth]{pacfma21.ps}](sfehtmlimg2156.gif)
![\includegraphics[width=0.5\defpicwidth]{pacfma22.ps}](sfehtmlimg2157.gif)
![\includegraphics[width=0.5\defpicwidth]{pacfma23.ps}](sfehtmlimg2158.gif)
![\includegraphics[width=0.5\defpicwidth]{pacfma24.ps}](sfehtmlimg2159.gif)