![\includegraphics[width=1\defpicwidth]{wr.ps}](sfehtmlimg2289.gif)
|
In addition a far-reaching agreement has been formed that returns cannot be regarded as i.i.d. and at most as being uncorrelated. This argument holds at least for financial time series of relatively high frequency, for example for daily data. In Figure 12.1 we show a normally distributed white noise, a GARCH(1,1) process in Figure 12.2 and the DAFOX index (1993-96) in Figure 12.3, see http://finance.wiwi.uni-karlsruhe.de/Forschung/dafox.html . It can be seen from the figure that the GARCH process is obviously more appropriate for modelling stock returns than white noise.
However the ARCH model is only the starting point of the empirical study and relies on a wide range of specification tests. Some practically relevant disadvantages of the ARCH model have been discovered recently, for example, the definition and modelling of the persistence of shocks and the problem of modelling asymmetries. Thus a large number of extensions of the standard ARCH model have been suggested. We will discuss them in detail later.
Let ![]() be a discrete stochastic process and from Definition
10.15
be a discrete stochastic process and from Definition
10.15
![]() the relative
increase or the return of the process
the relative
increase or the return of the process ![]() . If the returns
are independent and identically distributed, then
. If the returns
are independent and identically distributed, then ![]() follows a
geometric random walk. It is assumed in ARCH models that the
returns depend on past information with a specific form.
follows a
geometric random walk. It is assumed in ARCH models that the
returns depend on past information with a specific form.
As mentioned before
![]() denotes the information set at
time
denotes the information set at
time ![]() , which encompasses
, which encompasses ![]() and all the past realizations of
the process
and all the past realizations of
the process ![]() . This means in a general model
. This means in a general model
| (13.1) |
The ARCH model of order 1, ARCH(1), is defined as follows:
where
Setting
![]() , it holds for the semi-strong
and the strong ARCH models that
, it holds for the semi-strong
and the strong ARCH models that
![]() and
and
![]() . In
strong ARCH models
. In
strong ARCH models ![]() is i.i.d. so that no dependence can be
modelled in higher moments than the second moment. It is
frequently assumed that
is i.i.d. so that no dependence can be
modelled in higher moments than the second moment. It is
frequently assumed that ![]() is normally distributed, which means
is normally distributed, which means
![]() is conditionally normally distributed:
is conditionally normally distributed:
Originally only strong and semi-strong ARCH models are discussed in the literature. Weak ARCH models are important because they are closed under temporal aggregation. If, for example, daily returns follow a weak ARCH process, then the weekly and monthly returns are also weak ARCH with corresponding parameter adjustments. This phenomenon holds in general for strong and semi-strong models.
According to Definition 12.1 the process
![]() is a martingale difference and therefore white
noise.
is a martingale difference and therefore white
noise.
If the innovation
![]() is symmetrically
distributed around zero, then all odd moments of
is symmetrically
distributed around zero, then all odd moments of
![]() are equal to zero. Under the assumption of normal distribution
(12.3) the conditions for the existence of higher even
moments can be derived.
are equal to zero. Under the assumption of normal distribution
(12.3) the conditions for the existence of higher even
moments can be derived.
![$\displaystyle \mathop{\text{\rm\sf E}}[\varepsilon_t^4]=\frac{3\omega^2}{(1-\alpha)^2}\frac{1-\alpha^2}{1-3\alpha^2}
$](sfehtmlimg2315.gif)
![$\displaystyle \mathop{\text{\rm Kurt}}(\varepsilon_t) = \frac{\mathop{\text{\rm...
...\text{\rm\sf E}}[\varepsilon_t^2]^2} =
3 \frac{1-\alpha^2}{1-3\alpha^2} \ge 3.
$](sfehtmlimg2320.gif)
For the boundary case
![]() and the normally distributed
innovations
and the normally distributed
innovations
![]() , while for
, while for
![]() it holds that
it holds that
![]() . The unconditional distribution
is also leptokurtic under conditional heteroscedasticity, i.e.,
the curvature is high in the middle of the distribution and the
tails are fatter than those of a normal distribution, which is
frequently observed in financial markets.
. The unconditional distribution
is also leptokurtic under conditional heteroscedasticity, i.e.,
the curvature is high in the middle of the distribution and the
tails are fatter than those of a normal distribution, which is
frequently observed in financial markets.
The thickness of the tails and thus the existence of moments
depend on the parameters of the ARCH models. The variance of the
ARCH(1) process is finite when ![]() (Theorem
12.2), while the fourth moment in the case
of normally distributed error terms exists when
(Theorem
12.2), while the fourth moment in the case
of normally distributed error terms exists when
![]() (Theorem 12.3). Already in the sixties
Mandelbrot had questioned the existence of the variance of several
financial time series. Frequently empirical distributions have so
fat tails that one can not conclude a finite variance. In order to
make empirical conclusions on the degree of the tail's thickness
of the unconditional distribution, one can assume, for example,
that the distribution is a Pareto type, i.e., for large
(Theorem 12.3). Already in the sixties
Mandelbrot had questioned the existence of the variance of several
financial time series. Frequently empirical distributions have so
fat tails that one can not conclude a finite variance. In order to
make empirical conclusions on the degree of the tail's thickness
of the unconditional distribution, one can assume, for example,
that the distribution is a Pareto type, i.e., for large ![]() :
:
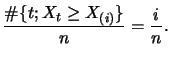
![\includegraphics[width=1\defpicwidth]{taildax.ps}](sfehtmlimg2339.gif)
|
Hill (1975) has suggested an estimator using the maximum likelihood method:
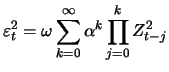
![$\displaystyle \mathop{\text{\rm\sf E}}[\varepsilon_t^2 - \omega \sum_{k=0}^m \alpha^k \prod_{j=0}^k Z_{t-j}^2]$](sfehtmlimg2347.gif) |
![$\displaystyle \alpha^{m+1} \mathop{\text{\rm\sf E}}[\varepsilon_{t-m-1}^2 \prod_{j=0}^{m} Z_{t-j}^2]$](sfehtmlimg2348.gif) |
||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
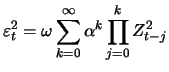
![$\displaystyle \mathop{\text{\rm\sf E}}[(\varepsilon_t^2 - \omega \sum_{k=0}^m \alpha^k \prod_{j=0}^k Z_{t-j}^2)^2]$](sfehtmlimg2357.gif) |
![$\displaystyle \mathop{\text{\rm\sf E}}[(\alpha^{m+1} \varepsilon_{t-m-1}^2 \prod_{j=0}^{m} Z_{t-j}^2)^2]$](sfehtmlimg2358.gif) |
||
| 0 for |
The dynamics of the volatility process in the case of ARCH(1) is
essentially determined by the parameter ![]() . In Theorem
12.5 it was shown that the square of an ARCH(1)
process follows an AR(1) process. The correlation structure of the
empirical squared observations of returns are frequently more
complicated than a simple AR(1) process. In Section
12.1.3 we will consider an ARCH model of order
. In Theorem
12.5 it was shown that the square of an ARCH(1)
process follows an AR(1) process. The correlation structure of the
empirical squared observations of returns are frequently more
complicated than a simple AR(1) process. In Section
12.1.3 we will consider an ARCH model of order ![]() with
with
![]() , which allows a more flexible modelling of the correlation
structure.
, which allows a more flexible modelling of the correlation
structure.
The volatility is a function of the past squared observations in
ARCH models in a narrow sense. In the more general GARCH models
(Section 12.1.5) it may depend on the past squared
volatilities in addition. These models belong to the large group
of unpredictable time series with stochastic volatility.
In the strong form, they have
![]() where
where
![]() is
is
![]() -measurable, i.e. the volatility
-measurable, i.e. the volatility
![]() depends only on the information to the time point
depends only on the information to the time point ![]() and the i.i.d. innovations
and the i.i.d. innovations ![]() with
with
![]() .
For such a time series it holds
.
For such a time series it holds
![]() ,
i.e.
,
i.e.
![]() is unpredictable and, except in the special
case that
is unpredictable and, except in the special
case that
![]() const.
const.![]() conditionally heteroscedastic. The stylized facts 2-4
are only fulfilled under certain qualitative assumptions. For
example, in order to produce volatility cluster
conditionally heteroscedastic. The stylized facts 2-4
are only fulfilled under certain qualitative assumptions. For
example, in order to produce volatility cluster ![]() must
tend to be large when the squared observations or volatilities of
the recent past observations are large. The generalizations of the
ARCH models observed in this section fulfill the corresponding
conditions.
must
tend to be large when the squared observations or volatilities of
the recent past observations are large. The generalizations of the
ARCH models observed in this section fulfill the corresponding
conditions.
This result is often used reversely in order to estimate the
parameter of financial models in the continuous time where one
approximates the corresponding diffusion processes through
discrete GARCH time series and estimates its parameter.
Nelson (1990![]() ) shows only the convergence of GARCH
processes against diffusion processes in a weak sense (convergence
on the distribution). A recent work of Wang (2002)
shows however that the approximation does not hold in a stronger
sense, especially the likelihood process is not asymptotically
equivalent. In this sense the maximum likelihood estimators for
the discrete time series do not converge against the parameters of
the diffusion limit process.
) shows only the convergence of GARCH
processes against diffusion processes in a weak sense (convergence
on the distribution). A recent work of Wang (2002)
shows however that the approximation does not hold in a stronger
sense, especially the likelihood process is not asymptotically
equivalent. In this sense the maximum likelihood estimators for
the discrete time series do not converge against the parameters of
the diffusion limit process.
Theorem 12.5 says that an ARCH(1) process can be
represented as an AR(1) process in ![]() . A simple Yule-Walker
estimator uses this property:
. A simple Yule-Walker
estimator uses this property:
The estimation of ARCH models is normally done using the maximum
likelihood (ML) method. Assuming that the returns
![]() have a conditionally normal distribution, we have:
have a conditionally normal distribution, we have:
Figure 12.5 shows the conditional likelihood of a
generated ARCH(1) process with ![]() . The parameter
. The parameter ![]() is
chosen so that the unconditional variance is everywhere constant,
i.e., with a variance of
is
chosen so that the unconditional variance is everywhere constant,
i.e., with a variance of ![]() ,
,
![]() .
The optimization of the likelihood of an ARCH(1) model can be
found by analyzing the graph. Most often we would like to know the
precision of the estimator as well. Essentially it is determined
by the second derivative of the likelihood at the optimization
point by the asymptotic properties of the ML estimator (see
Section 12.1.6). Furthermore one has to use numerical
methods such as the score algorithm introduced in Section
11.8 to estimate the parameters of the models with a
larger order. In this case the first and second partial
derivatives of the likelihood must be calculated.
.
The optimization of the likelihood of an ARCH(1) model can be
found by analyzing the graph. Most often we would like to know the
precision of the estimator as well. Essentially it is determined
by the second derivative of the likelihood at the optimization
point by the asymptotic properties of the ML estimator (see
Section 12.1.6). Furthermore one has to use numerical
methods such as the score algorithm introduced in Section
11.8 to estimate the parameters of the models with a
larger order. In this case the first and second partial
derivatives of the likelihood must be calculated.
![\includegraphics[width=1\defpicwidth]{likarch1.ps}](sfehtmlimg2399.gif)
|
With the ARCH(1) model these are
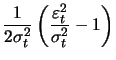 |
(13.10) | ||
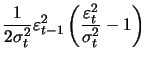 |
(13.11) | ||
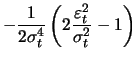 |
(13.12) | ||
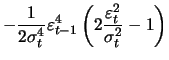 |
(13.13) | ||
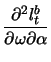 |
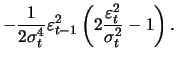 |
(13.14) |
![$\displaystyle \mathop{\text{\rm\sf E}}\left[ \frac{\partial^2 l_t^b}{\partial \...
...ight] = -\frac{1}{2}\mathop{\text{\rm\sf E}}\left[\frac{1}{\sigma_t^4}\right].
$](sfehtmlimg2414.gif)
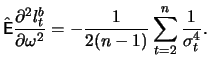
![$\displaystyle \mathop{\text{\rm\sf E}}\left[ \frac{\partial^2 l_t^b}{\partial \...
...{2}\mathop{\text{\rm\sf E}}\left[\frac{\varepsilon_{t-1}^4}{\sigma_t^4}\right]
$](sfehtmlimg2418.gif)
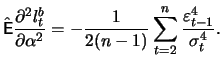
Proof:
![$ \mathop{\text{\rm\sf E}}\left[\left(\frac{\partial
l_t^b}{\partial \omega}\rig...
...\mathop{\text{\rm\sf E}}
\left[\frac{1}{4\sigma_t^4} (Z_t^4 - 2Z_t^2+1)\right]
$](sfehtmlimg2421.gif)
Obviously Theorem 12.6 also holds for the
parameter ![]() in place of
in place of ![]() . In addition it
essentially holds for more general models, for example the
estimation of GARCH models in Section 12.1.6. In more
complicated models one can replace the second derivative with the
square of the first derivative, which is easier to calculate. It
is assumed, however, that the likelihood function is correctly
specified, i.e., the true distribution of the error terms is
normal.
. In addition it
essentially holds for more general models, for example the
estimation of GARCH models in Section 12.1.6. In more
complicated models one can replace the second derivative with the
square of the first derivative, which is easier to calculate. It
is assumed, however, that the likelihood function is correctly
specified, i.e., the true distribution of the error terms is
normal.
Under the two conditions
| (13.15) |
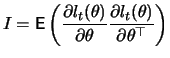
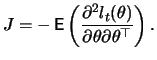
If the true distribution of ![]() is normal, then
is normal, then ![]() and the
asymptotic covariance matrix is simplified to
and the
asymptotic covariance matrix is simplified to ![]() , i.e., the
inverse of the Fischer Information matrix. If the true
distribution is instead leptokurtic, then the maximum of
(12.9) is still consistent, but no longer efficient.
In this case the ML method is interpreted as the `Quasi Maximum
Likelihood' (QML) method.
, i.e., the
inverse of the Fischer Information matrix. If the true
distribution is instead leptokurtic, then the maximum of
(12.9) is still consistent, but no longer efficient.
In this case the ML method is interpreted as the `Quasi Maximum
Likelihood' (QML) method.
In a Monte Carlo simulation study in Shephard (1996) 1000
ARCH(1) processes with
![]() and
and
![]() were
generated and the parameters were estimated using QML. The results
are given in Table 12.2. Obviously with the moderate
sample sizes (
were
generated and the parameters were estimated using QML. The results
are given in Table 12.2. Obviously with the moderate
sample sizes (![]() ) the bias is negligible. The variance,
however, is still so large that a relatively large proportion
(10%) of the estimators are larger than one, which would imply
covariance nonstationarity. This, in turn, has a considerable
influence on the volatility prediction.
) the bias is negligible. The variance,
however, is still so large that a relatively large proportion
(10%) of the estimators are larger than one, which would imply
covariance nonstationarity. This, in turn, has a considerable
influence on the volatility prediction.
|
The definition of an ARCH(1) model will be extended for the case
that ![]() lags, on which the conditional variance depends.
lags, on which the conditional variance depends.
The conditional variance
![]() in an ARCH(
in an ARCH(![]() ) model is
also a linear function of the
) model is
also a linear function of the ![]() squared lags.
squared lags.
If instead
![]() , then the
unconditional variance does not exist and the process is not
covariance-stationary.
, then the
unconditional variance does not exist and the process is not
covariance-stationary.
It is problematic with the ARCH(![]() ) model that for some
applications a larger order
) model that for some
applications a larger order ![]() must be used, since large lags
only lose their influence on the volatility slowly. It is
suggested as an empirical rule of thumb to use a minimum order of
must be used, since large lags
only lose their influence on the volatility slowly. It is
suggested as an empirical rule of thumb to use a minimum order of
![]() . The disadvantage of a large order is that many parameters
have to be estimated under restrictions. The restrictions can be
categorized as conditions for stationarity and the strictly
positive parameters. If efficient estimation methods are to be
used, for example, the maximum likelihood method, the estimation
of large dimensional parameter spaces can be numerically quite
complicated to obtain.
. The disadvantage of a large order is that many parameters
have to be estimated under restrictions. The restrictions can be
categorized as conditions for stationarity and the strictly
positive parameters. If efficient estimation methods are to be
used, for example, the maximum likelihood method, the estimation
of large dimensional parameter spaces can be numerically quite
complicated to obtain.
One possibility of reducing the number of parameters while including a long history is to assume linearly decreasing weights on the lags, i.e.,
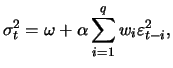
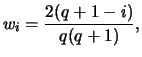
For the general ARCH(![]() ) model from (12.16) the
conditional likelihood is
) model from (12.16) the
conditional likelihood is
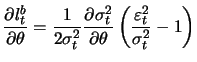 |
(13.18) |
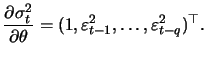
The ARCH(![]() ) model can be generalized by
extending it with autoregressive terms of the volatility.
) model can be generalized by
extending it with autoregressive terms of the volatility.
The sufficient but not necessary conditions for
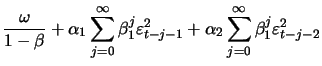 |
|||
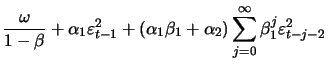 |
If
![]() follows a GARCH process, then from Theorem
12.9 we can see that
follows a GARCH process, then from Theorem
12.9 we can see that
![]() follows an
ARMA model with conditional heteroscedastic error
terms
follows an
ARMA model with conditional heteroscedastic error
terms ![]() . As we know if all the roots of the polynomial
. As we know if all the roots of the polynomial
![]() lie outside the unit circle,
then the ARMA process (12.21) is invertible and can
be written as an AR(
lie outside the unit circle,
then the ARMA process (12.21) is invertible and can
be written as an AR(![]() ) process. Moveover it follows from
Theorem 12.8 that the GARCH(
) process. Moveover it follows from
Theorem 12.8 that the GARCH(![]() ) model
can be represented as an ARCH(
) model
can be represented as an ARCH(![]() ) model. Thus one can deduce
analogous conclusions from the ARMA models in determining the
order
) model. Thus one can deduce
analogous conclusions from the ARMA models in determining the
order ![]() of the model. There are however essential
differences in the definition of the persistence of shocks.
of the model. There are however essential
differences in the definition of the persistence of shocks.
General conditions for the existence of higher moments of the
GARCH(![]() ) models are given in He and Teräsvirta (1999). For the
smaller order models and under the assumption of distribution we
can derive:
) models are given in He and Teräsvirta (1999). For the
smaller order models and under the assumption of distribution we
can derive:
The function (12.22) is illustrated in Figure
12.6 for all
![]() ,
,
![]() ,
i.e., the distribution of
,
i.e., the distribution of
![]() is leptokurtic. We can
observe that the kurtosis equals 3 only in the case of the
boundary value
is leptokurtic. We can
observe that the kurtosis equals 3 only in the case of the
boundary value
![]() where the conditional
heteroscedasticity disappears and a Gaussian white noise takes
place. In addition it can be seen in the figure that the kurtosis
increases in
where the conditional
heteroscedasticity disappears and a Gaussian white noise takes
place. In addition it can be seen in the figure that the kurtosis
increases in ![]() slowly for a given
slowly for a given ![]() . On the
contrary it increases in
. On the
contrary it increases in ![]() much faster for a given
much faster for a given
![]() .
.
![\includegraphics[width=1.2\defpicwidth]{kurgarch.ps}](sfehtmlimg2493.gif)
|
In practical applications it is frequently shown that models with smaller order sufficiently describe the data. In most cases GARCH(1,1) is sufficient.
A substantial disadvantage of the standard ARCH and GARCH models exists since they can not model asymmetries of the volatility with respect to the sign of past shocks. This results from the squared form of the lagged shocks in (12.16) and (12.19). Therefore they have an effect on the level but no effect on the sign. In other words, bad news (identified by a negative sign) has the same influence on the volatility as good news (positive sign) if the absolute values are the same. Empirically it is observed that bad news has a larger effect on the volatility than good news. In Section 12.2 and 13.1 we will take a closer look at the extensions of the standard models which can be used to calculate these observations.
Based on the ARMA representation of GARCH processes (see Theorem
12.9) Yule-Walker estimators
![]() are
considered once again. These estimators are, as can be shown,
consistent and asymptotically normally distributed,
are
considered once again. These estimators are, as can be shown,
consistent and asymptotically normally distributed,
![]() . However in the case
of GARCH models they are not efficient in the sense that the
matrix
. However in the case
of GARCH models they are not efficient in the sense that the
matrix
![]() is positively definite,
where
is positively definite,
where
![]() is the asymptotic covariance matrix of the
QML estimator, see (12.25). In the literature there are
several experiments on the efficiency of the Yule-Walker and QML
estimators in finite samples, see Section 12.4. In
most cases maximum likelihood methods are chosen in order to get
the efficiency.
is the asymptotic covariance matrix of the
QML estimator, see (12.25). In the literature there are
several experiments on the efficiency of the Yule-Walker and QML
estimators in finite samples, see Section 12.4. In
most cases maximum likelihood methods are chosen in order to get
the efficiency.
The likelihood function of the general GARCH(![]() ) model
(12.19) is identical to (12.17) with the
extended parameter vector
) model
(12.19) is identical to (12.17) with the
extended parameter vector
![]() . Figure 12.7
displays the likelihood function of a generated GARCH(1,1) process
with
. Figure 12.7
displays the likelihood function of a generated GARCH(1,1) process
with
![]() ,
,
![]() ,
, ![]() and
and ![]() . The
parameter
. The
parameter ![]() was chosen so that the unconditional variance
is everywhere constant, i.e., with a variance of
was chosen so that the unconditional variance
is everywhere constant, i.e., with a variance of ![]() ,
,
![]() . As one can see, the function is
flat on the right, close to the optimum, thus the estimation will
be relatively imprecise, i.e., it will have a larger variance. In
addition, Figure 12.8 displays the contour plot of
the likelihood function.
. As one can see, the function is
flat on the right, close to the optimum, thus the estimation will
be relatively imprecise, i.e., it will have a larger variance. In
addition, Figure 12.8 displays the contour plot of
the likelihood function.
![\includegraphics[width=1.0\defpicwidth]{likgar3d.ps}](sfehtmlimg2504.gif)
|
![\includegraphics[width=1\defpicwidth]{likgarco.ps}](sfehtmlimg2505.gif)
|
The first partial derivatives of (12.17) are
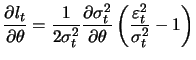 |
(13.23) |
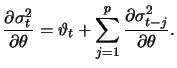
Under the conditions
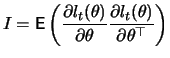
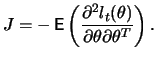
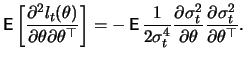
![$\displaystyle \mathop{\text{\rm\sf E}}\left[\frac{\partial l_t(\theta)}{\partial \theta}\frac{\partial l_t(\theta)}{\partial \theta^{T}}\right]$](sfehtmlimg2518.gif) |
![$\displaystyle \mathop{\text{\rm\sf E}}\left[ \frac{1}{4\sigma_t^4} \frac{\parti...
...l \theta}
\frac{\partial \sigma_t^2}{\partial \theta^T}
(Z_t^4-2Z_t^2+1)\right]$](sfehtmlimg2519.gif) |
(13.26) | |
![$\displaystyle \mathop{\text{\rm\sf E}}\left[ \frac{1}{4\sigma_t^4} \frac{\parti...
...al
\theta^\top }\right] \{\mathop{\text{\rm Kurt}}(Z_t \mid {\cal
F}_{t-1})-1\}$](sfehtmlimg2520.gif) |
If the distribution of ![]() is specified correctly, then
is specified correctly, then ![]() and the asymptotic variance can be simplified to
and the asymptotic variance can be simplified to ![]() , i.e.,
the inverse of the Fisher Information matrix. If this is not the
case and it is instead leptokurtic, for example, the maximum of
(12.9) is still consistent but no longer efficient.
In this case the ML method is interpreted as the `Quasi Maximum
Likelihood' (QML) method.
, i.e.,
the inverse of the Fisher Information matrix. If this is not the
case and it is instead leptokurtic, for example, the maximum of
(12.9) is still consistent but no longer efficient.
In this case the ML method is interpreted as the `Quasi Maximum
Likelihood' (QML) method.
Consistent estimators for the matrices ![]() and
and ![]() can be obtained
by replacing the expectation with the simple average.
can be obtained
by replacing the expectation with the simple average.