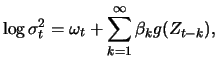13.2 Extensions of the GARCH Model

Standard GARCH models assume that positive and negative error terms have a symmetric effect on the volatility. In other words, good and bad news have the same effect on the volatility in this model. In practice this assumption is frequently violated, in particular by stock returns, in that the volatility increases more after bad news than after good news. This so called Leverage Effect appears firstly in Black (1976), who noted that:

``a drop in the value of the firm will cause a negative return on its stock, and will usually increase the leverage of the stock. [...] That rise in the debt-equity ratio will surely mean a rise in the volatility of the stock''.

A very simple but plausible explanation for the leverage effect: Negative returns imply a larger proportion of debt through a reduced market value of the firm, which leads to a higher volatility. The risk, i.e. the volatility reacts first to larger changes of the market value, nevertheless it is empirically shown that there is a high volatility after smaller changes. On the other hand, Black said nothing about the effect of positive returns on the volatility. Although the positive returns cause smaller increases, they do cause an increase in the volatility. From an empirical point of view the volatility reacts asymmetrically to the sign of the shocks and therefore a number of parameterized extensions of the standard GARCH model have been suggested recently. In the following we will discuss two of the most important ones: the exponential GARCH (EGARCH) and the threshold GARCH (TGARCH) model.

13.2.1 Exponential GARCH

Let $Z_t$ further denote a series of $i.i.d.$ standardized random variables with expectation 0 and variance 1. The general exponential GARCH (EGARCH) model is given by Nelson (1991):

$$\log \sigma_t^2 = \omega_t + \sum_{k=1}^{\infty} \beta_k g(Z_{t-k}),$$ (13.27)

where $\omega_t$, $\beta_k$ are deterministic coefficients and

$$g(Z_t) = \theta Z_t + \gamma( \vert Z_t\vert - E\vert Z_t\vert ).$$ (13.28)

It can be directly seen that $E\left[g(Z_t)\right] = 0$.

The EGARCH model in (12.27) shows some differences from the standard GARCH model:

• Volatility of the EGARCH model, which is measured by the conditional variance $\sigma_t^2$, is an explicit multiplicative function of lagged innovations. On the contrary, volatility of the standard GARCH model is an additive function of the lagged error terms $\varepsilon_t$, which causes a complicated functional dependency on the innovations; for example the ARCH(1) in Theorem 12.4.
• Volatility can react asymmetrically to the good and bad news.
• For the general distributions of $Z_t$ the parameter restrictions for strong and covariance-stationarity coincide.
• The parameters in (12.27) and (12.28) are not restricted to positive values.

The function $g(\cdot)$ in (12.28) is piecewise linear. It contains two parameters which define the `size effect' and the `sign effect' of the shocks on volatility. The first is a typical ARCH effect while the second is an asymmetrical effect, for example, the leverage effect. The term $\gamma(\vert Z_t\vert - E\vert Z_t\vert)$ determines the size effect and the term $\theta Z_t$ determines the sign effect. The parameter $\gamma$ is thus typically positive and $\theta$ is negative.

To estimate EGARCH models instead of the general MA($\infty$) representation (12.27), an ARMA($p,q$) model is applied, i.e.,

$$\Delta(L) \log \sigma_t^2 = \omega + \Psi(L) g(Z_t),$$ (13.29)

with lag-polynomial $\Delta(L)$ and $\Psi(L)$ of order $p$ and $q$ respectively.

EGARCH models benefit from no parameter restrictions, thus the possible instabilities of optimization routines are reduced. On the other hand the theoretical properties of QML estimators of EGARCH models are not clarified to a great extent.

Let $\omega_t=\omega=0$ and $\sum_{k=1}^{\infty}\beta_k^2 < \infty$. Then $\sigma_t^2$ is strictly stationary and ergodic, see Theorem 2.1 in Nelson (1991). Furthermore, under these conditions the unconditional variance exists when $Z_t$ has a generalized error distribution (GED) with parameter $\zeta > 1$, which determines the thickness of the tails, see Theorem 2.2 in Nelson (1991). The GED is leptokurtic when $\zeta<2$.

The normal distribution is a special case of the GED ($\zeta=2$). Nelson gives in addition complicated formulas of the unconditional moments. One problem is that under other leptokurtic distributions such as the Student-$t$, the unconditional variance does not exist. The reason is that exponential growth of the conditional variance changes with the level of the shocks, which leads to the explosion of the unconditional variance when the probability for extreme shocks is sufficiently large. Therefore the existence of the unconditional moments depends on the choice of the distribution of the innovations, which is an undesirable property of the EGARCH models. In empirical studies it has been found that EGARCH often overweighs the effects of larger shocks on volatility and thus results in poorer fits than standard GARCH models, see the empirical studies of Engle and Ng (1993).

13.2.2 Threshold ARCH Models

The idea of the Threshold ARCH (TARCH) models is to divide the distribution of the innovations into disjoint intervals and then approximate a piecewise linear function for the conditional standard deviation, see Zakoian (1991), and the conditional variance respectively, see Glosten et al. (1993). If there are only two intervals, the division is normally at zero, i.e., the influence of positive and negative innovations on the volatility is differentiated. In this case the TARCH model of order $q$ can be written as

$$\sigma_t^\delta = \omega + \sum_{i=1}^q \alpha_i \varepsilon_{t-i... ...lta + \sum_{i=1}^q \alpha_i^- \varepsilon_{t-i}^\delta I(\varepsilon_{t-i}< 0),$$ (13.30)

with the indicator function $I(\cdot)$ and $\delta=1$ as in Zakoian (1991) or $\delta=2$ as in Glosten et al. (1993).

Rabemananjara and Zakoian (1993) extend this model by including the lagged conditional standard deviations (variance respectively) as a regressor, which is known as the TGARCH model. They also give conditions for covariance-stationarity in their study.

Instead of a piecewise linear function Gouriéroux and Monfort (1992) use a stepwise function (piecewise constant) as a model for the volatility. Let $A_j, j=1,\ldots,J$ be a partition of the distribution of the innovation. Then a qualitative threshold ARCH model (QTARCH) of order 1 is given by:

$$y_t = \sum_{j=1}^J m_j I(y_{t-1} \in A_j)+ \sum_{j=1}^J s_j I(y_{t-1} \in A_j) Z_t,$$ (13.31)

where $m_j$ and $s_j$ are scalars. In (12.31) conditional expectations and conditional standard deviations are modelled as stepwise functions. One notices that (12.31) is a homogenous Markov Chain of order one. Models of higher order can be easily derived. Gouriéroux and Monfort (1992) give a detailed discussion of the statistical properties of (12.31). Moreover the consistency and asymptotic normal distribution of the QML estimators are also discussed by them.

The threshold models are identified by an abrupt transition between two regimes when the generating innovation crosses a threshold value. If a smooth transition is preferred in the model, then the indicator function in (12.30) can be replaced with the desired continuous function, which tends to zero if the values are close to $\varepsilon_{t-i}$ and tends to one for the values further away. Frequently, the logistic function is chosen. The model is thus

$$\sigma_t^\delta = \omega + \sum_{i=1}^q \alpha_i \varepsilon_{t-i}^\delta + \sum_{i=1}^q \alpha_i^- \varepsilon_{t-i}^\delta F_\gamma(\varepsilon_{t-i})$$ (13.32)

$$F_\gamma(u) = \frac{1}{1+\exp(-\gamma u)},$$ (13.33)

with the parameter $\gamma>0$. The indicator function is a limiting case of the logistic function for $\gamma \longrightarrow \infty$.

Finally, another model class needs to be mentioned, which is very general and can replicate the asymmetries: the Asymmetric Power ARCH (APARCH) model from Ding et al. (1993),

$$\sigma_t^\delta = \omega + \sum_{i=1}^q \alpha_i (\vert\varepsilo... ...-\gamma_i \varepsilon_{t-i})^\delta + \sum_{j=1}^p \beta_j \sigma_{t-j}^\delta,$$ (13.34)

where $\delta>0$ is a parameter to be estimated. However note that the EGARCH model is not included in this model class, a direct test between GARCH and EGARCH models is thus impossible. A very general ARCH model, the augmented GARCH model from Duan (1997), also includes the EGARCH model.

13.2.3 Risk and Returns

In finance theory the relationship between risk and returns plays an important role. Many theoretical models such as CAPM, imply a linear relationship between the expected returns of a market portfolio and the variance. If the risk (i.e. the variance) is not constant over time, then the conditional expectation of the market returns is a linear function of the conditional variance. The idea from Engle et al. (1987) was consequently used to estimate the conditional variances in GARCH and then the estimations will be used in the conditional expectations' estimation. This is the so called ARCH in Mean (ARCH-M) model.

Let $y_t$ be a covariance-stationary return process of a broad market index and $\sigma_t^2$ be the conditional variance specified in an ARCH(1) model. The ARCH-M model is

$$y_t = \nu + \lambda g(\sigma_t^2) + \varepsilon_t$$ (13.35)

$$\sigma_t^2 = \omega + \alpha \varepsilon_{t-1}^2,$$

where $g(\cdot)$ is a known parameter function. The CAPM implies that $g(x)=x$, although in most empirical applications the square root or the logarithm is used. The expression $\lambda g(\sigma_t^2)$ can be interpreted as the risk premium.

13.2.4 Estimation Results for the DAX Returns

We applied various ARCH models discussed before to the returns of the German stock index (DAX). Here we didn't use the DAX as quoted on the stock exchange, but instead the DAFOX from the capital market database in Karlsruhe, which has been created for analysis purposes and is adjusted for dividends and inflation. We consider daily returns from 1974 to 1996 (5748 observations).

The returns indicate a clear autocorrelation of first order. There are various possibilities to model these autocorrelations. Two most important models, which we have discussed, are the AR models and the ARCH-M models. The latter is easy to be interpreted economically, i.e., a time dependent risk premium implying an autocorrelation of the returns. This economic motivation is missing for the AR models: the AR term cannot be interpreted as the risk premium, since it can be negative, which contradicts the usual assumption of a risk averse agent. However the AR models offer frequently a better fit to the data than ARCH-M model. The basic model is thus

$$y_t = \mu_t + \sigma_t Z_t$$

with $\mu_t = \nu + \phi y_{t-1}$ (AR(1)) respectively $\mu_t = \nu + \lambda \sigma_t$ (ARCH-M), and $\sigma_t$ can be GARCH, TGARCH or EGARCH.

The estimation results are given in Table 12.3. They can be summarized as follows:

• The parameter $\nu$ is significantly positive for all AR models, which is reflected in the long-run increasing trend of the stock price. For the ARCH-M model the sign of the trends is not only given in $\nu$ but also in $\lambda$. The effect of a negative $\nu$ can be dominated by a positive $\lambda$, which is the case in the GARCH-M and the EGARCH-M models.
• The ARCH effects are very pronounced, i.e., the parameter $\alpha$ in the GARCH model is significant.
• There is a high persistence of shocks in the volatility. This persistence is measured in the GARCH case by the sum of $\alpha$ and $\beta$ and is in each case close to 1.
• Except for the EGARCH specification of the volatility the AR(1) model describes the data better than the ARCH-M models.
• There exists a leverage effect: the corresponding parameters in the TGARCH and the EGARCH models have the appropriate signs. In the TGARCH case the $t$-statistic for $\alpha^-$ is 1.75 and 1.77 respectively, and in the EGARCH case the $t$-statistic for $\theta$ is -3.65 and -1.97 respectively. Negative shocks increase the volatility more than positive shocks.
• The TGARCH and the EGARCH models have a priority for asymmetry, since they have a better fit to the data when the same number of parameters are considered.

Table 12.3: Estimation results of various ARCH models, applied to DAFOX returns 1974-1996. In the parenthesis is the $t$-statistic based on the QML asymptotic standard error.

	AR-G	AR-TG	AR-EG	GARCH-M	TGARCH-M	EGARCH-M
$\lambda$				0.107	0.051	0.338
				(2.14)	(1.09)	(3.31)
$\nu$	3.75E-04	3.03E-04	2.57E-04	-2.84E-04	4.71E-05	-0.002
	(4.414)	(3.290)	(2.608)	(-0.79)	(0.14)	(-2.72)
$\phi$	0.131	0.137	0.136
	(6.808)	(8.079)	(5.940)
$\omega$	8.42E-07	8.22E-07	-5.259	8.81E-07	8.78E-07	-3.086
	(5.312)	(5.444)	(-3.692)	(5.28)	(5.45)	(-4.79)
$\alpha$	0.079	0.045		0.076	0.049
	(3.004)	(2.073)		(2.74)	(1.94)
$\alpha^-$		0.058			0.044
		(1.752)			(1.77)
$\beta$	0.914	0.918	0.490	0.917	0.919	0.711
	(44.07)	(38.18)	(3.41)	(41.43)	(36.57)	(10.87)
$\gamma$			0.431			0.388
			(13.95)			(11.25)
$\theta$			-0.171			-0.085
			(-3.65)			(-1.97)
logL	20030.86	20049.18	19713.81	19996.19	20008.22	19827.41