14.1 Nonparametric Regression

In this section we introduce several basic terms and ideas from the theory of nonparametric regressions and explain in particular the method of local polynomial regression. To conclude we explain how this can be applied to (financial) time series. A detailed representation can be found in Härdle et al. (2004).

In nonparametric regression one is interested in the (functional) relationship between an explanatory variable $X$ and a dependent variable $Y$, i.e., one is interested in obtaining an estimation for the unknown function $m(x) = {\mathop{\text{\rm\sf E}}}[Y \, \vert \, X=x]$. In doing this, in contrast to parametric statistics, no special assumptions on the form of the function $m$ is made. Only certain regularity and smoothing assumptions are made about $m$.

One way to estimate $m$ is to use the method of local polynomial regression (LP Method). The idea is based on the fact that the function $m$ can be locally approximated with a Taylor polynomial, i.e., in a neighborhood around a given point $x_0$ it holds that

$$m(x) \approx \sum_{k=0}^p \frac{m^{(k)}(x_0)}{k!}(x-x_0)^k.$$ (14.2)

In order to find an estimate for $m$ at point $x_0$, one therefore tries to find a polynomial based on observations $(X_1, Y_1), \dots, (X_n, Y_n)$ that is a good approximation of $m$ around $x_0$. As a measure of the quality of the approximation one usually chooses a LS criterion, i.e., one wants to minimize the expression

$$\sum_{i=1}^n \Big\{ Y_{i} - \sum_{j=0}^p \beta_j (X_{i} - x_0)^j \Big\}^2$$ (14.3)

with respect to $\beta = (\beta_0,\dots,\beta_p)^\top$. Since the representation  (13.2) holds only locally, one still has to take into consideration that some of the observations $X_i$ may not lie close enough to $x_0$ and thus (13.2) no longer applies to them. One must then sufficiently localize the observations, i.e., only consider those observations that lie close enough to $x_0$.

One of the classical methods for localization is based on weighting the data with the help of a kernel. A kernel is a function $K: \mathbb{R}\longrightarrow [0,\infty)$ with $\int\, K(u)\, du =1$. The most useful kernels are also symmetric and disappear outside of a suitable interval around the zero point.

If $K$ is a kernel and $h > 0$, then the kernel $K_h$

$$K_h (u) = \frac{1}{h} K\big( \frac{u}{h} \big)$$

is re-scaled with the bandwidth $h$, which again integrates to 1. If, for example, the initial kernel $K$ disappears outside of the interval $[-1,1]$, then $K_h$ is zero outside of the interval $[-h,h]$. By weighting the $i-$th term in (13.3) with $K_h (x-X_i)$, one has a minimization problem which, due to the applied localization, can be formulated to be independent of the point $x_0$. The coefficient vector $\hat{\beta} = \hat{\beta}(x) = (\hat{\beta}_0 (x), \dots, \hat{\beta}_p (x))^\top$ that determines the polynomial of the point $x$ is thus given by

$$\hat{\beta} = \arg \min_{\beta} \sum_{i=1}^n \Big\{ Y_{i} - \sum_{j=0}^p \beta_j (x-X_i)^j \Big\}^2 \, K_h(x-X_i).$$ (14.4)

It is obvious that $\hat{\beta}$ depends heavily on the choice of kernel and the bandwidth. Different methods for determining $K$ and $h$ are introduced in Härdle et al. (2004).

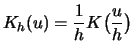
With the representation

$$\mathbf{X} = \left( \begin{array}{ccccc} 1 & X_1-x & (X_1-x)^2 & \dots & (X_1-... ...bf{Y} = \left( \begin{array}{c} Y_1 \\ \vdots \\ Y_n \\ \end{array} \right),$$

$$\mathbf{W} = \left( \begin{array}{ccc} K_h (x-X_1) & & 0 \\ & \ddots & \\ 0 & & K_h(x-X_n) \\ \end{array} \right)$$

the solution $\hat{\beta}$ to the weighted least squares problem (13.4) can be explicitly written as

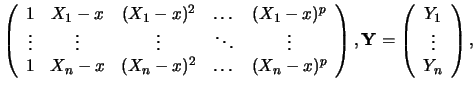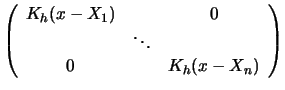$$\hat{\beta}(x) = \big( \mathbf{X}^\top \mathbf{W X} \big)^{-1} \, \mathbf{X}^\top \mathbf{W Y}$$ (14.5)

The estimation $\hat{m}(x)$ for $m(x)$ can be obtained only by calculating the approximating polynomial at $x$:

$$\hat{m}(x) = \hat{\beta}_0 (x).$$ (14.6)

The remaining components of $\hat{\beta}(x)$, due to equations (13.2) and (13.3) deliver estimators for the derivatives of $m$: $\hat{m}^{(j)}(x) = j! \, \hat{\beta}_j (x), j=1, ...,p$, which will not be discussed in further detail here. In the special case where $p=0$, $\hat{m}(x)$ is a typical kernel estimator of Nadaraya-Watson type, see Härdle (1990).

The similarly derived method of local polynomial approximation, or LP method for short, will now be applied to a time series $(Y_i)$. As mentioned before, one is most interested in creating forecasts.

For the simplest case a one-step-ahead forecast means that the functional relationship between $Y_{i-1}$ and a function $\lambda(Y_i)$ of $Y_i$ will be analyzed, i.e., we want to obtain an estimate for the unknown function

$$m(x) = {\mathop{\text{\rm\sf E}}}\big[ \lambda(Y_i)\, \vert\, Y_{i-1} = x \big].$$

In order to apply the LP Method mentioned above, consider a given sample $Y_0, \dots, Y_n$ as observations of the form $(Y_0, Y_1),\dots,(Y_{n-1}, Y_n)$. The process $(Y_i)$ must fulfil certain conditions, so that these observations are identically distributed and in particular so that the function $m$ is independent of the time index $i$. Such is the case when $(Y_i)$ is stationary. By substituting $X_{i} = Y_{i-1}$ into (13.4) and replacing $Y_i$ with $\lambda(Y_i)$, we obtain in this situation

$$\hat{\beta} = \arg \min_{\beta} \sum_{i=1}^n \Big\{\lambda(Y_i) - \sum_{j=0}^p \beta_j (x-Y_{i-1})^j \Big\}^2 \, K_h(x-Y_{i-1}) ,$$ (14.7)

and the estimate for $m(x)$ is again given by $\hat{\beta}_0 (x).$