We consider now an alternative model describing the total claim amount in a fixed period in a portfolio of insurance contracts.
Let ![]() denote the number of claims arising from policies in a given time period. Let
denote the number of claims arising from policies in a given time period. Let ![]() denote the amount of
the first claim,
denote the amount of
the first claim, ![]() the amount of the second claim and so on. In the collective risk model, the random sum
the amount of the second claim and so on. In the collective risk model, the random sum
In Section 18.3.1 we present formulae for the considered premiums in the collective risk model.
In Section 18.3.2 we apply the normal and translated gamma approximations to obtain closed formulae for premiums.
Since for the number of claims ![]() , a Poisson or a negative binomial distribution is often selected, we discuss these cases in detail in Section 18.3.3 and 18.3.4, respectively.
Finally, we illustrate the behavior of the premiums on examples in Section 18.3.5.
, a Poisson or a negative binomial distribution is often selected, we discuss these cases in detail in Section 18.3.3 and 18.3.4, respectively.
Finally, we illustrate the behavior of the premiums on examples in Section 18.3.5.
In order to find formulae for premiums based on the expected value of the total claim, let us assume that
![]() ,
,
![]() ,
,
![]() and
and
![]() exist. For the collective risk model, the expected value of aggregate claims is the product of the expected individual claim amount and the expected number of claims,
exist. For the collective risk model, the expected value of aggregate claims is the product of the expected individual claim amount and the expected number of claims,
Thus it is easy to obtain the following premium formulae in the collective risk model:
| (18.27) |
| (18.28) |
| (18.29) | |||
| (18.30) | |||
If we assume that ![]() and
and ![]() exist, the moment generating function of
exist, the moment generating function of ![]() can be derived as
can be derived as
| (18.31) |
![$\displaystyle P_{E}(c)=\frac{\ln [M_N\{\ln M_X(c)\}]}{c}, \quad c> 0.$](stfhtmlimg2946.gif) |
(18.32) |
It is often difficult to determine the distribution of the aggregate claims and this fact causes problems with calculating the quantile premium given by
| (18.33) |
In Section 18.2.2 the normal approximation was employed as an approximation for the distribution of aggregate claims in the individual risk model. This approach can also be used in the case of the collective model when the expected number of claims is large (Bowers et al.; 1997; Daykin, Pentikainen, and Pesonen; 1994).
The normal approximation simplifies the calculations. If the distribution of ![]() can be approximated by a normal distribution with mean
can be approximated by a normal distribution with mean
![]() and variance
and variance
![]() , the quantile premium is given by the formula
, the quantile premium is given by the formula
Moreover, in the case of the normal approximation, it is possible to express the exponential premium as
| (18.35) |
Let us also mention that since the mean and variance in the case of the normal approximation are the same as for the distribution of ![]() , the premiums based on the expected value are given by the general formulae presented in Section 18.3.1.
, the premiums based on the expected value are given by the general formulae presented in Section 18.3.1.
Unfortunately, the normal approximation is not usually sufficiently accurate. The disadvantage of this approximation lies in the fact that the skewness of the normal distribution is always zero, as it has a symmetric probability density function. Since the distribution of aggregate claims is often skewed, another approximation of the distribution of aggregate claims that accommodates skewness is required. In this section we describe the translated gamma approximation. For more approaches and discussion of their applicability see, for example, Daykin, Pentikainen, and Pesonen (1994).
The distribution function of the translated (shifted) gamma distribution is given by
| (18.36) |
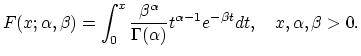 |
(18.37) |
To apply the approximation, the parameters ![]() ,
, ![]() , and
, and ![]() have to be selected so that the first, second, and third central moments of
have to be selected so that the first, second, and third central moments of ![]() equal the corresponding items for the translated gamma distribution. This procedure leads to the following result:
equal the corresponding items for the translated gamma distribution. This procedure leads to the following result:
![$\displaystyle \alpha=4\frac{\{\mathop{\textrm{Var}}(S)\}^3}{(\mathop{\textrm{E}}[\{S-\mathop{\textrm{E}}(S)\}^3])^2},$](stfhtmlimg2952.gif) |
(18.38) |
![$\displaystyle \beta=2\frac{\mathop{\textrm{Var}}(S)}{\mathop{\textrm{E}}[\{S-\mathop{\textrm{E}}(S)\}^3]},$](stfhtmlimg2953.gif) |
(18.39) |
![$\displaystyle x_0=\mathop{\textrm{E}}(S)-2\frac{\{\mathop{\textrm{Var}}(S)\}^2}{\mathop{\textrm{E}}[\{S-\mathop{\textrm{E}}(S)\}^3]}.$](stfhtmlimg2954.gif) |
(18.40) |
In the case of the translated gamma distribution, it is impossible to give a simple analytical formula for the quantile premium. Therefore, in order to find this premium a numerical approximation must be used. However, it is worth noticing that the exponential premium can be presented as
In many applications, the number of claims ![]() is assumed to be described by the Poisson distribution with the probability function given by
is assumed to be described by the Poisson distribution with the probability function given by
The compound Poisson distribution has a number of useful properties. Formulae for the exponential premium and for the premiums based on the expectation of the aggregate claims simplify because
![]() and
and
![]() .
.
Moreover, for large ![]() , the distribution of the compound Poisson can be approximated by a normal distribution with mean
, the distribution of the compound Poisson can be approximated by a normal distribution with mean
![]() and variance
and variance
![]() , and the quantile premium is given by
, and the quantile premium is given by
| (18.43) |
| (18.44) |
If the first three central moments of the individual claim distribution exist, the compound Poisson distribution can be approximated by the translated gamma distribution with the following parameters
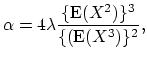 |
(18.45) |
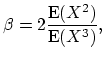 |
(18.46) |
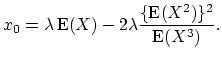 |
(18.47) |
It is worth mentioning that the compound Poisson distribution has many attractive features (Panjer and Willmot; 1992; Bowers et al.; 1997), for example, the combination of a number of portfolios, each of which has a compound Poisson distribution of aggregate claims, also has a compound Poisson distribution of aggregate claims. Moreover, this distribution can be used to approximate the distribution of total claims in the individual model. Although the compound Poisson distribution is normally appropriate in life insurance modeling, it sometimes does not provide an adequate fit to insurance data in other coverages (Willmot; 2001).
When the variance of the number of claims exceeds its mean, the Poisson distribution is not appropriate - in this situation the use of the negative binomial distribution with the probability function given by
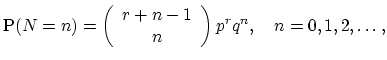 |
(18.48) |
Since for the negative binomial distribution we have
| (18.49) |
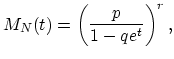 |
(18.50) |
For large ![]() , the distribution of the compound negative binomial can be approximated by a normal distribution with the mean
, the distribution of the compound negative binomial can be approximated by a normal distribution with the mean
![]() and variance
and variance
![]() . In this case the quantile premium is given by
. In this case the quantile premium is given by
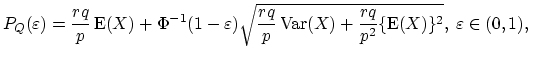 |
(18.51) |
![$\displaystyle P_{E}(c)=\frac{rq}{p}\mathop{\textrm{E}}(X)+\frac{c}{2}\left [\fr...
...\textrm{Var}}(X)+\frac{rq}{p^2}\{\mathop{\textrm{E}}(X)\}^2\right ], \quad c>0.$](stfhtmlimg2975.gif) |
(18.52) |
It is worth mentioning that the negative binomial distribution arises as a mixed Poisson variate. More precisely, various distributions for the number of claims can be generated by assuming that the Poisson parameter ![]() is a random variable with probability distribution function
is a random variable with probability distribution function
![]() ,
, ![]() , and that the conditional distribution of
, and that the conditional distribution of ![]() , given
, given
![]() , is Poisson with parameter
, is Poisson with parameter ![]() . In such case the distribution of
. In such case the distribution of ![]() is called a compound mixed Poisson distribution, see also Chapter 14. This choice might be useful for example when we consider a population of insureds where various classes of insureds within the population generate numbers of claims according to the Poisson distribution, but the Poisson parameters may be different for the various classes. The negative binomial distribution can be derived in this fashion when
is called a compound mixed Poisson distribution, see also Chapter 14. This choice might be useful for example when we consider a population of insureds where various classes of insureds within the population generate numbers of claims according to the Poisson distribution, but the Poisson parameters may be different for the various classes. The negative binomial distribution can be derived in this fashion when
![]() is the gamma probability density function.
is the gamma probability density function.
As the number of policies sold by the insurance company grows, the actuary has decided to try to fit a collective risk model to the
portfolio. The log-normal distribution with the parameters
![]() and
and
![]() (these parameters are again estimated on the base of the real-life data describing losses
resulting from catastrophic events in the USA, see Chapter 13) is chosen to describe the amount of claims. The number of claims is assumed to be Poisson distributed with parameter
(these parameters are again estimated on the base of the real-life data describing losses
resulting from catastrophic events in the USA, see Chapter 13) is chosen to describe the amount of claims. The number of claims is assumed to be Poisson distributed with parameter
![]() . Moreover, the claim amounts and the number of claims are believed to be independent. The actuary wants to compare the behavior of the quantile premium for the whole portfolio of policies given by the general formula (18.34) and in the case of the translated gamma approximation.
. Moreover, the claim amounts and the number of claims are believed to be independent. The actuary wants to compare the behavior of the quantile premium for the whole portfolio of policies given by the general formula (18.34) and in the case of the translated gamma approximation.
Figure 18.3 illustrates how the premium based on the translated gamma approximation (dashed red line) fits the premium determined by the exact compound Poisson distribution (solid blue line). The premium for the original compound distribution has to be determined on the base of numerical simulations. This is the reason why the line is jagged. Better smoothness can be achieved by performing a larger number of Monte Carlo simulations (here we again performed 10000 simulations).
The actuary notices that the approximation fits better for the larger values of
![]() and worse for
its smaller values. In fact the compound distribution functions of the original distribution and its transformed gamma approximation
lay close to each other, but both are increasing and tend to one in infinity. This explains why the quantile premiums - understood as inverse functions of the distribution functions - differ so much for
and worse for
its smaller values. In fact the compound distribution functions of the original distribution and its transformed gamma approximation
lay close to each other, but both are increasing and tend to one in infinity. This explains why the quantile premiums - understood as inverse functions of the distribution functions - differ so much for
![]() close to zero.
close to zero.
The actuary considers again the collective risk model where the number of claims is described by the Poisson distribution with parameter
![]() , i.e. the compound Poisson model. But this time the claims are described by the gamma distribution with the parameters
, i.e. the compound Poisson model. But this time the claims are described by the gamma distribution with the parameters
![]() and
and
![]() (parameters are based on the same catastrophic data as in the previous example).
(parameters are based on the same catastrophic data as in the previous example).
Now the actuary considers the exponential premium for the aggregate claims in this model. The exponential premium in the case of the translated gamma approximation (dashed red line) and the exact premium (solid blue line) are plotted in Figure 18.4. Both premiums - for the original and the approximating distribution - are calculated analytically while it is easy to perform the calculations in this case. Both presented functions increase with the risk aversion parameter. We see that the translated gamma approximation can be a useful and precise tool for calculating the premiums in the collective risk model.