![\includegraphics[width=1\defpicwidth]{_lnsep.ps}](stfhtmlimg1787.gif)
|
Having introduced some elements of statistical learning and demonstrated the potential of SVMs for company rating we can now give a Lagrangian formulation of an SVM for the linear classification problem and generalize this approach to a nonlinear case.
In the linear case the following inequalities hold for all ![]() points of the training set:
points of the training set:
The basic idea of the SVM classification is to find such a separating
hyperplane that corresponds to the largest possible margin between the points
of different classes, see Figure 10.3. Some penalty for
misclassification must also be introduced. The classification error ![]() is
related to the distance from a misclassified point
is
related to the distance from a misclassified point ![]() to the canonical
hyperplane bounding its class. If
to the canonical
hyperplane bounding its class. If ![]() , an error in separating the two
sets occurs. The objective function corresponding to penalized margin
maximization is formulated as:
, an error in separating the two
sets occurs. The objective function corresponding to penalized margin
maximization is formulated as:
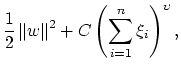 |
(10.11) |
The Lagrange functional for the primal problem for
![]() is:
is:
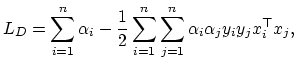 |
(10.13) |
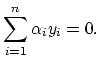 |
Those points ![]() for which the equation
for which the equation
![]() holds
are called support vectors. After training the support vector machine and
deriving Lagrange multipliers (they are equal to 0 for non-support vectors) one
can classify a company described by the vector of parameters
holds
are called support vectors. After training the support vector machine and
deriving Lagrange multipliers (they are equal to 0 for non-support vectors) one
can classify a company described by the vector of parameters ![]() using the
classification rule:
using the
classification rule:
| (10.15) |
The SVMs can also be easily generalized to the nonlinear case. It is worth
noting that all the training vectors appear in the dual Lagrangian formulation
only as scalar products. This means that we can apply kernels to transform all
the data into a high dimensional Hilbert feature space and use linear
algorithms there:
| (10.16) |
If a kernel function ![]() exists such that
exists such that
![]() , then it can be used without knowing the transformation
, then it can be used without knowing the transformation ![]() explicitly. A necessary and sufficient condition for a symmetric function
explicitly. A necessary and sufficient condition for a symmetric function
![]() to be a kernel is given by Mercer's (1909) theorem.
It requires positive definiteness, i.e. for any data set
to be a kernel is given by Mercer's (1909) theorem.
It requires positive definiteness, i.e. for any data set
![]() and any real numbers
and any real numbers
![]() the function
the function ![]() must satisfy
must satisfy
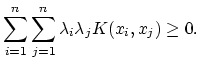 |
(10.17) |