1.2 Quantile Regression Estimation

Some key definitions related to quantile regression are introduced in this section. Besides that, we demonstrate how to use XploRe for the estimation of quantile regression models.

1.2.1 Definitions

Given a random sample ${y}_{1},\ldots,{y}_{n}$, it seems natural to find the approximation of a quantile (e.g., the median $G_Y(1/2)$), in terms of the order statistics $y_{[1]} \leq \ldots \leq y_{[n]}$, i.e., by means of sorting. The crucial point for the concept of quantile regression estimation is that the sample analogue of $Q_Y(\tau)$ can be also found as the argument of the minimum of a specific objective function, because the optimization approach yields a natural generalization of the quantiles to the regression context. The $\tau$-th sample quantile can be found as

$$\mathop{\rm argmin}\limits _{\theta \in \mathbb{R}} \sum_{i = 1}^{n} \rho_{\tau}(y_i - \theta),$$ (1.5)

where

$$\rho_{\tau}(x) = x\cdot\{\tau - I(x < 0)\}$$ (1.6)

(see Figure 1.1) and $I(\cdot)$ represents the indicator function.

Figure 1.1: Quantile regression function $\rho _{\tau }$

Any one-dimensional $M$-statistics (including the least squares estimator and (1.5)) for estimating a parameter of location

$$\hat{\mu} = \mathop{\rm argmin}\limits _{\mu \in \mathbb{R}} \sum_{i = 1}^{n} \psi(y_i - \mu)$$

can be readily extended to the regression context, i.e., to the estimation of conditional expectation function $\mathop{E\hspace{0mm}}\nolimits (Y\vert X=x) = x^T\beta$ by solving

$$\hat{\beta} = \mathop{\rm argmin}\limits _{\beta \in \mathbb{R}^p} \sum_{i = 1}^{n} \psi(y_i - x_i^T\beta),$$

where $y = ({y}_{1},\ldots,{y}_{n})$ is a vector of responses and $X = (x_1,\ldots,x_n)^T$ is an $n \times p$ matrix of explanatory variables. From now on, $n$ will always refer to the number of observations and $p$ to the number of unknown parameters. As the sample quantile estimation is just a special case of $M$-statistics for $\psi = \rho_{\tau}$, it can be adapted for the estimation of the conditional quantile function along the same way. Thus, the unknown parameters in the conditional quantile function $Q_Y(\tau\vert X=x) = x_i^T\beta$ are to be estimated as

$$\hat{\beta}(\tau) = \mathop{\rm argmin}\limits _{\beta \in \mathbb{R}^p} \sum_{i = 1}^{n} \rho_{\tau}(y_i - x_i^T\beta).$$ (1.7)

The special case of $t = 1/2$ is equivalent to minimizing the sum of absolute values of residuals, the well-known $L_1$-estimator.

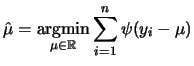
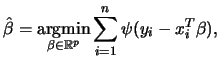
Before proceeding to the description of how such an estimate can be computed in XploRe , two issues have to be discussed. First, given formula (1.7), it is clear that in most cases there exists no general closed-form solution like in the case of the least squares estimator. Therefore, it is natural to ask whether any solution of (1.7) exists at all and whether it is unique. The answer is positive under some rather general conditions. Let $\mathcal{H}_m, m \in \{{1},\ldots,{n}\},$ represent the set of all $m$-element subsets of $\{{1},\ldots,{n}\}$, and let $X_{h}$ denote a $m \times p$ submatrix of $X$ composed from rows ${X}_{h_1,.},\ldots,{X}_{h_m,.}$ for any $m \in \{{1},\ldots,{n}\}$ and $h \in \mathcal{H}_m$. Similarly, let for a vector $y$ be $y_h = ({y}_{h_1},\ldots,{y}_{h_m})^T$. Notice that this convention applies also for $h \in \mathcal{H}_1$, that is, for single numbers. The rows of $X$ taken as column vectors are referred by ${x}_{1},\ldots,{x}_{n}$--therefore, $X = ({x}_{1},\ldots,{x}_{n})^T = (X_1^T,\ldots,X_n^T)^T$. Now we can write Theorem 3.3 of Koenker and Bassett (1978) in the following way:

Let $(y,X)$ be regression observations, $\tau \in (0,1)$. If $(y,X)$ are in general position, i.e., the system of linear equations $y_h = X_h b$ has no solution for any $h \in \mathcal{H}_{p+1}$, then there exists a solution to the quantile regression problem (1.7) of the form $\hat{\beta}(\tau,h) = X_h^{-1} y_h, h \in \mathcal{H}_p,$ if and only if for some $h \in \mathcal{H}_p$ holds

$$(\tau - 1) 1_p \leq \xi_p \leq \tau 1_p,$$ (1.8)

where $\xi_h^T = \sum_{i \not\in h} \rho_{\tau}\{y_i - X_i\hat{\beta}(\tau,h)\} X_i X_h^{-1}$, $\rho _{\tau }$ is defined by (1.6), and $1_p$ is the $p \times 1$ vector of ones. Moreover, $\hat{\beta}(\tau,h)$ is the unique solution if and only if the inequalities are strict, otherwise the solution set is the convex hull of several solutions of the form $\hat{\beta}(\tau,h)$.

The presented result deserves one additional remark. Whereas situations in which observations $(y,X)$ are not in general position are not very frequent unless the response variable is of discrete nature, weak inequality in (1.8), and consequently multiple optimal solutions, can occur when all explanatory variables are discrete.

The second issue we have to mention is related to the numerical computation of estimates. The solution of (1.7) can be found by techniques of the linear programming, because

$$\min_{\beta \in \mathbb{R}^p} \sum_{i = 1}^{n} \rho_{\tau}(y_i - X_i \beta)$$

may be rewritten as the minimization of a linear function subject to linear constraints

$$\min\limits_{\beta \in \mathbb{R}^p; u, v \in \mathbb{R}_+^n} \tau 1_n^T u + (1-\tau) 1_n^T v$$ (1.9)

$$\textrm{subject to} y - X\beta = u - v.$$

The linearity of the objective function and constraints implies that the solution has to lie in one of the vertices of the polyhedron defined by the constraints in (1.9). It is possible to derive that these vertices correspond to elements $h$ of $\mathcal{H}_p$ and take form

$$\hat{\beta}(\tau) = X_h^{-1} y_h$$

$$u = \max\{y - X \hat{\beta}(\tau), 0_n\}, ~\textrm{especially}~u_h = 0$$

$$v = -\min\{y - X \hat{\beta}(\tau), 0_n\}, ~\textrm{especially}~v_h = 0 .$$

Apparently, there are always at least $p$ indices from $\{{1},\ldots,{n}\}$ such that the corresponding residuals are equal to zero. Therefore, traversing between vertices of the polyhedron corresponds to switching between $h_1, h_2 \in \mathcal{H}_p$--hence the method belongs to the group of the so-called exterior-point methods. In order to find the optimal $h$ (or equivalently vertex), we usually employ a modified simplex method (Koenker and D'Orey; 1987). Although this minimization approach has some considerable advantages (for small problems, it is even faster than the least squares computation), it becomes rather slow with an increasing number of observations. Thus, it is not very suitable for large problems ( $n \geq 100000$). Koenker and Portnoy (1997) developed an interior-point method that is rather fast when applied on large data sets.

1.2.2 Computation

z = rqfit (x, y{, tau, ci, alpha, iid, interp, tcrit})

estimates noninteractively a quantile regression model

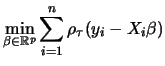
The quantlet of metrics quantlib which serves for the quantile regression estimation is rqfit . We explain just the basic usage of rqfit quantlet in this section, other features will be discussed in the following sections. See Subsection 1.5.1 for detailed description of the quantlet.

The quantlet expects at least two input parameters: an $n \times p$ matrix x that contains $n$ observations of $p$ explanatory variables and an $n \times 1$ vector y of $n$ observed responses. If the intercept is to be included in the regression model, the $n \times 1$ vector of ones can be concatenated to the matrix x in the following way:

  x = matrix(rows(x))~x

Neither the matrix x, nor the vector y should contain missing (NaN) or infinite values (Inf,-Inf). Their presence can be identified by isNaN or isNumber and the invalid observations should be processed before running rqfit , e.g., omitted using paf .

Quantlet rqfit provides a noninteractive way for quantile regression estimation. The basic invocation method is quite simple:

  z = rqfit(x,y,tau)

where parameter tau indicates which conditional quantile function $Q_Y(\tau\vert X)$ has to be estimated. It is even possible to omit it:

  z = rqfit(x,y)

In this case, the predefined value $\tau = 0.5$ is used. The output of rqfit might be little bit too complex, but for now it is sufficient to note that z.coefs refers to the vector of the estimated coefficients $\hat{\beta}(\tau)$ and z.res is the vector of regression residuals. If you want to have also the corresponding confidence intervals, you have to specify extra parameters in the call of rqfit --the fourth one, ci, equal to one, which indicates that you want to get confidence intervals, and optionally the fifth one, alpha, that specifies the nominal coverage probability 1-alpha for the confidence intervals (the default value of alpha is 0.1):

  z = rqfit(x,y,tau,1,alpha)

Then z.intervals gives you the access to the $p \times 2$ matrix of confidence intervals (the first column contains lower bounds, the second one upper bounds). Read Subsection 1.4.3 for more information.

To have a real example, let us use data set nicfoo supplied with XploRe . The data set is two-dimensional, having only one explanatory variable x, a household's net income, in the first column and the response variable y, food expenditures of the household, in the second column. In order to run, for example, the median regression ( $\tau = 0.5$) of y on constant term, x and x$^2$, you have to type at the command line or in the editor window

  data = read("nicfoo")
  x = matrix(rows(data)) ~ data[,1] ~ (data[,1]^2)
  y = data[,2]
  z = rqfit(x,y)
  z.coefs

XAGqr03.xpl

Do not forget to load quantlib metrics before running rqfit :

  library("metrics")

The result of the above example should appear in the XploRe output window as follows:

  Contents of coefs
  [1,]  0.12756
  [2,]   1.1966
  [3,] -0.24616