1.3 Essential Properties of QR

The practical usefulness of any estimation technique is determined, besides other factors, by its invariance and robustness properties, because they are essential for coherent interpretation of regression results. Although some of these properties are often perceived as granted (probably because of their validity in the case of the least squares regression), it does not have to be the case for more evolved regression procedures. Fortunately, quantile regression preserves many of these invariance properties, and even adds to them several other distinctive qualities, which we are going to discuss now.

1.3.1 Equivariance

In many situations it is preferable to adjust the scale of original variables or reparametrize a model so that its result has a more natural interpretation. Such changes should not affect our qualitative and quantitative conclusions based on the regression output. Invariance to a set of some elementary transformations of the model is called equivariance in this context. Koenker and Bassett (1978) formulated four equivariance properties of quantile regression. Once we denote the quantile regression estimate for a given $\tau \in (0,1)$ and observations $(y,X)$ by $\hat{\beta}(\tau;y,X)$, then for any $p \times p$ nonsingular matrix $A, \gamma \in \mathbb{R}^p$, and $a > 0$ holds

1. $\hat{\beta}(\tau;ay,X) = a \hat{\beta}(\tau;y,X)$
2. $\hat{\beta}(\tau;-ay,X) = a \hat{\beta}(1-\tau;y,X)$
3. $\hat{\beta}(\tau;y + X\gamma,X) = \hat{\beta}(\tau;y,X) + \gamma$
4. $\hat{\beta}(\tau;y,XA) = A^{-1} \hat{\beta}(\tau;y,X)$.

This means, for example, that if we use as the measurement unit of $y$ millimeters instead of meters, that is $y$ multiplied by $1000$, then our estimate scales appropriately: $\hat{\beta}(\tau;y[\textrm{mm}],X) = 1000 \cdot \hat{\beta}(\tau;y[\textrm{m}],X)$.

1.3.2 Invariance to Monotonic Transformations

Quantiles exhibit besides ``usual'' equivariance properties also equivariance to monotone transformations. Let $f(\cdot)$ be a nondecreasing function on $\mathbb{R}$--then it immediately follows from the definition of the quantile function that for any random variable $Y$

$$Q_{f(Y)}(\tau) = f\{Q_Y(\tau)\}.$$ (1.10)

In other words, the quantiles of the transformed random variable $f(Y)$ are the transformed quantiles of the original variable $Y$. Please note that this is not the case of the conditional expectation-- $\mathop{E\hspace{0mm}}\nolimits \{f(Y)\} \not= f(EY)$ unless $f(\cdot)$ is a linear function. This is why a careful choice of the transformation of the dependent variable is so important in various econometrics models when the ordinary least squares method is applied (unfortunately, there is usually no guide which one is correct).

We can illustrate the strength of equivariance with respect to monotone transformation on the so-called censoring models. We assume that there exists, for example, a simple linear regression model with i.i.d. errors

$$y_i = x_i^T\beta + \varepsilon _i, ~~~ i \in \{{1},\ldots,{n}\},$$

and that the response variable $y_i$ is unobservable for some reason. Instead, we observe $\tilde{y}_i = \max\{y_i, a\},$ where $a \in \mathbb{R}$ is the censoring point. Because of censoring, the standard least squares method is not consistent anymore (but a properly formulated maximum likelihood estimator can be used). On the contrary, the quantile regression estimator, thanks to the equivariance to monotone transformations, does not run into such problems as noted by Powell (1986). Using $f(x) = \max\{x,a\}$ we can write

$$Q_{\tilde{y}_i}(\tau\vert x_i) = Q_{f(y_i)}(\tau\vert x_i) = f\{Q_{y_i}(\tau\vert x_i)\} = f(x_i^T\beta) = \max\{x_i^T\beta, a\}.$$

Thus, we can simply estimate the unknown parameters by

$$\hat{\beta}(\tau) = \mathop{\rm argmin}\limits _{\beta \in \mathbb{R}^p} \sum_{i = 1}^{n} \rho_{\tau}(y_i - \max\{x_i^T\beta,a\}).$$

1.3.3 Robustness

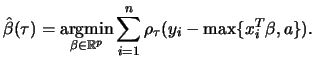
Sensitivity of an estimator to departures from its distributional assumptions is another important issue. The long discussion concerning relative qualities of the mean and median is an example of how significant this kind of robustness (or sensitivity) can be. The sample mean, being a superior estimate of the expectation under the normality of the error distribution, can be adversely affected even by a single observation if it is sufficiently far from the rest of data points. On the other hand, the effect of such a distant observation on the sample median is bounded no matter how far the outlying observation is. This robustness of the median is, of course, outweighed by lower efficiency in some cases. Other quantiles enjoy similar properties--the effect of outlying observations on the $\tau$-th sample quantile is bounded, given that the number of outliers is lower than $n \min\{\tau,1-\tau\}$.

Quantile regression inherits these robustness properties since the minimized objective functions in the case of sample quantiles (1.5) and in the case of quantile regression (1.7) are the same. The only difference is that regression residuals $r_i(\beta) = y_i - x_i^T\beta$ are used instead of deviations from mean $y_i - \mu$. Therefore, quantile regression estimates are reliable in presence of outlying observations that have large residuals. To illustrate this property, let us use a set of ten simulated pseudo-random data points to which one outlying observations is added (the complete code of this example is stored in XAGqr04.xpl ).

  outlier = #(0.9,4.5)     ; outlying observation
;
; data initialization
;
  randomize(17654321)      ; sets random seed
  n = 10                   ; number of observations
  beta = #(1, 2)           ; intercept and slope
  x = matrix(n)~uniform(n) ; randomly generated data
  x = sort(x)
  x = x | (1~outlier[1])   ; add outlier
;
; generate regression line and noisy response variable
;
  regline = x * beta
  y = regline[1:n] + 0.05 * normal(n)
  y = y | outlier[2]       ; add outlier

XAGqr04.xpl

Having the data in hand, we can advance to estimation in the same way as in Subsection 1.2.2. To make results more obvious, they are depicted in a simple graph.

  z = rqfit(x,y,0.5)       ; estimation
  betahat = z.coefs
;
; create graphical display, draw data points and regressions line
;
  d = createdisplay(1,1)
  data = x[,2]~y           ; data points
  outl = outlier[1]~outlier[2] ; outlier
  setmaskp(outl,1,12,15)       ;   is blue big star
;
  line = x[,2]~regline     ; true regression line
  setmaskp(line, 0, 0, 0)
  setmaskl(line, (1:rows(line))', 1, 1, 1)
;
  yhat = x * betahat
  qrline = x[,2]~yhat      ; estimated regression line
  setmaskp(qrline, 0, 0, 0)
  setmaskl(qrline, (1:rows(qrline))', 4, 1, 3)
;
; display all objects
;
  show(d, 1, 1, data[1:n], outl, line, qrline)
  setgopt(d, 1, 1, "title", "Quantile regression with outlier")

XAGqr04.xpl

Figure: Robustness of QR estimates to outliers. XAGqr04.xpl

As a result, you should see a graph like one on Figure 1.2, in which observations are denoted by black circles and the outlier is represented by the big blue star in the right upper corner of the graph. Further, the blue line depicts the true regression line, while the thick red line shows the estimated regression line.

As you may have noticed, we mentioned the robustness of quantile regression with respect to observations that are far in the direction of the dependent variable, i.e., that have large residuals. Unfortunately, this cannot be said about the effect of observations that are distant in the space of explanatory variables--a single point dragged far enough toward infinity can cause that all quantile regression hyperplanes go through it. As an example, let us consider the previous data set with a different outlier:

  outlier = #(3,2)

Running example XAGqr05.xpl with this leverage point gives dramatically different results than in the previous case, see Figure 1.3.

Figure: Nonrobustness of QR estimates to leverage points. XAGqr05.xpl