2.2 Classical Assumptions of the MLRM
In order
to carry out the estimation and inference in the MLRM, the
specification of this model includes a set of assumptions
referring to the way of generating the data, that is to say,
referring to the underlying Data Generating Process (DGP). These
assumptions can be grouped into two categories:
- Hypotheses on the systematic part of the model: strict
exogeneity of the explanatory variables, full rank for the
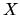 matrix, and stability of the parameter vector
matrix, and stability of the parameter vector 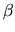 .
.
- Hypotheses on the disturbances of the model: zero
mean, constant variance, non autocorrelation, and normal
distribution function.
2.2.1 The Systematic Component Assumptions
In Economics, it is very difficult to have experimental data
(obtained from a controlled experiment), so it seems reasonable to
assume that the set of variables included in the model should be
random variables. Following Engle, Hendry, and Richard (1983), we can
say that the regressors are
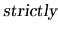
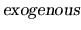 if
if 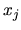 is independent of
is independent of 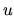 ,
, 
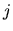 . This means that, given the DGP, for each observed sample
(realization) of every variable included in
. This means that, given the DGP, for each observed sample
(realization) of every variable included in 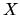 , there are
infinite possible realizations of
, there are
infinite possible realizations of 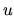 and
and 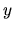 ; this fact leads us
to deal with the distribution of
; this fact leads us
to deal with the distribution of 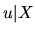 . This assumption allows us
to express the joint distribution function of
. This assumption allows us
to express the joint distribution function of 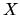 and
and 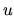 as :
as :
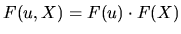 |
(2.4) |
or alternatively:
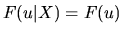 |
(2.5) |
Nevertheless, in this chapter we are going to adopt a more
restrictive assumption, considering the variables in 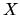 as non
stochastic, that is to say, the elements in
as non
stochastic, that is to say, the elements in 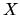 are fixed for
repeated samples. Obviously, this hypothesis allows us to maintain
result (2.5). Thus, we can conclude that the randomness
of
are fixed for
repeated samples. Obviously, this hypothesis allows us to maintain
result (2.5). Thus, we can conclude that the randomness
of 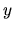 is only due to the disturbance term.
is only due to the disturbance term.
Additionally, the X matrix satisfies the following condition:
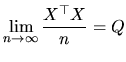 |
(2.6) |
where 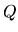 is a non singular positive definite matrix with finite
elements.
is a non singular positive definite matrix with finite
elements.
Analytically, this assumption is written:
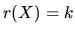 |
(2.7) |
and it means that the columns of X are linearly independent, or in
other words, no exact linear relations exist between any of the
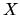 variables. This assumption is usually denoted
variables. This assumption is usually denoted
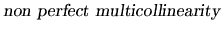 . A direct consequence of
(2.7) is that
. A direct consequence of
(2.7) is that 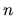
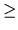
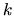 .
.
This assumption means that the coefficients of the model do not
vary across sample observations, that is to say, we assume the
same model for all the sample.
2.2.2 The Random Component Assumptions
Analytically, we write this as:
 |
(2.8) |
or in matrix notation:
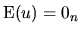 |
(2.9) |
Since 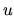 is usually considered as the sum of many individual
factors whose sign is unknown, we assume that on average, these
effects are null.
is usually considered as the sum of many individual
factors whose sign is unknown, we assume that on average, these
effects are null.
This assumption states that the disturbances have constant
variance, and they are non correlated.
 |
(2.10) |
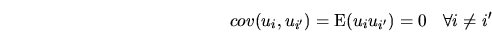 |
(2.11) |
The condition (2.10) is known as
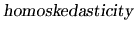 , and it states that all
, and it states that all 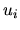 have
the same dispersion around their mean, whatever the values of the
regressors. The condition (2.11), related to the
covariance of the disturbances, is called
have
the same dispersion around their mean, whatever the values of the
regressors. The condition (2.11), related to the
covariance of the disturbances, is called
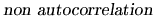 , and it means that knowing the
, and it means that knowing the 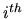 disturbance does not tell us anything about the
disturbance does not tell us anything about the 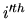 disturbance, for
disturbance, for 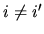 . Both hypotheses can be summarized in
matrix form through the variance-covariance matrix
. Both hypotheses can be summarized in
matrix form through the variance-covariance matrix 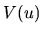 :
:
![$\displaystyle V(u)=\textrm{E}[(u-\textrm{E}u)(u-\textrm{E} u)^{\top }]=\textrm{E}(uu^{\top })=\sigma^{2}I_{n}$](xegbohtmlimg440.gif) |
(2.12) |
This hypothesis, together with (2.9) and (2.12)
allows us to summarize the assumptions of the disturbance term as
follows:
![$\displaystyle u \sim N[0_{n},\sigma^{2}I_{n}]$](xegbohtmlimg441.gif) |
(2.13) |
From (2.13) we derive that all observations of 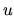 are
independent.
are
independent.
We can find some text books (Baltagi (1999),
Davidson (2000), Hayashi (2000),
Intriligator, Bodkin, and Hsiao (1996), Judge, Carter, Griffiths, Lutkepohl and Lee (1988))
which do not initially include this last assumption in their set
of classical hypotheses, but it is included later. This fact can
be justified because it is possible to get the estimate of the
parameters of the model by the Least Square method, and derive
some of their properties, without using the normality assumption.
From (2.13), the joint density function of the 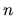 disturbances is given by:
disturbances is given by:
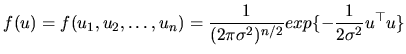 |
(2.14) |
The set of classical assumptions described above allows us to
obtain the probability distribution of the endogenous variable
(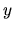 ) as a multivariate normal distribution, with the following
moments:
) as a multivariate normal distribution, with the following
moments:
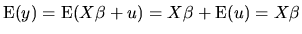 |
(2.15) |
![$\displaystyle V(y)=\textrm{E}[(y-\textrm{E}y)(y-\textrm{E} y)^{\top }]=\textrm{E}(uu^{\top })=\sigma^{2}I_{n}$](xegbohtmlimg444.gif) |
(2.16) |
These results imply that, the expectation for every component of
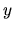 , depends on the corresponding row of
, depends on the corresponding row of 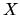 , while all elements
have the same variance, and are independent.
, while all elements
have the same variance, and are independent.
Obviously, we can not assure that the set of classical assumptions
that we have previously described are always maintained. In
practice, there are many situations for which the theoretical
model which establishes the relationship among the set variables
does not satisfy the classical hypotheses mentioned above. A
later section of this chapter and the following chapters of this
book study the consequences when some of the "ideal conditions"
fails, and describe how to proceed in this case. Specifically, at
the end of this chapter we deal with the non stability of the
coefficient vector 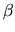 .
.
![]() as non
stochastic, that is to say, the elements in
as non
stochastic, that is to say, the elements in ![]() are fixed for
repeated samples. Obviously, this hypothesis allows us to maintain
result (2.5). Thus, we can conclude that the randomness
of
are fixed for
repeated samples. Obviously, this hypothesis allows us to maintain
result (2.5). Thus, we can conclude that the randomness
of ![]() is only due to the disturbance term.
is only due to the disturbance term.
![]() disturbances is given by:
disturbances is given by:
![]() ) as a multivariate normal distribution, with the following
moments:
) as a multivariate normal distribution, with the following
moments:
![]() , depends on the corresponding row of
, depends on the corresponding row of ![]() , while all elements
have the same variance, and are independent.
, while all elements
have the same variance, and are independent.
![]() .
.