2.8 Restricted and Unrestricted Regression
In
previous sections we made use of the LS and ML principles to
derive estimators of the unknown parameters of the MLRM. In using
these principles, we assumed that our information level was only
the sample information, so it was considered there was no a priori
information on the parameters of the model. However, in some
situations it is possible to have some non-sample information (a
priori information on the parameters), which can be of several
kinds. Now we focus only on exact a priori information about
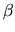 coefficients (useful references for this topic are
Fomby, Carter, and Johnson (1984) and
Judge, Griffiths, Carter, Lutkepohl and Lee (1985)).
coefficients (useful references for this topic are
Fomby, Carter, and Johnson (1984) and
Judge, Griffiths, Carter, Lutkepohl and Lee (1985)).
In general, this previous information on the coefficients can be
expressed as follows:
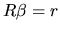 |
(2.153) |
where 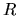 and
and 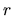 are the matrix and the vector which was defined
to establish the test given in (2.134). Now
(2.153) can be thought of as the way of expressing
the a priori information about the elements of the
are the matrix and the vector which was defined
to establish the test given in (2.134). Now
(2.153) can be thought of as the way of expressing
the a priori information about the elements of the 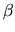 vector.
vector.
In this section, our objective consists of estimating the
parameters of the MLRM by considering the a priori information.
Basically, there are two equivalent ways of carrying out such an
estimation. One of them consists of incorporating the a priori
information into the specified model, in such a way that a
transformed model is obtained whose unknown parameters are
estimated by OLS or ML. The other way of operating consists of
applying either what we call the restricted least squares (RLS)
method, or what we call the restricted maximum likelihood (RML)
method.
2.8.1 Restricted Least Squares and Restricted Maximum Likelihood Estimators
Given the MLRM
and the a priori information about 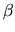 expressed as
expressed as
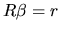 , we try to find the vector
, we try to find the vector
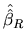 which minimizes the squared sum of residuals (if we use the LS
method) or maximizes the likelihood function (in the case of the
ML method), subject to
which minimizes the squared sum of residuals (if we use the LS
method) or maximizes the likelihood function (in the case of the
ML method), subject to
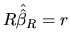 . Then, the
estimator which we obtain by combining all the information is
called
. Then, the
estimator which we obtain by combining all the information is
called
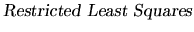 or
or
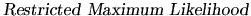 , respectively.
, respectively.
The conditioned optimization problem can be solved through the
classical Lagrangian procedures. If we first consider the LS
method, the corresponding Lagrange function is:
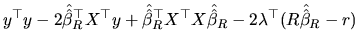 |
(2.154) |
where 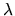 is the
is the
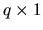 vector of Lagrange
multipliers. The 2 in the last term appears to make the derivation
easier and does not affect the outcome.
vector of Lagrange
multipliers. The 2 in the last term appears to make the derivation
easier and does not affect the outcome.
To determine the optimum values, we set the partial derivatives of
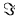 with respect to
with respect to 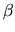 and
and 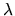 equal to zero:
equal to zero:
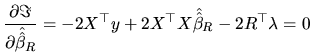 |
(2.155) |
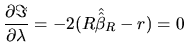 |
(2.156) |
We substitute
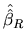 by
by
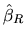 in
order to obtain the value of
in
order to obtain the value of
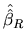 which
satisfies the first-order conditions. Then, from
(2.155) we have:
which
satisfies the first-order conditions. Then, from
(2.155) we have:
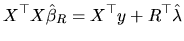 |
(2.157) |
In premultiplying the last expression by
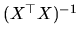 we
get:
we
get:
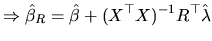 |
(2.158) |
where
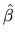 is the unrestricted least squares estimator
which was obtained in (2.25).
is the unrestricted least squares estimator
which was obtained in (2.25).
Expression (2.158) is premultiplied by 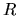 and we get:
and we get:
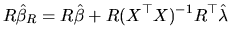 |
(2.159) |
Since
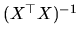 is a positive definite matrix,
is a positive definite matrix,
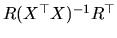 is also positive definite, and
moreover, its rank is
is also positive definite, and
moreover, its rank is 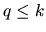 and it is nonsingular. Then, from
(2.159) we may obtain:
and it is nonsingular. Then, from
(2.159) we may obtain:
or
![$\displaystyle \hat{\lambda}=[R(X^{\top }X)^{-1}R^{\top }]^{-1}(r-R\hat{\beta})$](xegbohtmlimg827.gif) |
(2.160) |
because from (2.156), the restricted
minimization problem must satisfy the side condition
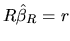 . Using the value (2.160) for
the vector
. Using the value (2.160) for
the vector 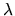 , we get from (2.158) the estimator:
, we get from (2.158) the estimator:
![$\displaystyle \hat{\beta}_{R}=\hat{\beta}+(X^{\top }X)^{-1}R^{\top }[R(X^{\top }X)^{-1}R^{\top }]^{-1}(r-R\hat{\beta})$](xegbohtmlimg829.gif) |
(2.161) |
which is denoted as the restricted least squares (RLS) estimator.
Given that
![$ (X^{\top }X)^{-1}R^{\top }[R(X^{\top }X)^{-1}R^{\top }]^{-1}$](xegbohtmlimg830.gif) is a matrix of constant elements, from (2.161) we can
see that the difference between
is a matrix of constant elements, from (2.161) we can
see that the difference between
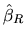 and
and
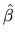 is a linear function of the
is a linear function of the
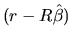 vector. Moreover, we deduce that this difference increases the
further
vector. Moreover, we deduce that this difference increases the
further
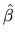 (unrestricted LS) is from satisfying the
restriction.
(unrestricted LS) is from satisfying the
restriction.
According to the RLS estimator, the residuals vector can be
defined as:
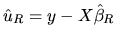 |
(2.162) |
and, analogously to the procedure followed to obtain
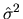 , the RLS estimator of
, the RLS estimator of
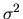 is given by:
is given by:
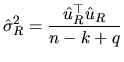 |
(2.163) |
which is an unbiased estimator of
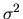 , given that
, given that
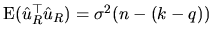 .
.
Having obtained the expressions of the RLS estimators of the
parameters in the MLRM, we now have the required information in
order to prove the equivalence between (2.139) and
(2.140), established in the previous section. In order
to show such equivalence, we begin by adding and subtracting
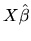 to and from (2.162):
to and from (2.162):
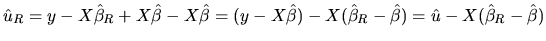 |
(2.164) |
and then, given that
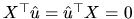 (an
algebraic property of the LS method, described in the estimation
section), we have:
(an
algebraic property of the LS method, described in the estimation
section), we have:
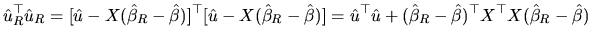 |
(2.165) |
From (2.165), we can write:
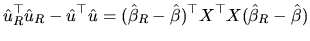 |
(2.166) |
and if we substitute
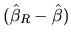 according to
(2.161), we have
according to
(2.161), we have
![$\displaystyle \hat{u}_{R}^{\top }\hat{u}_{R}-\hat{u}^{\top }\hat{u}=(r-R\hat{\beta})^{\top }[R(X^{\top }X)^{-1}R^{\top }]^{-1}(r-R\hat{\beta})$](xegbohtmlimg841.gif) |
(2.167) |
This last expression allows us to conclude that (2.139)
and (2.140) are equivalent. Additionally, from
(2.167) it is satisfied that
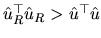 , given
that
, given
that
![$ [R(X^{\top }X)^{-1}R^{\top }]^{-1}$](xegbohtmlimg843.gif) is a positive definite
matrix.
is a positive definite
matrix.
In order to derive now the RML estimators, the Lagrange function
according to the ML principle is written as:
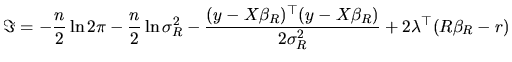 |
(2.168) |
and the first-order conditions are:
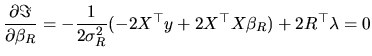 |
(2.169) |
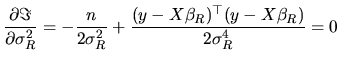 |
(2.170) |
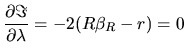 |
(2.171) |
From (2.169)-(2.171), and putting 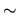 to the parameters, in a similar way to the RLS procedure, we
deduce:
to the parameters, in a similar way to the RLS procedure, we
deduce:
![$\displaystyle \tilde{\beta}_{R}= \tilde{\beta}+(X^{\top }X)^{-1}R^{\top }[R(X^{\top }X)^{-1}R^{\top }]^{-1}(r-R\tilde{\beta})$](xegbohtmlimg849.gif) |
(2.172) |
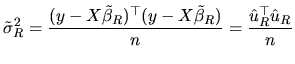 |
(2.173) |
![$\displaystyle \tilde{\lambda}=\frac{[R(X^{\top }X)^{-1}R^{\top }]^{-1}(r-R\tilde{\beta})}{\tilde{\sigma}^{2}_{R}}$](xegbohtmlimg851.gif) |
(2.174) |
so we conclude that, in a MLRM which satisfies the classical
assumptions, the RLS estimators of the coefficients are the same
as the RML estimators. This allows us to write the equality given
in (2.173).
2.8.2 Finite Sample Properties of the Restricted Estimator Vector
Given the equality between
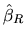 and
and
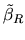 , the following proofs are valid for both
procedures.
, the following proofs are valid for both
procedures.
Before deriving some properties, it is convenient to obtain the
expectation vector and the variance-covariance matrix of the
restricted estimator vector. Using (2.161), the
expected value of
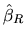 is :
is :
![$\displaystyle \beta+(X^{\top }X)^{-1}R^{\top }[R(X^{\top }X)^{-1}R^{\top }]^{-1}(r-R\beta)$](xegbohtmlimg854.gif) |
(2.175) |
and the variance-covariance matrix:
If we consider expression (2.54) and it is substituted
into (2.161), we can write:
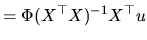 |
(2.176) |
The 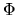 matrix (which premultiplies to
matrix (which premultiplies to
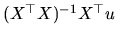 in (2.176), is a
in (2.176), is a
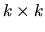 idempotent matrix of constant elements. From this last
expression we obtain:
idempotent matrix of constant elements. From this last
expression we obtain:
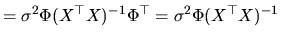 |
(2.177) |
The last equality of (2.177) is written according to
the proof presented in Judge, Carter, Griffiths, Lutkepohl and Lee (1988)
From (2.177), it is possible to deduce the
relationship between
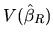 and
and
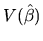 , by
replacing
, by
replacing 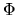 by its expression, and thus:
by its expression, and thus:
with C being a positive semidefinite matrix, as
Fomby, Carter, and Johnson (1984) show. Consequently, the diagonal
elements of
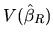 (variances of each
(variances of each
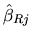 ) are equal to or less than the corresponding
elements of
) are equal to or less than the corresponding
elements of
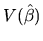 (variances of each
(variances of each
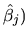 . This means that, if the a priori information
is correct (as we will show later , in this case
. This means that, if the a priori information
is correct (as we will show later , in this case
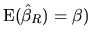 , the estimator vector
, the estimator vector
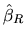 is more efficient than the OLS estimator.
is more efficient than the OLS estimator.
On the basis of these previous results, we can establish the
finite properties of the RLS estimator.
- Linearity. If we substitute expression (2.54)
of
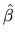 into (2.161), and then we group terms,
we obtain:
into (2.161), and then we group terms,
we obtain:
![$\displaystyle \hat{\beta}_{R}=(X^{\top }X)^{-1}R^{\top }[R(X^{\top }X)^{-1}R^{\top }]^{-1}r+$](xegbohtmlimg870.gif) |
(2.178) |
Given that the first term of the right-hand side of
(2.178) is a vector of constant elements, and the
second term is the product of a matrix of constant elements
multiplied by the vector 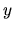 , it follows that
, it follows that
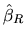 satisfies the linearity property.
satisfies the linearity property.
- Unbiasedness. According to (2.175),
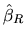 is unbiased only if
is unbiased only if
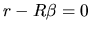 , that is to
say, if the a priori information is true.
, that is to
say, if the a priori information is true.
- BLUE. With correct a priori information, the estimator
vector
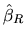 is the best linear unbiased vector within
the class of unbiased estimators that are linear functions of the
endogenous variable and that also satisfy the a priori information
(2.153). This property, which we will not prove
here, is based on the Gauss-Markov Theorem.
is the best linear unbiased vector within
the class of unbiased estimators that are linear functions of the
endogenous variable and that also satisfy the a priori information
(2.153). This property, which we will not prove
here, is based on the Gauss-Markov Theorem.
- Efficiency. As Rothemberg (1973) shows, when the a
priori information is correct, the estimator vector
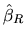 satisfies the Cramer-Rao inequality, and
consequently, it is efficient.
satisfies the Cramer-Rao inequality, and
consequently, it is efficient.
From (2.177) it can be deduced that the expression of
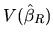 does not change if the a priori information
is correct or non correct, which means that
does not change if the a priori information
is correct or non correct, which means that
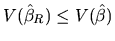 is maintained whatever the situation.
is maintained whatever the situation.
Finally, given the linearity of
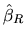 with respect to
with respect to
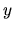 , and this vector being normally distributed, if the a priori
information is correct, we have:
, and this vector being normally distributed, if the a priori
information is correct, we have:
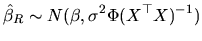 |
(2.179) |
2.8.3 Example
We now consider that we have
the following a priori information on the coefficients:
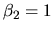 , in such a way that we calculate the restricted
estimators of the coefficients. Jointly with these estimators the
quantlet XEGmlrm06.xpl computes the F statistic as a
function of the restricted and unrestricted squared sum of the
residuals which allows us to test
, in such a way that we calculate the restricted
estimators of the coefficients. Jointly with these estimators the
quantlet XEGmlrm06.xpl computes the F statistic as a
function of the restricted and unrestricted squared sum of the
residuals which allows us to test
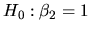 .
.
Note that the RML estimator satisfies the formulated restriction,
and the value of the F statistic is the same as the one obtained
in Section 2.7.4
![]() coefficients (useful references for this topic are
Fomby, Carter, and Johnson (1984) and
Judge, Griffiths, Carter, Lutkepohl and Lee (1985)).
coefficients (useful references for this topic are
Fomby, Carter, and Johnson (1984) and
Judge, Griffiths, Carter, Lutkepohl and Lee (1985)).
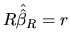 . Then, the
estimator which we obtain by combining all the information is
called
. Then, the
estimator which we obtain by combining all the information is
called
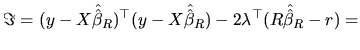
![]() with respect to
with respect to ![]() and
and ![]() equal to zero:
equal to zero:
![]() and we get:
and we get:
![]() is a positive definite matrix,
is a positive definite matrix,
![]() is also positive definite, and
moreover, its rank is
is also positive definite, and
moreover, its rank is ![]() and it is nonsingular. Then, from
(2.159) we may obtain:
and it is nonsingular. Then, from
(2.159) we may obtain:
![]() is a matrix of constant elements, from (2.161) we can
see that the difference between
is a matrix of constant elements, from (2.161) we can
see that the difference between
![]() and
and
![]() is a linear function of the
is a linear function of the
![]() vector. Moreover, we deduce that this difference increases the
further
vector. Moreover, we deduce that this difference increases the
further
![]() (unrestricted LS) is from satisfying the
restriction.
(unrestricted LS) is from satisfying the
restriction.
![]() to and from (2.162):
to and from (2.162):
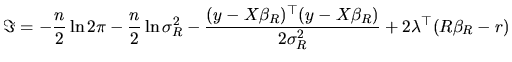
![]() is :
is :
![]() matrix (which premultiplies to
matrix (which premultiplies to
![]() in (2.176), is a
in (2.176), is a
![]() idempotent matrix of constant elements. From this last
expression we obtain:
idempotent matrix of constant elements. From this last
expression we obtain:
![]() and
and
![]() , by
replacing
, by
replacing ![]() by its expression, and thus:
by its expression, and thus:
![]() with respect to
with respect to
![]() , and this vector being normally distributed, if the a priori
information is correct, we have:
, and this vector being normally distributed, if the a priori
information is correct, we have: