We have determined the population properties of the wide class of
![]() models but, in practice, we have a time series and we want
to infer which
models but, in practice, we have a time series and we want
to infer which ![]() model can have generated this time series.
The selection of the appropriate
model can have generated this time series.
The selection of the appropriate ![]() model for the data is
achieved by a iterative procedure based on three steps
(Box, Jenkins and Reinsel; 1994):
model for the data is
achieved by a iterative procedure based on three steps
(Box, Jenkins and Reinsel; 1994):
In this section we will explain this procedure in detail illustrating each step with an example.
Since a stationary ![]() process is characterized in terms of the
moments of the distribution, meanly its mean, ACF and PACF, it is
necessary to estimate them using the available data in order to
make inference about the underlying process.
process is characterized in terms of the
moments of the distribution, meanly its mean, ACF and PACF, it is
necessary to estimate them using the available data in order to
make inference about the underlying process.
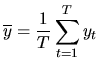 |
(4.39) |
Sometimes it is useful to check whether the mean of a process is zero or
not, that is, to test
![]() against
against
![]() . Under
. Under ![]() the test statistic
the test statistic
![]() follows approximately a normal distribution.
follows approximately a normal distribution.
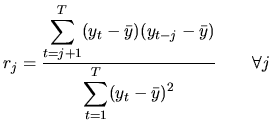
In order to identify the underlying process, it is useful to check
whether these coefficients are statistically nonzero or, more
specifically, to check whether ![]() is a white noise. Under the
assumption that
is a white noise. Under the
assumption that
![]() , the distribution of
these coefficients in large samples can be approximated by:
, the distribution of
these coefficients in large samples can be approximated by:
Then a usual test of individual significance can be applied, i.e.,
![]() against
against
![]() for any
for any
![]() . The null hypothesis
. The null hypothesis ![]() would be rejected
at the 5% level of significance if:
would be rejected
at the 5% level of significance if:
Usually, the correlogram plots the ACF jointly with these two-standard
error bands around zero, approximated by
![]() , that allow
us to carry out this significance test by means of an easy graphic method.
, that allow
us to carry out this significance test by means of an easy graphic method.
We are also interested in whether a set of ![]() autocorrelations are jointly zero or not, that is, in testing
autocorrelations are jointly zero or not, that is, in testing
![]() . The most usual
test statistic is the Ljung-Box statistic:
. The most usual
test statistic is the Ljung-Box statistic:
Under the assumption that
![]() , the
distribution of the sample coefficients
, the
distribution of the sample coefficients
![]() in large
samples is identical to those of the sample ACF (4.40).
In consequence, the rule for rejecting the null hypothesis of
individual non-significance (4.41) is also applied to the
PACF. The bar plot of the sample PACF is called the sample partial
correlogram and usually includes the two standard error bands
in large
samples is identical to those of the sample ACF (4.40).
In consequence, the rule for rejecting the null hypothesis of
individual non-significance (4.41) is also applied to the
PACF. The bar plot of the sample PACF is called the sample partial
correlogram and usually includes the two standard error bands
![]() to assess for individual significance.
to assess for individual significance.
The objective of the identification is to select a subclass of the
family of ![]() models appropriated to represent a time series.
We follow a two step procedure: first, we get a stationary time
series, i.e., we select the parameter
models appropriated to represent a time series.
We follow a two step procedure: first, we get a stationary time
series, i.e., we select the parameter ![]() of the
Box-Cox transformation and the order of integration
of the
Box-Cox transformation and the order of integration ![]() , and
secondly we identify a set of stationary
, and
secondly we identify a set of stationary ![]() processes to
represent the stationary process, i.e. we choose the orders
processes to
represent the stationary process, i.e. we choose the orders
![]() .
.
Our task is to identify if the time series could have been
generated by a stationary process. First, we use the timeplot of
the series to analyze if it is variance stationary. The
series departs from this property when the dispersion of the data
varies along time. In this case, the stationarity in variance is
achieved by applying the appropriate Box-Cox
transformation (4.17) and as a result, we get the series
![]() .
.
The second part is the analysis of the stationarity in mean.
The instruments are the timeplot, the sample
correlograms and the tests for unit roots and stationarity. The
path of a nonstationary series usually shows an upward or downward
slope or jumps in the level whereas a stationary
series moves around a unique level along time. The sample
autocorrelations of stationary processes are consistent estimates
of the corresponding population coefficients, so the sample
correlograms of stationary processes go to zero for moderate lags.
This type of reasoning does not follow for
nonstationary processes because their theoretical autocorrelations
are not well defined. But we can argue that a 'non-decaying'
behavior of the sample ACF should be due to a lack of
stationarity. Moreover, typical profiles of sample
correlograms of integrated series are shown in
figure 4.14: the sample ACF tends to damp very slowly
and the sample PACF decays very quickly, at lag ![]() , with the
first value close to unity.
, with the
first value close to unity.
When the series shows nonstationary patterns, we should take first
differences and analyze if
![]() is stationary
or not in a similar way. This process of taking successive
differences will continue until a stationary time series is
achieved. The graphics methods can be supported with the
unit-root and stationarity tests developed in
subsection 4.3.3. As a result, we have a stationary time
series
is stationary
or not in a similar way. This process of taking successive
differences will continue until a stationary time series is
achieved. The graphics methods can be supported with the
unit-root and stationarity tests developed in
subsection 4.3.3. As a result, we have a stationary time
series
![]() and the order of
integration
and the order of
integration ![]() will be the number of times that we have
differenced the series
will be the number of times that we have
differenced the series
![]() .
.
|
The mean of the process is closely connected with the parameter
![]() : when the constant term is zero, the process has zero
mean (see equation (4.22)). Then a constant term will be
added to the model if
: when the constant term is zero, the process has zero
mean (see equation (4.22)). Then a constant term will be
added to the model if
![]() is rejected.
is rejected.
The orders ![]() are selected comparing the sample ACF and PACF of
are selected comparing the sample ACF and PACF of ![]() with the theoretical patterns of
with the theoretical patterns of ![]() processes that are summarized in
table 4.1.
processes that are summarized in
table 4.1.
Figure 4.15 plots the time series ![]() . It
suggests that the variance could be changing. The plot of the
. It
suggests that the variance could be changing. The plot of the
![]() shows a more stable pattern in variance, so we select
the transformation parameter
shows a more stable pattern in variance, so we select
the transformation parameter ![]() . This series
. This series
![]() appears to be stationary since it evolves around a constant level
and the correlograms decay quickly (see
figure 4.16). Furthermore the ADF test-value is
appears to be stationary since it evolves around a constant level
and the correlograms decay quickly (see
figure 4.16). Furthermore the ADF test-value is
![]() , that clearly rejects the unit-root hypothesis. Therefore,
the stationary time series we are going to analyze is
, that clearly rejects the unit-root hypothesis. Therefore,
the stationary time series we are going to analyze is
![]() .
.
As far as the selection of the orders ![]() is concerned, we
study the correlograms of figure 4.16 and the
numerical values of the first five coefficients that are reported
in table 4.2. The main feature of the ACF is its
damping sine-cosine wave structure that reflects the behavior of
an
is concerned, we
study the correlograms of figure 4.16 and the
numerical values of the first five coefficients that are reported
in table 4.2. The main feature of the ACF is its
damping sine-cosine wave structure that reflects the behavior of
an ![]() process with complex roots. The PACF, where the
process with complex roots. The PACF, where the
![]() is rejected only for
is rejected only for ![]() , leads us to
select the values
, leads us to
select the values ![]() for the
for the ![]() model.
model.
The statistic for testing the null hypothesis
![]() takes the value 221.02. Given a significance level of 5%, we
reject the null hypothesis of zero mean and a constant should be
included into the model. As a result, we propose an
takes the value 221.02. Given a significance level of 5%, we
reject the null hypothesis of zero mean and a constant should be
included into the model. As a result, we propose an
![]() model for
model for
![]() :
:
The parameters of the selected
![]() model can be estimated
consistently by least-squares or by maximum likelihood. Both estimation
procedures are based on the computation of the innovations
model can be estimated
consistently by least-squares or by maximum likelihood. Both estimation
procedures are based on the computation of the innovations
![]() from the values of the stationary variable. The least-squares methods
minimize the sum of squares,
from the values of the stationary variable. The least-squares methods
minimize the sum of squares,
The log-likelihood can be derived from the joint probability density
function of the innovations
![]() , that
takes the following form under the normality assumption,
, that
takes the following form under the normality assumption,
![]() :
:
In order to solve the estimation problem, equations (4.43) and
(4.44) should be written in terms of the observed data and the set of
parameters
![]() . An
. An ![]() process for the
stationary transformation
process for the
stationary transformation ![]() can be expressed as:
can be expressed as:
Then, to compute the innovations corresponding to a given set of
observations
![]() and parameters, it is necessary to count
with the starting values
and parameters, it is necessary to count
with the starting values
![]() ,
,
![]() . More realistically, the innovations should be
approximated by setting appropriate conditions about the initial values,
giving to conditional least squares or conditional maximum
likelihood estimators. One procedure consists of setting the initial values
equal to their unconditional expectations, that is,
. More realistically, the innovations should be
approximated by setting appropriate conditions about the initial values,
giving to conditional least squares or conditional maximum
likelihood estimators. One procedure consists of setting the initial values
equal to their unconditional expectations, that is,
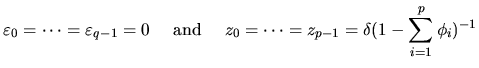
A second useful mechanism is to assume that the first ![]() observations of
observations of
![]() are the starting values and the previous innovations are again equal to
zero. In this case we run the equation (4.45) from
are the starting values and the previous innovations are again equal to
zero. In this case we run the equation (4.45) from ![]() onwards.
For example, for an
onwards.
For example, for an ![]() process, it is
process, it is
Least squares estimation conditioned on the first ![]() observations become
straightforward in the case of pure
observations become
straightforward in the case of pure ![]() models, leading to linear Least
Squares. For example, for the
models, leading to linear Least
Squares. For example, for the ![]() process with zero mean, and
conditioned on the first value
process with zero mean, and
conditioned on the first value ![]() , equation (4.43) becomes the linear
problem,
, equation (4.43) becomes the linear
problem,
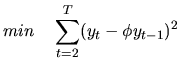
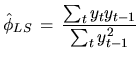
In a general model with a ![]() component the optimization problem
(4.43) is nonlinear. For example, to estimate the parameter
component the optimization problem
(4.43) is nonlinear. For example, to estimate the parameter ![]() of the
of the ![]() process, we substitute equation (4.46) in
(4.43),
process, we substitute equation (4.46) in
(4.43),
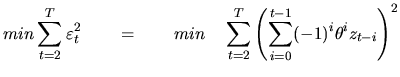
The maximization of this function gives the LS
estimator. Instead of setting the initial conditions, we can compute
the unconditional likelihood. For an ![]() model, the joint density
function can be decomposed as:
model, the joint density
function can be decomposed as:
where the marginal distribution of ![]() is normal with zero mean,
if
is normal with zero mean,
if ![]() , and variance
, and variance
![]() .
Then, the exact log-likelihood under the normality assumption is:
.
Then, the exact log-likelihood under the normality assumption is:
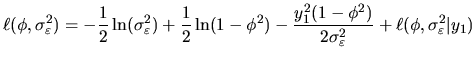
The
ariols
quantlet may be applied to compute the linear LS
estimates of pure ![]() process such as the
process such as the ![]() model (4.49).
In this case we use the code ar2=ariols(z,p, d, "constant")
with
model (4.49).
In this case we use the code ar2=ariols(z,p, d, "constant")
with ![]() and the results are stored in the object ar2. The
first three elements are the basic results: ar2.b is the vector of
parameter estimates (
and the results are stored in the object ar2. The
first three elements are the basic results: ar2.b is the vector of
parameter estimates (
![]() ), ar2.bst is the vector of their corresponding
asymptotic standard errors and ar2.wnv is the innovation variance
estimate
), ar2.bst is the vector of their corresponding
asymptotic standard errors and ar2.wnv is the innovation variance
estimate
![]() . The last three components ar2.checkr, ar2.checkp and ar2.models are lists that include
the diagnostic checking statistics and model selection criteria when the
optional strings rcheck, pcheck and ic are included
and take zero value otherwise.
. The last three components ar2.checkr, ar2.checkp and ar2.models are lists that include
the diagnostic checking statistics and model selection criteria when the
optional strings rcheck, pcheck and ic are included
and take zero value otherwise.
The ![]() model (4.50) is estimated by conditional nonlinear LS
with the
arimacls
quantlet. The basic results of the code ma1=arimacls(z,p,d,q, "constant") with
model (4.50) is estimated by conditional nonlinear LS
with the
arimacls
quantlet. The basic results of the code ma1=arimacls(z,p,d,q, "constant") with
![]() consist of: the vector
ma1.b of the estimated parameters, the innovation variance
estimate ma1.wnv and the vector ma1.conv with the number of
iterations and a 0-1 scalar indicating convergence. The other output
results, ar2.checkr and ar2.ic, are the same as the ariols components.
consist of: the vector
ma1.b of the estimated parameters, the innovation variance
estimate ma1.wnv and the vector ma1.conv with the number of
iterations and a 0-1 scalar indicating convergence. The other output
results, ar2.checkr and ar2.ic, are the same as the ariols components.
The exact maximum likelihood estimation of the
![]() process (4.51) can be done by applying the quantlet
arima11
. The corresponding code is arima11=arima11v(z,d,
"constant") with
process (4.51) can be done by applying the quantlet
arima11
. The corresponding code is arima11=arima11v(z,d,
"constant") with ![]() and the output includes the vector of parameter
estimates (
and the output includes the vector of parameter
estimates (
![]() ), the asymptotic
standard errors of ARMA components (
), the asymptotic
standard errors of ARMA components (
![]() ), the
innovation variance estimate
), the
innovation variance estimate
![]() and the
optional results arima11.checkr, arima11.checkp and arima11.ic.
and the
optional results arima11.checkr, arima11.checkp and arima11.ic.
The parameter estimates are summarized in table 4.3.
|
Once we have identified and estimated the candidate ![]() models, we want
to assess the adequacy of the selected models to the data. This model
diagnostic checking step involves both parameter and residual analysis.
models, we want
to assess the adequacy of the selected models to the data. This model
diagnostic checking step involves both parameter and residual analysis.
If the fitted model is adequate, the residuals should be approximately
white noise. So, we should check if the residuals have zero mean and if
they are uncorrelated. The key instruments are the timeplot, the ACF and
the PACF of the residuals. The theoretical ACF and PACF of white noise
processes take value zero for lags ![]() , so if the model is
appropriate most of the coefficients of the sample ACF and PACF should be
close to zero. In practice, we require that about the 95% of these
coefficients should fall within the non-significance bounds. Moreover, the
Ljung-Box statistic (4.42) should take small values, as corresponds
to uncorrelated variables. The degrees of freedom of this statistic take
into account the number of estimated parameters so the statistic test under
, so if the model is
appropriate most of the coefficients of the sample ACF and PACF should be
close to zero. In practice, we require that about the 95% of these
coefficients should fall within the non-significance bounds. Moreover, the
Ljung-Box statistic (4.42) should take small values, as corresponds
to uncorrelated variables. The degrees of freedom of this statistic take
into account the number of estimated parameters so the statistic test under
![]() follows approximately a
follows approximately a
![]() distribution with
distribution with ![]() .
If the model is not appropriate, we expect the correlograms (simple
and partial) of the residuals to depart from white noise suggesting the
reformulation of the model.
.
If the model is not appropriate, we expect the correlograms (simple
and partial) of the residuals to depart from white noise suggesting the
reformulation of the model.
For example, for the ![]() model we can use the code ma1=
arimacls(z,0,0, 1, "constant","rcheck"). This option plots the
residuals with the usual standard error bounds
model we can use the code ma1=
arimacls(z,0,0, 1, "constant","rcheck"). This option plots the
residuals with the usual standard error bounds
![]() and the simple and partial
correlograms of
and the simple and partial
correlograms of
![]() (see
figure 4.17). The output ma1.checkr also
stores the residuals in the vector a, the statistic for
testing
(see
figure 4.17). The output ma1.checkr also
stores the residuals in the vector a, the statistic for
testing
![]() in the scalar stat
and the ACF, Ljung-Box statistic and the PACF in the matrix acfQ.
in the scalar stat
and the ACF, Ljung-Box statistic and the PACF in the matrix acfQ.
With regard to the zero mean condition, the timeplot shows that
the residuals of the ![]() model evolve around zero and this
behavior is supported by the corresponding hypothesis test
model evolve around zero and this
behavior is supported by the corresponding hypothesis test
![]() . The value of the statistic is
. The value of the statistic is
![]() so the hypothesis of zero mean errors is not rejected. We
can see in the correlogram of these residuals in
figure 4.17 that several coefficients are
significant and besides, the correlogram shows a decaying
sine-cosine wave. The Ljung-Box statistics for some
so the hypothesis of zero mean errors is not rejected. We
can see in the correlogram of these residuals in
figure 4.17 that several coefficients are
significant and besides, the correlogram shows a decaying
sine-cosine wave. The Ljung-Box statistics for some ![]() take the
following values:
take the
following values:
![]() and
and
![]() ,
rejecting the required hypothesis of uncorrelated errors. These
results lead us to reformulate the model.
,
rejecting the required hypothesis of uncorrelated errors. These
results lead us to reformulate the model.
Next, we will check the adequacy of the AR(2) model (4.49) to
![]() data by means of the code ar2=ariols(z,2,0, "constant",
"rcheck"). The output ar2.checkr provides us with the same
results as the
arimacls
, namely, ar2.checkr.a, ar2.checkr.stat, and ar2.checkr.acfQ. Most of the coefficients of
the ACF lie under the non-significance bounds and the Ljung-Box statistic
takes values
data by means of the code ar2=ariols(z,2,0, "constant",
"rcheck"). The output ar2.checkr provides us with the same
results as the
arimacls
, namely, ar2.checkr.a, ar2.checkr.stat, and ar2.checkr.acfQ. Most of the coefficients of
the ACF lie under the non-significance bounds and the Ljung-Box statistic
takes values
![]() and
and
![]() . Then the hypothesis
of uncorrelated errors is not rejected in any case.
. Then the hypothesis
of uncorrelated errors is not rejected in any case.
Finally, the residual diagnostics for the ![]() model (4.51)
are computed with the optional string "rcheck" of the code arma11=arima11(z,0, "constant", "rcheck"). These results show that, given
a significance level of 5%, both hyphotesis of uncorrelated errors and
zero mean errors are not rejected.
model (4.51)
are computed with the optional string "rcheck" of the code arma11=arima11(z,0, "constant", "rcheck"). These results show that, given
a significance level of 5%, both hyphotesis of uncorrelated errors and
zero mean errors are not rejected.
The usual t-statistics to test the statistical significance of the
![]() and
and ![]() parameters should be carried out to check if the
model is overspecified. But it is important, as well, to assess
whether the stationarity and invertibility conditions are
satisfied. If we factorize de
parameters should be carried out to check if the
model is overspecified. But it is important, as well, to assess
whether the stationarity and invertibility conditions are
satisfied. If we factorize de ![]() and
and ![]() polynomials:
polynomials:
An inspection of the covariance matrix of the estimated parameters allows us to detect the possible presence of high correlation between the estimates of some parameters which can be a manifestation of the presence of a 'common factor' in the model (Box and Jenkins; 1976).
The ariols output stores the t-statistics in the vector ar2.checkp.bt, the estimate of the asymptotic covariance matrix in ar2.checkp.bvar and the result of checking the necessary condition for
stationarity (4.16) in the string ar2.checkp.est. When the
process is stationary, this string takes value 0 and in other case a
warning message appears. The arima11 output also checks the
stationary and invertibility conditions of the estimated model and stores
the t-statistics and the asymptotic covariance matrix of the ![]() parameters
parameters
![]() .
.
The following table shows the results for the ![]() model:
model:
[1,] " ln(Minks), AR(2) model " [2,] " Parameter Estimate t-ratio " [3,] "_____________________________________________" [4,] " delta 4.434 3.598" [5,] " phi1 0.877 6.754" [6,] " phi2 -0.288 -2.125"
It can be observed that the parameters of the ![]() model are
statistically significant and the roots of the polynomial
model are
statistically significant and the roots of the polynomial
![]() are
are
![]() , indicating that the stationarity
condition is clearly satisfied. Then, the
, indicating that the stationarity
condition is clearly satisfied. Then, the ![]() seems to be an
appropriate model for the
seems to be an
appropriate model for the
![]() series. Similar results are obtained
for the
series. Similar results are obtained
for the ![]() model.
model.
Once a set of models have been identified and estimated, it is possible that more than one of them is not rejected in the diagnostic checking step. Although we may want to use all models to check which performs best in forecasting, usually we want to select between them. In general, the model which minimizes a certain criterion function is selected.
The standard goodness of fit criterion in Econometrics is the coefficient of determination:
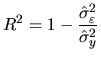
Due to the limitations of the ![]() coefficient, a number of criteria have
been proposed in the literature to evaluate the fit of the model versus
the number of parameters (see Postcher and Srinivasan (1994) for a survey). These
criteria were developed for pure
coefficient, a number of criteria have
been proposed in the literature to evaluate the fit of the model versus
the number of parameters (see Postcher and Srinivasan (1994) for a survey). These
criteria were developed for pure ![]() models but have been extended for
models but have been extended for
![]() models. It is assumed that the degree of differencing has been
decided and that the object of the criterion is to determine the most
appropiate values of
models. It is assumed that the degree of differencing has been
decided and that the object of the criterion is to determine the most
appropiate values of ![]() and
and ![]() . The more applied model selection
criteria are the Akaike Information Criterion,
. The more applied model selection
criteria are the Akaike Information Criterion, ![]() , (Akaike; 1974) and
the Schwarz Information Criterion,
, (Akaike; 1974) and
the Schwarz Information Criterion, ![]() , (Schwarz; 1978) given by:
, (Schwarz; 1978) given by:
| *[1mm]
|
-2.510 | -2.501 |
| -2.440 | -2.432 |
Both criteria select the ![]() model and we use this model to forecast.
This model generates a cyclical behavior of period equal to 10,27 years.
The forecast function of this model for the
model and we use this model to forecast.
This model generates a cyclical behavior of period equal to 10,27 years.
The forecast function of this model for the
![]() series
can be seen in figure 4.18.
series
can be seen in figure 4.18.
To illustrate the time series modelling methodology we have presented so far, we analyze a quarterly, seasonally adjusted series of the European Union G.D.P. from the first quarter of 1962 until the first quarter of 2001 (157 observations).
|
This series is plotted in the first graphic of
figure 4.19. It can be observed that the ![]() series displays a nonstationary pattern with an upward trending
behavior. Moreover, the shape of the correlograms (left column of
figure 4.19) is typical of a nonstationary
process with a slow decay in the ACF and a coefficient
series displays a nonstationary pattern with an upward trending
behavior. Moreover, the shape of the correlograms (left column of
figure 4.19) is typical of a nonstationary
process with a slow decay in the ACF and a coefficient
![]() close to unity in the PACF. The ADF test-values
(see table 4.4) do not reject the unit-root null
hypothesis both under the alternative of a stationary process in
deviations to a constant or to a linear trend. Furthermore the
KPSS statistics clearly reject the null hypothesis of stationarity
around a constant or a linear trend. Thus, we should analyze the
stationarity of the first differences of the series,
close to unity in the PACF. The ADF test-values
(see table 4.4) do not reject the unit-root null
hypothesis both under the alternative of a stationary process in
deviations to a constant or to a linear trend. Furthermore the
KPSS statistics clearly reject the null hypothesis of stationarity
around a constant or a linear trend. Thus, we should analyze the
stationarity of the first differences of the series,
![]() .
.
The right column of figure 4.19 displays the
timeplot of the differenced series ![]() and its estimated ACF and
PACF. The graph of
and its estimated ACF and
PACF. The graph of ![]() shows a series that moves around a
constant mean with approximately constant variance. The estimated
ACF decreases quickly and the ADF test-value,
shows a series that moves around a
constant mean with approximately constant variance. The estimated
ACF decreases quickly and the ADF test-value,
![]() ,
clearly rejects the unit-root hypothesis against the alternative
of a stationarity process around a constant. Given these results
we may conclude that
,
clearly rejects the unit-root hypothesis against the alternative
of a stationarity process around a constant. Given these results
we may conclude that ![]() is a stationary series.
is a stationary series.
The first coefficients of the ACF of ![]() are statistically
significant and decay as
are statistically
significant and decay as ![]() or
or ![]() models. With regard to
the PACF, its first coefficient is clearly significant and large,
indicating that an
models. With regard to
the PACF, its first coefficient is clearly significant and large,
indicating that an ![]() model could be appropriated for the
model could be appropriated for the
![]() series. But given that the first coefficients show some
decreasing structure and the
series. But given that the first coefficients show some
decreasing structure and the
![]() is statistically
significant, perhaps an
is statistically
significant, perhaps an ![]() model should be tried as well.
With regard to the mean, the value of the statistic for the
hypothesis
model should be tried as well.
With regard to the mean, the value of the statistic for the
hypothesis
![]() is
is ![]() and so we reject the
zero mean hypothesis.
and so we reject the
zero mean hypothesis.
Therefore we will analyze the following two models:
|
Estimation results of the
![]() and
and
![]() models
are summarized in table 4.5 and
figure 4.20. Table 4.5 reports parameter
estimates, t-statistics, zero mean hypothesis test-value, Ljung-Box
statistic values for
models
are summarized in table 4.5 and
figure 4.20. Table 4.5 reports parameter
estimates, t-statistics, zero mean hypothesis test-value, Ljung-Box
statistic values for ![]() and the usual selection model
criteria,
and the usual selection model
criteria, ![]() and
and ![]() , for the two models.
Figure 4.20 shows the plot of the residuals and their
correlograms.
, for the two models.
Figure 4.20 shows the plot of the residuals and their
correlograms.
Both models pass the residual diagnostics with very similar results: the
zero mean hypothesis for the residuals is not rejected and the correlograms
and the Ljung-Box statistics indicate that the residuals behave as white
noise processes. However, the parameters of the
![]() model are
not statistically significant. Given the fact that including an
model are
not statistically significant. Given the fact that including an ![]() term
does not seem to improve the results (see the
term
does not seem to improve the results (see the ![]() and
and ![]() values), we
select the more parsimonious
values), we
select the more parsimonious
![]() model.
model.
Figure 4.21 plots the
point and interval forecasts for the next 5 years generated by this model.
As it was expected, since the model for the ![]() series is integrated
of order one with nonzero constant, the eventual forecast function is a
straight line with positive slope.
series is integrated
of order one with nonzero constant, the eventual forecast function is a
straight line with positive slope.