In this section we make a revision of some concepts that are necessary to understand further developments in the chapter, the purpose is to highlight some of the more important theoretical results in probability, in particular, the concept of the random variable, the probability distribution, and some related results. Note however, that we try to maintain the exposition at an introductory level. For a more formal and detailed expositions of these concepts see Härdle and Simar (1999), Mantzapoulus (1995), Newbold (1996) and Wonacot andWonacot (1990).
A random variable is a function that assigns (real) numbers to the results of an experiment. Each possible outcome of the experiment (i.e. value of the corresponding random variable) occurs with a certain probability. This outcome variable, X, is a random variable because, until the experiment is performed, it is uncertain what value X will take. Probabilities are associated with outcomes to quantify this uncertainty.
A random variable is called discrete if the set of all possible
outcomes
![]() is finite or countable. For a discrete
random variable
is finite or countable. For a discrete
random variable ![]() , a probability density function is defined to
be the function
, a probability density function is defined to
be the function ![]() such that for any real number
such that for any real number ![]() ,
which is a value that
,
which is a value that ![]() can take,
can take, ![]() gives the probability that
the random variable
gives the probability that
the random variable ![]() is equal to
is equal to ![]() . If
. If ![]() is not one of
the values that
is not one of
the values that ![]() can take then
can take then ![]() .
.
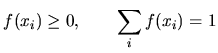
A continuous random variable ![]() can take any value in at least
one interval on the real number line. Assume
can take any value in at least
one interval on the real number line. Assume ![]() can take values
can take values
![]() . Since the possible values of
. Since the possible values of ![]() are uncountable,
the probability associated with any particular point is zero.
Unlike the situation for discrete random variables, the density
function of a continuous random variable will not give the
probability that
are uncountable,
the probability associated with any particular point is zero.
Unlike the situation for discrete random variables, the density
function of a continuous random variable will not give the
probability that ![]() takes the value
takes the value ![]() . Instead, the density
function of a continuous random variable
. Instead, the density
function of a continuous random variable ![]() will be such that
areas under
will be such that
areas under ![]() will give probabilities associated with the
corresponding intervals. The probability density function is
defined so that
will give probabilities associated with the
corresponding intervals. The probability density function is
defined so that
![]() and
and
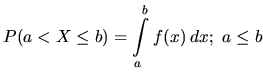 |
(1.1) |
This is the area under ![]() in the range from
in the range from ![]() to
to ![]() . For a
continuous variable
. For a
continuous variable
Cumulative Distribution Function
A function closely related to the probability density function of
a random variable is the corresponding cumulative
distribution function. This function of a discrete random
variable ![]() is defined as follows:
is defined as follows:
That is, ![]() is the probability that the random variable
is the probability that the random variable ![]() takes a value less than or equal to
takes a value less than or equal to ![]() .
.
The cumulative distribution function for a continuous random
variable ![]() is given by
is given by
where ![]() is the the probability density function. In both the
continuous and the discrete case,
is the the probability density function. In both the
continuous and the discrete case, ![]() must satisfy the
following properties:
must satisfy the
following properties:
Expectations of Random Variables
The expected value of a random variable ![]() is the value that we,
on average, expect to obtain as an outcome of the experiment. It
is not necessarily a value actually taken by the random variable.
The expected value, denoted by
is the value that we,
on average, expect to obtain as an outcome of the experiment. It
is not necessarily a value actually taken by the random variable.
The expected value, denoted by ![]() or
or ![]() , is a weighted
average of the values taken by the random variable
, is a weighted
average of the values taken by the random variable ![]() , where the
weights are the respective probabilities.
, where the
weights are the respective probabilities.
Let us consider the discrete random variable ![]() with outcomes
with outcomes
![]() and corresponding probabilities
and corresponding probabilities ![]() . Then,
the expression
. Then,
the expression
defines the expected value of the discrete random variable. For a
continuous random variable ![]() with density
with density ![]() , we define the
expected value as
, we define the
expected value as
Joint Distribution Function
We consider an experiment that consists of two parts, and each
part leads to the occurrence of specified events. We could study
separately both events, however we might be interested in
analyzing them jointly. The probability function defined over a
pair of random variables is called the joint probability
distribution. Consider two random variables X and Y, the joint
probability distribution function of two random variables X and Y
is defined as the probability that X is equal to ![]() at the same
time that Y is equal to
at the same
time that Y is equal to ![]()
If ![]() and
and ![]() are continuous random variables, then the bivariate
probability density function is:
are continuous random variables, then the bivariate
probability density function is:
The counterparts of the requirements for a probability density function are:
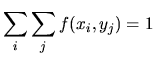 |
|||
| (1.9) | |||
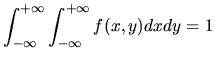 |
The cumulative joint distribution function, in the case that
both ![]() and
and ![]() are discrete random variables is
are discrete random variables is
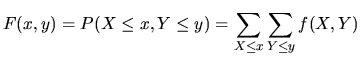 |
(1.10) |
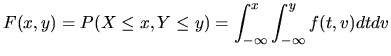 |
(1.11) |
Marginal Distribution Function
Consider now that we know a bivariate random variable ![]() and
its probability distribution, and suppose we simply want to study
the probability distribution of
and
its probability distribution, and suppose we simply want to study
the probability distribution of ![]() , say
, say ![]() . How can we use
the joint probability density function for
. How can we use
the joint probability density function for ![]() to obtain
to obtain
![]() ?
?
The marginal distribution, ![]() , of a discrete random variable
, of a discrete random variable
![]() provides the probability that the variable
provides the probability that the variable ![]() is equal to
is equal to
![]() , in the joint probability
, in the joint probability ![]() , without considering the
variable
, without considering the
variable ![]() , thus, if we want to obtain the marginal distribution
of
, thus, if we want to obtain the marginal distribution
of ![]() from the joint density, it is necessary to sum out the
other variable
from the joint density, it is necessary to sum out the
other variable ![]() . The marginal distribution for the random
variable
. The marginal distribution for the random
variable ![]() ,
, ![]() is defined analogously.
is defined analogously.
The resulting marginal distributions are one-dimensional.
Similarly, we obtain the marginal densities for a pair of continuous random variables X and Y:
Conditional Probability Distribution Function
In the setting of a joint bivariate distribution ![]() ,
consider the case when we have partial information about
,
consider the case when we have partial information about ![]() . More
concretely, we know that the random variable
. More
concretely, we know that the random variable ![]() has taken some
vale
has taken some
vale ![]() . We would like to know the conditional behavior of
. We would like to know the conditional behavior of ![]() given that
given that ![]() has taken the value
has taken the value ![]() . The resultant probability
distribution of
. The resultant probability
distribution of ![]() given
given ![]() is called the conditional
probability distribution function of
is called the conditional
probability distribution function of ![]() given
given ![]() ,
,
![]() . In the discrete case it is defined as
. In the discrete case it is defined as
where ![]() is the conditional probability density function and
is the conditional probability density function and
![]() must be such that
must be such that ![]() . In the continuous case
. In the continuous case
![]() is defined as
is defined as
![]() is the conditional probability density function and
is the conditional probability density function and ![]() must be such that
must be such that ![]() .
.
Conditional Expectation
The concept of mathematical expectation can be applied regardless
of the kind of the probability distribution, then, for a pair of
random variables ![]() with conditional probability density
function, namely
with conditional probability density
function, namely ![]() , the conditional expectation is defined
as the expected value of the conditional distribution, i.e.
, the conditional expectation is defined
as the expected value of the conditional distribution, i.e.
Note that for the discrete case,
![]() are values such
that
are values such
that
![]() .
.
The Regression Function
Let us define a pair of random variables ![]() with a range of
possible values such that the conditional expectation of
with a range of
possible values such that the conditional expectation of ![]() given
given
![]() is correctly defined in several values of
is correctly defined in several values of
![]() .
Then, a regression is just a function that relates different
values of
.
Then, a regression is just a function that relates different
values of ![]() , say
, say
![]() , and their corresponding
values in terms of the conditional expectation
, and their corresponding
values in terms of the conditional expectation
![]() .
.
The main objective of regression analysis is to estimate and
predict the mean value (expectation) for the dependent variable
![]() in base of the given (fixed) values of the explanatory
variable. The regression function describes dependence of a
quantity
in base of the given (fixed) values of the explanatory
variable. The regression function describes dependence of a
quantity ![]() on the quantity
on the quantity ![]() , a one-directional dependence is
assumed. The random variable
, a one-directional dependence is
assumed. The random variable ![]() is referred as regressor,
explanatory variable or independent variable, the random variable
is referred as regressor,
explanatory variable or independent variable, the random variable
![]() is referred as regressand or dependent variable.
is referred as regressand or dependent variable.
In the following Quantlet, we show a two-dimensional random
variable ![]() , we calculate the conditional expectation
, we calculate the conditional expectation
![]() and generate a line by means of merging the values of
the conditional expectation in each
and generate a line by means of merging the values of
the conditional expectation in each ![]() values. The result is
identical to the regression of
values. The result is
identical to the regression of ![]() on
on ![]() .
.
Let us consider ![]() households as the whole population. We want
to know the relationship between the net income and household expenditure, that is, we want a prediction of the
expected expenditure, given the level of net income of the
household. In order to do so, we separate the
households as the whole population. We want
to know the relationship between the net income and household expenditure, that is, we want a prediction of the
expected expenditure, given the level of net income of the
household. In order to do so, we separate the ![]() households in
households in
![]() groups with the same income, then, we calculate the mean
expenditure for every level of income.
groups with the same income, then, we calculate the mean
expenditure for every level of income.
This program produces the output presented in Figure 1.1
The function ![]() is called a regression function.
This function express only the fact that the (population) mean of
the distribution of
is called a regression function.
This function express only the fact that the (population) mean of
the distribution of ![]() given
given ![]() has a functional relationship
with respect to
has a functional relationship
with respect to ![]() .
.
One of the major tasks of statistics is to obtain information
about populations. A population is defined as the set of all
elements that are of interest for a statistical analysis and it
must be defined precisely and comprehensively so that one can
immediately determine whether an element belongs to the population
or not. We denote by ![]() the population size. In fact, in most of
cases, the population is unknown, and for the sake of analysis, we
suppose that it is characterized by a joint probability
distribution function. What is known for the researcher is a
finite subset of observations drawn from this population. This is
called a sample and we will denote the sample size by
the population size. In fact, in most of
cases, the population is unknown, and for the sake of analysis, we
suppose that it is characterized by a joint probability
distribution function. What is known for the researcher is a
finite subset of observations drawn from this population. This is
called a sample and we will denote the sample size by ![]() . The
main aim of the statistical analysis is to obtain information from
the population (its joint probability distribution) through the
analysis of the sample.
. The
main aim of the statistical analysis is to obtain information from
the population (its joint probability distribution) through the
analysis of the sample.
Unfortunately, in many situations the aim of obtaining information about the whole joint probability distribution is too complicated, and we have to orient our objective towards more modest proposals. Instead of characterizing the whole joint distribution function, one can be more interested in investigating one particular feature of this distribution such as the regression function. In this case we will denote it as Population Regression Function (PRF), statistical object that has been already defined in sections 1.1.1 and 1.1.2.
Since very few information is know about the population
characteristics, one has to establish some assumptions about what
is the behavior of this unknown quantity. Then, if we consider the
observations in Figure 1.1 as the the whole
population, we can state that the PRF is a linear function of the
different values of ![]() , i.e.
, i.e.
where ![]() and
and ![]() are fixed unknown parameters which are
denoted as regression coefficients. Note the crucial issue
that once we have determined the functional form of the regression
function, estimation of the parameter values is tantamount to the
estimation of the entire regression function. Therefore, once a
sample is available, our task is considerably simplified since, in
order to analyze the whole population, we only need to give
correct estimates of the regression parameters.
are fixed unknown parameters which are
denoted as regression coefficients. Note the crucial issue
that once we have determined the functional form of the regression
function, estimation of the parameter values is tantamount to the
estimation of the entire regression function. Therefore, once a
sample is available, our task is considerably simplified since, in
order to analyze the whole population, we only need to give
correct estimates of the regression parameters.
One important issue related to the Population Regression Function
is the so called Error term in the regression equation. For
a pair of realizations ![]() from the random variable
from the random variable
![]() , we note that
, we note that ![]() will not coincide with
will not coincide with
![]() .
We define as
.
We define as
the error term in the regression function that indicates the
divergence between an individual value ![]() and its conditional
mean,
and its conditional
mean,
![]() . Taking into account equations (1.19) and
(1.20) we can write the following equalities
. Taking into account equations (1.19) and
(1.20) we can write the following equalities
and
This result implies that for ![]() , the divergences of all
values of
, the divergences of all
values of ![]() with respect to the conditional expectation
with respect to the conditional expectation
![]() are averaged out. There are several reasons for the
existence of the error term in the regression:
are averaged out. There are several reasons for the
existence of the error term in the regression:
The PRF is a feature of the so called Data Generating
Process DGP. This is the joint probability distribution that is
supposed to characterize the entire population from which the data
set has been drawn. Now, assume that from the population of ![]() elements characterized by a bivariate random variable
elements characterized by a bivariate random variable ![]() , a
sample of
, a
sample of ![]() elements,
elements,
![]() , is selected.
If we assume that the Population Regression Function (PRF) that
generates the data is
, is selected.
If we assume that the Population Regression Function (PRF) that
generates the data is
then, given any estimator of ![]() and
and ![]() , namely
, namely
![]() and
and
![]() , we can substitute these estimators
into the regression function
, we can substitute these estimators
into the regression function
obtaining the sample regression function (SRF). The relationship between the PRF and SRF is:
where ![]() is denoted the residual.
is denoted the residual.
Just to illustrate the difference between Sample Regression Function and Population Regression Function, consider the data shown in Figure 1.1 (the whole population of the experiment). Let us draw a sample of 9 observations from this population.
This is shown in Figure 1.2. If we assume that the model
which generates the data is
![]() , then using
the sample we can estimate the parameters
, then using
the sample we can estimate the parameters ![]() and
and ![]() .
.
In Figure 1.3 we present the sample, the population
regression function (thick line), and the sample regression
function (thin line). For fixed values of ![]() in the sample, the
Sample Regression Function is going to depend on the sample,
whereas on the contrary, the Population Regression Function will
always take the same values regardless the sample values.
in the sample, the
Sample Regression Function is going to depend on the sample,
whereas on the contrary, the Population Regression Function will
always take the same values regardless the sample values.
With a data generating process (DGP) at hand, then it is possible
to create new simulated data. If ![]() ,
, ![]() and the vector
of exogenous variables
and the vector
of exogenous variables ![]() is known (fixed), a sample of size
is known (fixed), a sample of size ![]() is created by obtaining
is created by obtaining ![]() values of the random variable
values of the random variable ![]() and
then using these values, in conjunction with the rest of the
model, to generate
and
then using these values, in conjunction with the rest of the
model, to generate ![]() values of
values of ![]() . This yields one complete
sample of size
. This yields one complete
sample of size ![]() . Note that this artificially generated set of
sample data could be viewed as an example of real-world data that
a researcher would be faced with when dealing with the kind of
estimation problem this model represents. Note especially that the
set of data obtained depends crucially on the particular set of
error terms drawn. A different set of error terms would create a
different data set of
. Note that this artificially generated set of
sample data could be viewed as an example of real-world data that
a researcher would be faced with when dealing with the kind of
estimation problem this model represents. Note especially that the
set of data obtained depends crucially on the particular set of
error terms drawn. A different set of error terms would create a
different data set of ![]() for the same problem (see for more
details Kennedy (1998)).
for the same problem (see for more
details Kennedy (1998)).
In order to show how a DGP works, we implement the following
experiment. We generate three replicates of sample ![]() of the
following data generating process:
of the
following data generating process:
![]() .
. ![]() is
generated by a uniform distribution as follows
is
generated by a uniform distribution as follows
![]() .
.
This code produces the values of ![]() , which are the same for the
three samples, and the corresponding values of
, which are the same for the
three samples, and the corresponding values of ![]() , which of
course differ from one sample to the other.
, which of
course differ from one sample to the other.