14.6 Frequency Shift

The goal of this section is to demonstrate how the wavelet transform reflects the properties of the signal simultaneously in frequency and time domains. We consider the signal composed from two sine waves having different frequencies on the time intervals $[0,0.5]$ and $(0.5,1]$, respectively.

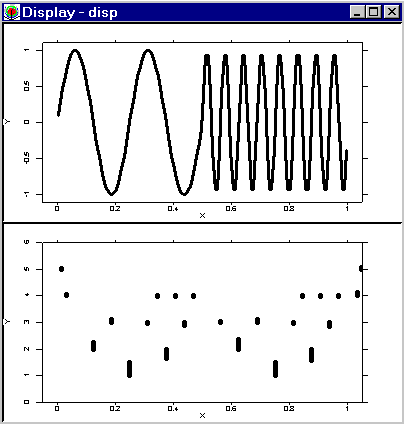
The upper plot in the display above shows the function which consists of two sine waves with different frequencies. The lower plot shows the magnitude of the wavelet coefficients with respect to their location in the time domain ($x$-axis) and the resolution scale ($y$-axis). The magnitude of the wavelet coefficient is proportional to the length of the bar.

The time-frequency structure of the signal is well reflected by the distribution of the wavelet coefficients. To change the number of father wavelet coefficients use the Change level item in the interactive menu.

Looking at the first resolution scale we see that the first two coefficients are greater than the second ones. This is not surprising since the input signal has low frequency at the first time interval and high frequency at the second one. On the other hand, this reflects a good allocation of the mother functions on coarse scales in time domain. The corresponding mother coefficients associated with the wavelet expansion on the right part of the unit interval are sufficiently small because they are inner products of highly oscillating functions (signal) and a sufficiently ``smooth'' function with finite support (wavelet).

Increasing the resolution scale changes the picture significantly. The wavelet coefficients at the left part of the time domain become small. In this case the mother coefficients are inner products of a smooth function (input signal) and a highly oscillating functions (mother functions). At the same time we observe the increase of wavelet coefficients associated with the time domain on the right, where the input signal has a high frequency.

In this example we clearly see that the wavelet decomposition reflects well the properties of the signal in frequency and time domain. This is not the case for the ordinary Fourier transform which reflects only the frequency properties of the signal.

Using the menu you can change father and mother functions by the Change basis item. The use of higher-order wavelets increases the support of father and mother functions and improves the allocation of these functions in the frequency domain. This leads to a better approximation of the smooth parts of the signal. At the same time the approximation of the signal in a neighborhood of discontinuities becomes worse.

• Change basis -- changes the type of the wavelet decomposition. Possible choices are Haar, Daubechies 4, Coiflet 2
• Change level -- changes the number of the father wavelet coefficients on the first resolution scale. This number must be a power of 2 in the range $1,\dots,n/2$
• Change view -- provides other views to the mother wavelet coefficients
• Print -- prints the display