The associations between two sets of variables may be identified and quantified
by canonical correlation analysis. The technique was
originally developed by Hotelling (1935) who analyzed how
arithmetic speed and arithmetic power are related to reading
speed and reading power. Other examples are the relation between
governmental policy variables and economic performance variables and
the relation between job and company characteristics.
Suppose we are given two random variables
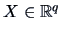 and
and
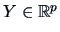 .
The idea is to find an index describing a (possible) link between
.
The idea is to find an index describing a (possible) link between 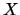 and
and 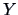 .
Canonical correlation analysis (CCA) is based on linear indices, i.e., linear
combinations
.
Canonical correlation analysis (CCA) is based on linear indices, i.e., linear
combinations
of the random variables.
Canonical correlation analysis searches for vectors 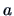 and
and 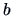 such that the relation of the
two indices
such that the relation of the
two indices 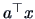 and
and 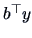 is quantified in some interpretable way.
More precisely, one is looking for the ``most interesting''
projections
is quantified in some interpretable way.
More precisely, one is looking for the ``most interesting''
projections 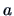 and
and 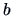 in the sense that they maximize
the correlation
in the sense that they maximize
the correlation
 |
(14.1) |
between the two indices.
Let us consider the correlation 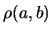 between the two projections
in more detail. Suppose that
between the two projections
in more detail. Suppose that
where the sub-matrices of this covariance structure are given by
Using (3.7) and (4.26),
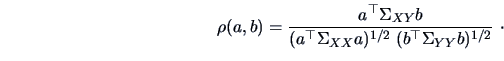 |
(14.2) |
Therefore,
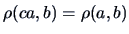 for any
for any
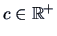 .
Given the invariance of scale we may rescale projections
.
Given the invariance of scale we may rescale projections 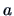 and
and 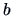 and thus we can equally solve
and thus we can equally solve
under the constraints
For this problem, define
 |
(14.3) |
Recall the singular value decomposition of
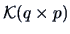 from
Theorem 2.2.
The matrix
from
Theorem 2.2.
The matrix 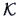 may be decomposed as
may be decomposed as
with
where by (14.3) and (2.15),
and
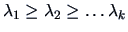 are the
nonzero eigenvalues of
are the
nonzero eigenvalues of
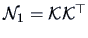 and
and
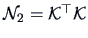 and
and 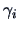 and
and 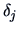 are the standardized
eigenvectors of
are the standardized
eigenvectors of 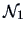 and
and 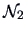 respectively.
respectively.
Define now for 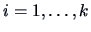 the vectors
the vectors
which are called the canonical correlation vectors.
Using these canonical correlation vectors we define the
canonical correlation variables
The quantities
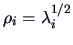 for
for 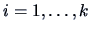 are called the canonical correlation coefficients.
are called the canonical correlation coefficients.
From the properties of the singular value decomposition given in
(14.4) we have
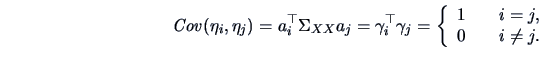 |
(14.9) |
The same is true for
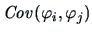 .
The following theorem tells us that the canonical correlation vectors are the solution to the
maximization problem of (14.1).
.
The following theorem tells us that the canonical correlation vectors are the solution to the
maximization problem of (14.1).
THEOREM 14.1
For any given
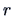
,
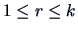
, the maximum
 |
(14.10) |
subject to
and
is given by
and is attained when
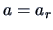
and
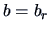
.
PROOF:
The proof is given in three steps.
(i) Fix 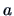 and maximize over
and maximize over 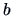 , i.e., solve:
, i.e., solve:
subject to
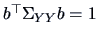 .
By Theorem 2.5 the maximum is given by the largest
eigenvalue of the matrix
.
By Theorem 2.5 the maximum is given by the largest
eigenvalue of the matrix
By Corollary 2.2, the only nonzero eigenvalue equals
 |
(14.11) |
(ii) Maximize (14.11) over 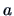 subject to the
constraints of the Theorem. Put
subject to the
constraints of the Theorem. Put
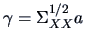 and observe that (14.11) equals
and observe that (14.11) equals
Thus, solve the equivalent problem
 |
(14.12) |
subject to
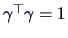 ,
,
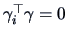 for
for
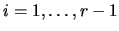 .
.
Note that the 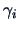 's are the eigenvectors of
's are the eigenvectors of 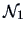 corresponding to its first
corresponding to its first 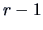 largest eigenvalues. Thus, as
in Theorem 9.3, the maximum in (14.12) is
obtained by setting
largest eigenvalues. Thus, as
in Theorem 9.3, the maximum in (14.12) is
obtained by setting 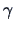 equal to the eigenvector corresponding
to the
equal to the eigenvector corresponding
to the 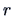 -th largest eigenvalue, i.e.,
-th largest eigenvalue, i.e.,
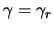 or equivalently
or equivalently
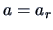 . This yields
. This yields
(iii)
Show that the maximum is attained for 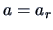 and
and 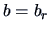 . From the
SVD of
. From the
SVD of 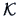 we conclude that
we conclude that
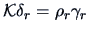 and hence
and hence

Let
The canonical correlation vectors
maximize the correlation between the canonical
variables
The covariance of the canonical variables 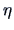 and
and 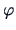 is given
in the next theorem.
is given
in the next theorem.
THEOREM 14.2
Let
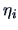
and
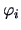
be the
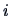
-th canonical correlation variables
(
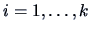
). Define
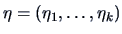
and
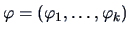
. Then
with
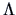
given in (
14.4).
This theorem shows that the canonical correlation coefficients,
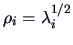 , are the covariances
between the canonical variables
, are the covariances
between the canonical variables 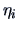 and
and 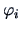 and that
the indices
and that
the indices
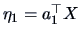 and
and
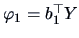 have the
maximum covariance
have the
maximum covariance
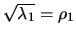 .
.
The following theorem shows that canonical correlations are
invariant w.r.t. linear transformations of the original variables.
THEOREM 14.3
Let
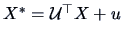
and
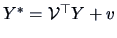
where
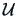
and
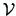
are nonsingular matrices.
Then the canonical correlations between
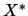
and
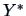
are the same as
those between
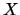
and
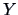
.
The canonical correlation vectors of
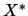
and
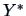
are given by
Summary
-
Canonical correlation analysis aims to identify possible links
between two (sub-)sets of variables
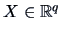 and
and
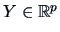 .
The idea is to find indices
.
The idea is to find indices 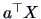 and
and 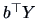 such that the
correlation
such that the
correlation
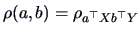 is maximal.
is maximal.
-
The maximum correlation (under constraints) is attained by setting
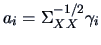 and
and
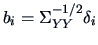 , where
, where 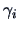 and
and
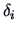 denote the eigenvectors of
denote the eigenvectors of
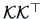 and
and
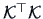 ,
,
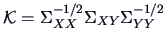 respectively.
respectively.
-
The vectors
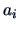 and
and 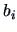 are called canonical correlation vectors.
are called canonical correlation vectors.
-
The indices
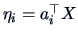 and
and
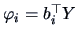 are called
canonical correlation variables.
are called
canonical correlation variables.
-
The values
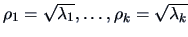 ,
which are the square
roots of the nonzero eigenvalues of
,
which are the square
roots of the nonzero eigenvalues of
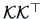 and
and
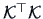 , are called the canonical correlation
coefficients. The covariance between the canonical correlation variables is
, are called the canonical correlation
coefficients. The covariance between the canonical correlation variables is
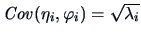 ,
, 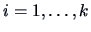 .
.
-
The first canonical variables,
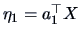 and
and
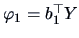 , have the maximum covariance
, have the maximum covariance
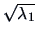 .
.
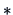
-
Canonical correlations are invariant w.r.t. linear transformations of
the original variables
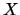 and
and 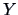 .
.
![]() and
and
![]() .
The idea is to find an index describing a (possible) link between
.
The idea is to find an index describing a (possible) link between ![]() and
and ![]() .
Canonical correlation analysis (CCA) is based on linear indices, i.e., linear
combinations
.
Canonical correlation analysis (CCA) is based on linear indices, i.e., linear
combinations
![]() between the two projections
in more detail. Suppose that
between the two projections
in more detail. Suppose that
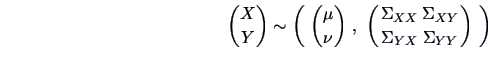
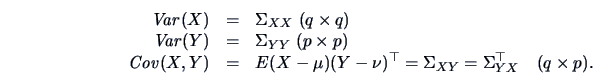
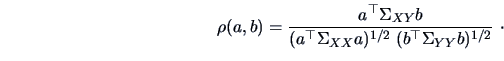


![]() the vectors
the vectors
![]() and maximize over
and maximize over ![]() , i.e., solve:
, i.e., solve:
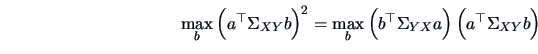
![]() subject to the
constraints of the Theorem. Put
subject to the
constraints of the Theorem. Put
![]() and observe that (14.11) equals
and observe that (14.11) equals
![]() 's are the eigenvectors of
's are the eigenvectors of ![]() corresponding to its first
corresponding to its first ![]() largest eigenvalues. Thus, as
in Theorem 9.3, the maximum in (14.12) is
obtained by setting
largest eigenvalues. Thus, as
in Theorem 9.3, the maximum in (14.12) is
obtained by setting ![]() equal to the eigenvector corresponding
to the
equal to the eigenvector corresponding
to the ![]() -th largest eigenvalue, i.e.,
-th largest eigenvalue, i.e.,
![]() or equivalently
or equivalently
![]() . This yields
. This yields
![]() and
and ![]() . From the
SVD of
. From the
SVD of ![]() we conclude that
we conclude that
![]() and hence
and hence
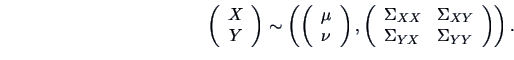
![]() and
and ![]() is given
in the next theorem.
is given
in the next theorem.

![]() , are the covariances
between the canonical variables
, are the covariances
between the canonical variables ![]() and
and ![]() and that
the indices
and that
the indices
![]() and
and
![]() have the
maximum covariance
have the
maximum covariance
![]() .
.