In order to make an 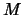 -type kernel estimate scale invariant, it must
be coupled with an estimate of scale. This coupling can be done by
simultaneously estimating the regression and the scale curve.
To fix ideas, assume that
-type kernel estimate scale invariant, it must
be coupled with an estimate of scale. This coupling can be done by
simultaneously estimating the regression and the scale curve.
To fix ideas, assume that
with an unknown 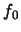 and regression curve
and regression curve 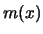 and scale curve
and scale curve 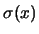 .
Define, for the moment,
.
Define, for the moment,
and
Also
define for
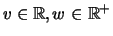 and fixed
and fixed
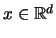 ,
,
The curves
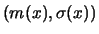 satisfy by definition
satisfy by definition
In practice, one does not know
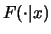 and hence cannot compute
and hence cannot compute 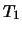 or
or 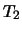 . The approach taken is
to replace
. The approach taken is
to replace
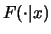 by
by
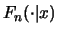 , a kernel estimate of
the conditional distribution function, and to assume that
, a kernel estimate of
the conditional distribution function, and to assume that 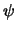 and
and 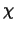 are bounded functions to achieve desirable robustness properties.
Huber (1981, chapter 6.4)
gives examples of functions
are bounded functions to achieve desirable robustness properties.
Huber (1981, chapter 6.4)
gives examples of functions 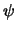 and
and
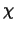 . One of them is
. One of them is
with
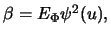 where
where 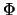 denotes the standard
normal distribution. Consistency for the scale estimate may be obtained
for the normal model:
Under the assumption that the error is standard normally distributed,
the functions
denotes the standard
normal distribution. Consistency for the scale estimate may be obtained
for the normal model:
Under the assumption that the error is standard normally distributed,
the functions 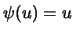 and
and
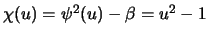 give the conditional mean as regression curve
give the conditional mean as regression curve 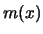 and the
conditional standard deviation as scale curve
and the
conditional standard deviation as scale curve 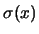 . In fact, the
parameter
. In fact, the
parameter 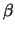 plays the role of a normalizing constant:
If one wishes to
``interpret" the scale curve with respect to some other distribution
plays the role of a normalizing constant:
If one wishes to
``interpret" the scale curve with respect to some other distribution
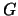 different from the normal
different from the normal 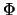 , one can
set
, one can
set
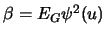 .
.
The functions 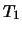 and
and 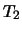 can be estimated by Nadaraya-Watson
kernel weights
can be estimated by Nadaraya-Watson
kernel weights
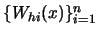 (as in 3.1.1)
(as in 3.1.1)
Call a joint solution of
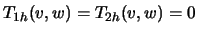 a resistant
regression and scale curve smoother
a resistant
regression and scale curve smoother
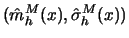 .
Consistency and asymptotic normality of this smoother were shown under
regularity conditions on the kernel and the functions
.
Consistency and asymptotic normality of this smoother were shown under
regularity conditions on the kernel and the functions
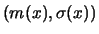 in Härdle and Tsybakov (1988).
Optimization of the smoothing parameter for this procedure was considered by
Tsybakov (1987).
in Härdle and Tsybakov (1988).
Optimization of the smoothing parameter for this procedure was considered by
Tsybakov (1987).
![]() -type kernel estimate scale invariant, it must
be coupled with an estimate of scale. This coupling can be done by
simultaneously estimating the regression and the scale curve.
To fix ideas, assume that
-type kernel estimate scale invariant, it must
be coupled with an estimate of scale. This coupling can be done by
simultaneously estimating the regression and the scale curve.
To fix ideas, assume that
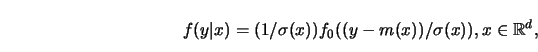


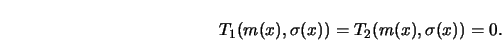
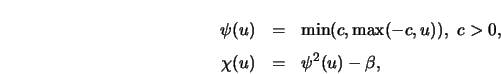
![]() and
and ![]() can be estimated by Nadaraya-Watson
kernel weights
can be estimated by Nadaraya-Watson
kernel weights
![]() (as in 3.1.1)
(as in 3.1.1)