Aktienkurse sind an sich stochastische Prozesse in diskreter Zeit,
die wegen der eingeschränkten Messgenauigkeit auch nur diskrete Werte
annehmen. Dennoch werden oft stochastische Prozesse in stetiger Zeit als
Modelle benutzt, da sie rechnerisch nicht so aufwändig wie diskrete
Modelle - z.B. der Binomial- oder Trinomialprozess - sind. Letztere sind
jedoch oft anschaulicher und sind besonders nützlich für Simulationen.
Der allgemeine Wiener-Prozess
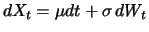 eignet sich selbst weniger als Aktienkursmodell, da er zum einen negative
Aktienkurse zulassen würde, zum anderen die lokale Variabilität größer
ist, wenn der Kurs selbst sich auf hohem Niveau bewegt. Daher wird in
einem allgemeinen Ansatz der Börsenkurs
eignet sich selbst weniger als Aktienkursmodell, da er zum einen negative
Aktienkurse zulassen würde, zum anderen die lokale Variabilität größer
ist, wenn der Kurs selbst sich auf hohem Niveau bewegt. Daher wird in
einem allgemeinen Ansatz der Börsenkurs  einer Aktie als
Itô-Prozess modelliert:
einer Aktie als
Itô-Prozess modelliert:
Dieses Modell hängt von den nicht von vorneherein
bekannten Funktionen
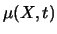 und
und
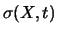 ab. Eine brauchbare, einfache Variante, in der nur noch zwei reellwertige
Modellparameter
ab. Eine brauchbare, einfache Variante, in der nur noch zwei reellwertige
Modellparameter 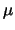 und
und  unbekannt sind, erhält man durch
folgende Überlegung: Die Rendite als prozentualer Zuwachs des eingesetzten
Kapitals soll im Mittel nicht vom aktuellen Kurs bei Kauf der Aktien und
schon gar nicht von der Einheit abhängen (EUR, USD, ...), in der der
Aktienwert gemessen wird. Außerdem soll die mittlere Rendite wie bei
anderen Anlageformen proportional zur Länge des Anlagezeitraums sein.
Zusammen ergibt sich die Forderung
Da
unbekannt sind, erhält man durch
folgende Überlegung: Die Rendite als prozentualer Zuwachs des eingesetzten
Kapitals soll im Mittel nicht vom aktuellen Kurs bei Kauf der Aktien und
schon gar nicht von der Einheit abhängen (EUR, USD, ...), in der der
Aktienwert gemessen wird. Außerdem soll die mittlere Rendite wie bei
anderen Anlageformen proportional zur Länge des Anlagezeitraums sein.
Zusammen ergibt sich die Forderung
Da
![$ \mathop{\text{\rm\sf E}}[dW_t] = 0, $](sfmimg737.gif) ist diese Bedingung bei gegebenem Ausgangskurs
ist diese Bedingung bei gegebenem Ausgangskurs
 erfüllt, wenn
Darüberhinaus wird analog angesetzt:
was die Tatsache berücksichtigt, dass die absolute Größe der Fluktuationen
des Kurses sich proportional ändert, wenn wir den Kurs in einer anderen
Einheit messen. Zusammengefasst modellieren wir den Aktienkurs
erfüllt, wenn
Darüberhinaus wird analog angesetzt:
was die Tatsache berücksichtigt, dass die absolute Größe der Fluktuationen
des Kurses sich proportional ändert, wenn wir den Kurs in einer anderen
Einheit messen. Zusammengefasst modellieren wir den Aktienkurs  als Lösung der stochastischen Differentialgleichung
als Lösung der stochastischen Differentialgleichung
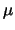 ist die zu erwartende Aktienrendite,
ist die zu erwartende Aktienrendite,
 die Volatilität.
Ein solcher Prozess
die Volatilität.
Ein solcher Prozess
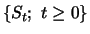 heißt geometrische Brownsche Bewegung,
da
Mit Itôs Lemma, welches wir im Abschnitt 5.5 vorstellen, lässt sich zeigen, dass für einen passenden
allgemeinen Wiener-Prozess
heißt geometrische Brownsche Bewegung,
da
Mit Itôs Lemma, welches wir im Abschnitt 5.5 vorstellen, lässt sich zeigen, dass für einen passenden
allgemeinen Wiener-Prozess
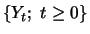
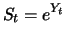
bzw.
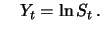
Da 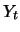 normalverteilt ist, ist
normalverteilt ist, ist  somit lognormalverteilt.
So wie
Irrfahrten diskrete Approximationen für den allgemeinen Wiener-Prozess
liefern, lässt sich die geometrische Brownsche Bewegung, d.h. das einfache
Modell für den Aktienkurs, durch geometrische Irrfahrten annähern.
somit lognormalverteilt.
So wie
Irrfahrten diskrete Approximationen für den allgemeinen Wiener-Prozess
liefern, lässt sich die geometrische Brownsche Bewegung, d.h. das einfache
Modell für den Aktienkurs, durch geometrische Irrfahrten annähern.
Abb.:
Vergleich der Dichten von lognormal und normal
verteilten Zufallsgrößen
 SFMLogNormal.xpl
SFMLogNormal.xpl
|
|
![]() eignet sich selbst weniger als Aktienkursmodell, da er zum einen negative
Aktienkurse zulassen würde, zum anderen die lokale Variabilität größer
ist, wenn der Kurs selbst sich auf hohem Niveau bewegt. Daher wird in
einem allgemeinen Ansatz der Börsenkurs
eignet sich selbst weniger als Aktienkursmodell, da er zum einen negative
Aktienkurse zulassen würde, zum anderen die lokale Variabilität größer
ist, wenn der Kurs selbst sich auf hohem Niveau bewegt. Daher wird in
einem allgemeinen Ansatz der Börsenkurs ![]() einer Aktie als
Itô-Prozess modelliert:
einer Aktie als
Itô-Prozess modelliert:
![$\displaystyle \frac{\mathop{\text{\rm\sf E}}[dS_t]}{S_t} \, = \, \frac{\mathop{\text{\rm\sf E}}[S_{t+dt} - S_t]}{S_t} \, = \,
\mu \cdot dt . $](sfmimg736.gif)
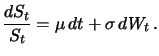
![\includegraphics[width=1\defpicwidth]{distrib.ps}](sfmimg745.gif)