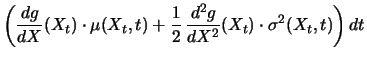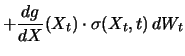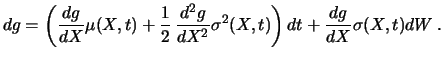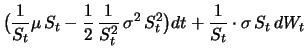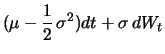Ein entscheidendes Hilfsmittel beim Umgang mit stochastischen
Differentialgleichungen ist das Lemma von Itô. Ist
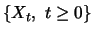 ein Itô-Prozess:
ein Itô-Prozess:
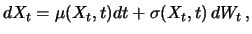 |
(7.8) |
so interessiert man sich oft für den Verlauf anderer stochastischer
Prozesse, die Funktionen von 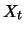 sind:
sind:
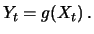
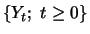 lässt sich dann ebenfalls als Lösung einer
stochastischen Differentialgleichung beschreiben, und aus dieser Gleichung
lassen sich interessierende Eigenschaften von
lässt sich dann ebenfalls als Lösung einer
stochastischen Differentialgleichung beschreiben, und aus dieser Gleichung
lassen sich interessierende Eigenschaften von 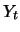 wie z.B. das mittlere
Wachstum mit der Zeit
wie z.B. das mittlere
Wachstum mit der Zeit  ablesen.
ablesen.
Um die Gleichung für
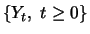 heuristisch herzuleiten,
nehmen wir an, dass
heuristisch herzuleiten,
nehmen wir an, dass 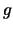 genügend oft differenzierbar ist. Aus der
Taylorreihenentwicklung folgt:
genügend oft differenzierbar ist. Aus der
Taylorreihenentwicklung folgt:
wobei die Punkte für Terme vernachlässigbarer Größenordnung (für
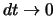 ) stehen. Die für
) stehen. Die für
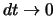 dominanten
Terme in
dominanten
Terme in 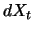 sind aufgrund der Form des Itô Prozesses (5.8) der Driftterm
sind aufgrund der Form des Itô Prozesses (5.8) der Driftterm
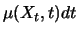 von der Größenordnung
von der Größenordnung 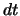 und der Volatilitätsterm
und der Volatilitätsterm
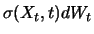 von der Größenordnung
von der Größenordnung 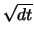 .
.
Dabei berücksichtigen wir
![$ \mathop{\text{\rm\sf E}}[(dW_t)^2] = dt, $](sfmimg761.gif) so dass
so dass
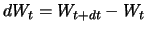 von der Größenordnung seiner
Standardabweichung, also
von der Größenordnung seiner
Standardabweichung, also
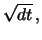 ist. Terme von kleinerer
Größenordnung als
ist. Terme von kleinerer
Größenordnung als 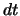 vernachlässigen wir hier bei diesem heuristischen Argument. Daher können wir
vernachlässigen wir hier bei diesem heuristischen Argument. Daher können wir 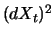 durch einen einfacheren Ausdruck ersetzen:
durch einen einfacheren Ausdruck ersetzen:
Wir sehen, dass der erste Term von der Größenordnung 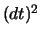 ist. Der zweite ist von der
Größenordnung
ist. Der zweite ist von der
Größenordnung
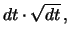 so dass beide vernachlässigt
werden können. Der dritte Term hat allerdings die
Größenordnung
so dass beide vernachlässigt
werden können. Der dritte Term hat allerdings die
Größenordnung 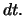 Genauer kann man zeigen, dass für
Genauer kann man zeigen, dass für
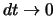 Mit dieser einfachen Identität lassen sich Rechenregeln für stochastische
Differentialgleichungen aus den bekannten Regeln für den Umgang mit
deterministischen Funktionen (wie z.B. der Taylorentwicklung) ableiten.
Unter Vernachlässigung von Termen kleinerer Größenordnung als
Mit dieser einfachen Identität lassen sich Rechenregeln für stochastische
Differentialgleichungen aus den bekannten Regeln für den Umgang mit
deterministischen Funktionen (wie z.B. der Taylorentwicklung) ableiten.
Unter Vernachlässigung von Termen kleinerer Größenordnung als 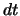 erhalten wir so aus (5.9) die folgende Form von Itôs Lemma:
erhalten wir so aus (5.9) die folgende Form von Itôs Lemma:
Lemma 7.1 (Itôs Lemma)
bzw. - durch Weglassen des Zeitindex

und des Arguments
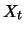
der
Funktion
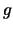
und ihrer Ableitungen:
Beispiel 7.1
Als Beispiel betrachten wir
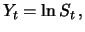
den Logarithmus der
geometrischen Brownschen Bewegung. Für
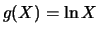
haben wir
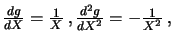
und für die geometrische Brownsche Bewegung ist
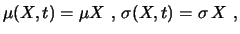
so dass Itôs Lemma ergibt:
Der
Logarithmus des Aktienkurses ist also ein allgemeiner
Wiener-Prozess mit Driftrate
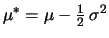
und
Varianzrate
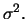
Da
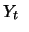
N
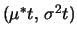
-verteilt ist, ist

selbst
lognormalverteilt mit Parametern
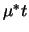
und
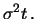
Eine allgemeine Form von Itôs Lemma für Funktionen 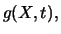 die auch noch von der Zeit
die auch noch von der Zeit  abhängen dürfen,
lautet :
abhängen dürfen,
lautet :
Lemma 7.2 (Itôs Lemma für explizit zeitabhängige Funktionen)
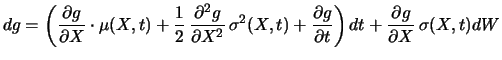 |
(7.10) |
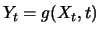 ist also wieder ein Itô-Prozess, wobei als
zusätzlicher Term in der Driftrate
ist also wieder ein Itô-Prozess, wobei als
zusätzlicher Term in der Driftrate
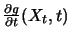 auftaucht.
auftaucht.
![]() ein Itô-Prozess:
ein Itô-Prozess:
![]() heuristisch herzuleiten,
nehmen wir an, dass
heuristisch herzuleiten,
nehmen wir an, dass ![]() genügend oft differenzierbar ist. Aus der
Taylorreihenentwicklung folgt:
genügend oft differenzierbar ist. Aus der
Taylorreihenentwicklung folgt:
![]() so dass
so dass
![]() von der Größenordnung seiner
Standardabweichung, also
von der Größenordnung seiner
Standardabweichung, also
![]() ist. Terme von kleinerer
Größenordnung als
ist. Terme von kleinerer
Größenordnung als ![]() vernachlässigen wir hier bei diesem heuristischen Argument. Daher können wir
vernachlässigen wir hier bei diesem heuristischen Argument. Daher können wir ![]() durch einen einfacheren Ausdruck ersetzen:
durch einen einfacheren Ausdruck ersetzen: