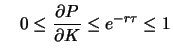In diesem Abschnitt betrachten wir den wichtigen Begriff der Arbitragefreiheit. Unter Arbitrage
verstehen wir einen risikolosen Gewinn. In einem idealen Finanzmarkt, in dem unter anderem alle Investoren
denselben Informationsstand haben und verzögerungsfrei handeln können, sollte es keine Möglichkeiten
zur Arbitrage geben. Jeder Investor würde andernfalls versuchen, einen risikolosen Gewinn augenblicklich
mitzunehmen. Die dadurch ausgelösten Transaktionen würden ebenfalls augenblicklich die Preise der involvierten
Finanzinstrumente so ändern, dass die Arbitragemöglichkeit sofort verschwindet.
Zusätzlich zur Arbitragefreiheit fordern wir in diesem Kapitel,
dass der Finanzmarkt einigen weiteren idealisierenden Annahmen
genügt, die allerdings in diesem Zusammenhang einen geringeren
Stellenwert haben und nur die Argumentation wesentlich
vereinfachen. Sind diese Annahmen erüllt, sprechen wir von einem
perfekt funktionierenden Finanzmarkt.
ANNAHME (perfekter Finanzmarkt)
Es gibt keine Arbitragemöglichkeiten, keine
Transaktionskosten, keine Steuern und keine Einschränkungen beim
Short-selling. Soll- und Habenzinsen sind gleich, und alle
Wertpapiere sind beliebig teilbar.
Die Annahme eines perfekt funktionierenden Finanzmarktes reicht
allein
schon aus, um den Wert von Terminkontrakten
und wichtige Beziehungen zwischen den
Preisen verschiedener Optionen herzuleiten. Vor
allem ist es nicht nötig, ein mathematisches Modell für den
Kurs des Finanzinstruments, das Gegenstand der Optionen oder
Terminkontrakte ist, zu formulieren. Um den Wert von Optionen zu
bestimmen, genügen rein ökonomische Annahmen allerdings nicht
mehr, sondern es ist eine detailliertere mathematische
Modellierung nötig. Jeder mathematische Ansatz muss sich
allerdings an den in diesem Kapitel hergeleiteten
Arbitragebeziehungen messen lassen: wenn das Modell zu anderen
Ergebnissen bei der Bewertung von Terminkontrakten führt und die
aus ihm abgeleiteten Optionspreise nicht den folgenden Relationen
genügen, dann beruht es auf falschen Voraussetzungen.
Eine wichtige Folgerung aus der Annahme eines perfekten Marktes und dabei vor allem aus der Arbitragefreiheit,
die wir in den folgenden Beweisen immer wieder benutzen, ist die Tatsache, dass zwei Portfolios, die zu einem
bestimmten Zeitpunkt  denselben Wert haben, auch zu jedem früheren Zeitpunkt
denselben Wert haben, auch zu jedem früheren Zeitpunkt  wertgleich sind.
Wegen ihrer Bedeutung stellen wir diese Argumentation hier in ihren Einzelheiten vor.
Wir gehen von zwei Portfolios
wertgleich sind.
Wegen ihrer Bedeutung stellen wir diese Argumentation hier in ihren Einzelheiten vor.
Wir gehen von zwei Portfolios  und
und  , die sich aus beliebigen Anlageformen zusammensetzen, aus. Ihr Wert
zur Zeit
, die sich aus beliebigen Anlageformen zusammensetzen, aus. Ihr Wert
zur Zeit  bezeichnen wir mit
bezeichnen wir mit 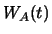 bzw.
bzw. 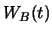 . Wir nehmen für einen festen Zeitpunkt
. Wir nehmen für einen festen Zeitpunkt  an, dass
sicher
an, dass
sicher
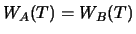 unabhängig von der Wertentwicklung der einzelnen, in
unabhängig von der Wertentwicklung der einzelnen, in  und
und  enthaltenen Anlagen.
Für einen beliebigen früheren Zeitpunkt
enthaltenen Anlagen.
Für einen beliebigen früheren Zeitpunkt 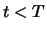 nehmen wir ohne Beschränkung der Allgemeinheit an,
dass
nehmen wir ohne Beschränkung der Allgemeinheit an,
dass
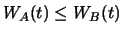 . Ein Investor kann zur Zeit
. Ein Investor kann zur Zeit  ohne Eigenkapitaleinsatz ein kombiniertes Portfolio
aufbauen, indem er eine Einheit aller Anlagen in
ohne Eigenkapitaleinsatz ein kombiniertes Portfolio
aufbauen, indem er eine Einheit aller Anlagen in  kauft, eine Einheit aller Anlagen in
kauft, eine Einheit aller Anlagen in  verkauft (Short-selling)
und den Differenzbetrag
verkauft (Short-selling)
und den Differenzbetrag
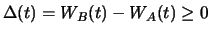 festverzinslich zum Zinssatz
festverzinslich zum Zinssatz 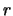 anlegt. Das kombinierte
Portfolio hat zur Zeit
anlegt. Das kombinierte
Portfolio hat zur Zeit  den Wert
den Wert
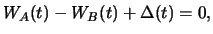
kostet den Investor also nichts. Zur Zeit  hat der festverzinsliche Anteil des kombinierten Portfolios den
aufgezinsten Wert
hat der festverzinsliche Anteil des kombinierten Portfolios den
aufgezinsten Wert
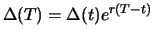 , das Portfolio als Ganzes also sicher den Wert
, das Portfolio als Ganzes also sicher den Wert
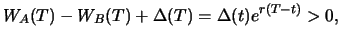
falls
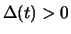 . Der Investor hat mit dem kombinierten
Portfolio also einen sicheren Gewinn gemacht, ohne ein Risiko
einzugehen. Dies ist ein Widerspruch zur angenommenen
Arbitragefreiheit, und daher muss
. Der Investor hat mit dem kombinierten
Portfolio also einen sicheren Gewinn gemacht, ohne ein Risiko
einzugehen. Dies ist ein Widerspruch zur angenommenen
Arbitragefreiheit, und daher muss
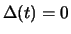 gelten, d.h.
gelten, d.h.
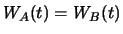 .
.
Diese Argumentation kann nun ausgenutzt werden, um den unbekannten Wert eines Finanzderivats zu bestimmen.
Hierzu wird ein Portfolio  zusammengestellt, dass neben Anlagen mit bekanntem Preis auch eine Einheit des
Derivats enthält. Diesem Portfolio wird ein zweites, sogenanntes Duplikationsportfolio
zusammengestellt, dass neben Anlagen mit bekanntem Preis auch eine Einheit des
Derivats enthält. Diesem Portfolio wird ein zweites, sogenanntes Duplikationsportfolio
 gegenübergestellt, das ausschließlich aus Anlagen mit bekanntem Preis
besteht und so konstruiert worden ist, dass es zu einem festen Zeitpunkt
gegenübergestellt, das ausschließlich aus Anlagen mit bekanntem Preis
besteht und so konstruiert worden ist, dass es zu einem festen Zeitpunkt  sicher denselben Wert wie
sicher denselben Wert wie  hat.
Dann folgt aus der Arbitragefreiheit, dass beide Portfolios zu jedem früheren Zeitpunkt wertgleich sind, und daraus
ergibt sich sofort der Wert des Finanzderivats zu jedem Zeitpunkt
hat.
Dann folgt aus der Arbitragefreiheit, dass beide Portfolios zu jedem früheren Zeitpunkt wertgleich sind, und daraus
ergibt sich sofort der Wert des Finanzderivats zu jedem Zeitpunkt 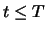 . Wir illustrieren diese Vorgehensweise
am Beispiel eines Terminkontrakts.
. Wir illustrieren diese Vorgehensweise
am Beispiel eines Terminkontrakts.
Satz 4.1
Wir betrachten den Terminkauf eines Objekts, das zur Zeit

den Kurs

hat.

sei der Terminkurs und

der Zeitpunkt der Fälligkeit.
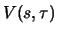
bezeichne den
Wert des Terminkaufs zur Zeit

als Funktion des aktuellen
Kurses
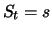
und der verbleibenden Laufzeit
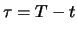
. Wir nehmen an, dass
die Zinsen während der Laufzeit gleich einem konstanten Wert
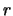
sind.
- Wirft das zugrundeliegende Objekt während der Restlaufzeit
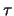 keine Erträge ab und
verursacht es auch keine Kosten, so gilt
keine Erträge ab und
verursacht es auch keine Kosten, so gilt
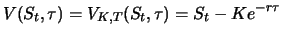 |
(4.1) |
Der Forward-Preis ist in diesem Fall
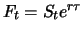 .
.
- Fallen während der Restlaufzeit
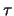 durch das Halten des zugrundeliegenden Objektes zu diskreten
Zeitpunkten Erträge oder Kosten an, deren auf den aktuellen Zeitpunkt
durch das Halten des zugrundeliegenden Objektes zu diskreten
Zeitpunkten Erträge oder Kosten an, deren auf den aktuellen Zeitpunkt  abgezinster Gesamtwert
abgezinster Gesamtwert 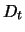 ist,
so gilt
ist,
so gilt
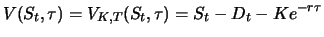 |
(4.2) |
Der Forward-Preis ist in diesem Fall
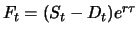 .
.
- Sind mit dem Objekt stetige Bestandshaltekosten mit einer Rate
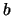 verbunden, so gilt
verbunden, so gilt
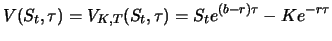 |
(4.3) |
Der Forward-Preis ist in diesem Fall
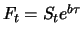 .
.
Beweis:
Wir nennen das zugrundeliegende Objekt der Einfachheit halber eine
Aktie mit diskreten, auf den Zeitpunkt  abgezinsten Dividenden
abgezinsten Dividenden 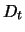 bzw. mit stetigem Dividendenertrag
bzw. mit stetigem Dividendenertrag
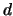 . Im letzteren Fall sind die stetigen Bestandshaltekosten
der Aktie
. Im letzteren Fall sind die stetigen Bestandshaltekosten
der Aktie 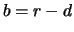 : der Investor
gewinnt durch Halten der Aktie Dividenden (als negative Kosten)
mit der Rate
: der Investor
gewinnt durch Halten der Aktie Dividenden (als negative Kosten)
mit der Rate 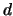 , verliert aber gleichzeitig Zinsen mit der Rate
, verliert aber gleichzeitig Zinsen mit der Rate
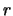 , da er sein Kapital in die Aktie anstelle einer
festverzinslichen Anleihe gesteckt hat. Statt Aktien können
genausogut Anleihen, Devisen oder andere einfache Anlageformen
betrachtet werden.
, da er sein Kapital in die Aktie anstelle einer
festverzinslichen Anleihe gesteckt hat. Statt Aktien können
genausogut Anleihen, Devisen oder andere einfache Anlageformen
betrachtet werden.
1. Wir betrachten zum Zeitpunkt  zwei Portfolios
zwei Portfolios  und
und  , die folgendes Aussehen haben:
, die folgendes Aussehen haben:
- Portfolio
 :
:
- Terminkauf der Aktie zum Terminkurs
 , fällig zum Zeitpunkt
, fällig zum Zeitpunkt  .
.
Kauf eines Zerobonds mit Nominalwert  , fällig zum Zeitpunkt
, fällig zum Zeitpunkt  .
.
- Portfolio
 :
:
- Kauf einer Aktie
Am Ende der Laufzeit zur Zeit  wird in Portfolio
wird in Portfolio  der Zerobond verkauft. Der Erlös
der Zerobond verkauft. Der Erlös  wird benutzt,
um die mit dem Terminkauf eingegangene Verpflichtung zu erfüllen und eine Aktie zum Preis
wird benutzt,
um die mit dem Terminkauf eingegangene Verpflichtung zu erfüllen und eine Aktie zum Preis  zu kaufen.
Danach enthält Portfolio
zu kaufen.
Danach enthält Portfolio  eine Aktie und hat somit zur Zeit
eine Aktie und hat somit zur Zeit  denselben Wert wie Portfolio
denselben Wert wie Portfolio  . Daher gilt
wegen der vorausgesetzten Arbitragefreiheit zum Zeitpunkt
. Daher gilt
wegen der vorausgesetzten Arbitragefreiheit zum Zeitpunkt  ebenfalls Gleichheit, also
ebenfalls Gleichheit, also
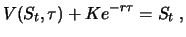 |
(4.4) |
da sich durch Abzinsen als Wert des Zerobonds zur Zeit  gerade
gerade
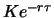 ergibt. Der Forward-Preis ist nach
Definition die Lösung von
2. Wir betrachten zur Zeit
ergibt. Der Forward-Preis ist nach
Definition die Lösung von
2. Wir betrachten zur Zeit  die beiden Portfolios
die beiden Portfolios  und
und  aus dem ersten Teil des Beweises, ergänzen
aus dem ersten Teil des Beweises, ergänzen  aber jetzt um eine Position zu:
aber jetzt um eine Position zu:
- Portfolio
 :
:
- Kauf einer Aktie und leihen eines Geldbetrages in Höhe
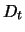 zum Zinssatz
zum Zinssatz 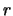 (= Verkauf eines Zerobonds).
(= Verkauf eines Zerobonds).
Zur Zeit  werden in Portfolio
werden in Portfolio  die Dividendenerträge der Aktie - im auf die Zeit
die Dividendenerträge der Aktie - im auf die Zeit  aufgezinsten Wert von
aufgezinsten Wert von
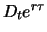 - genutzt, um die Anleihe zurückzuzahlen. Damit besteht Portfolio
- genutzt, um die Anleihe zurückzuzahlen. Damit besteht Portfolio  wie Portfolio
wie Portfolio  zur Zeit
zur Zeit  wieder nur aus einer Aktie, und es ergibt sich wieder Wertgleichheit auch zum Zeitpunkt
wieder nur aus einer Aktie, und es ergibt sich wieder Wertgleichheit auch zum Zeitpunkt  :
:
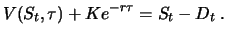 |
(4.5) |
Der Forward-Preis ergibt sich dann wie in Teil 1. aus der
Definition.
3. Besitzt die Aktie eine stetige Dividendenrendite 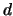 , kann ähnlich argumentiert
werden. Wieder betrachten wir zwei Portfolios
, kann ähnlich argumentiert
werden. Wieder betrachten wir zwei Portfolios  und
und  zum Zeitpunkt
zum Zeitpunkt  ,
wobei
,
wobei  wie im ersten Teil des Beweises gewählt wird. Portfolio
wie im ersten Teil des Beweises gewählt wird. Portfolio  hat folgendes
Aussehen
hat folgendes
Aussehen
- Portfolio
 :
:
- Kauf von
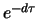 Aktien .
Aktien .
Wird der Dividendenertrag in Portfolio  laufend direkt wieder in die Aktie reinvestiert,
besteht Portfolio
laufend direkt wieder in die Aktie reinvestiert,
besteht Portfolio  auch in diesem Fall zum Zeitpunkt
auch in diesem Fall zum Zeitpunkt  aus genau einer Aktie. Heuristisch sieht
man das folgendermaßen: Im Zeitintervall
aus genau einer Aktie. Heuristisch sieht
man das folgendermaßen: Im Zeitintervall
![$ [t, t+\delta]$](sfmimg155.gif) wirft für kleines
wirft für kleines 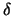 eine Aktie eine Dividende von
approximativ
eine Aktie eine Dividende von
approximativ
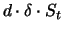 ab, der aktuelle Bestand von
ab, der aktuelle Bestand von
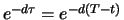 Aktien also eine
Dividende von
Aktien also eine
Dividende von
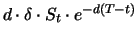 . Dieser Betrag wird in Aktien reinvestiert. Unter der Annahme, dass
sich der Kurs in dem kleinen Zeitintervall
. Dieser Betrag wird in Aktien reinvestiert. Unter der Annahme, dass
sich der Kurs in dem kleinen Zeitintervall
![$ [t, t+\delta]$](sfmimg155.gif) nicht wesentlich ändert, d.h.
nicht wesentlich ändert, d.h.
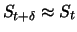 ,
enthält Portfolio
,
enthält Portfolio  zur Zeit
zur Zeit 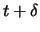 insgesamt
Aktien. Diese Argumentation kann man mit dem Grenzübergang
insgesamt
Aktien. Diese Argumentation kann man mit dem Grenzübergang
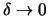 exakt machen und zeigen,
dass Portfolio
exakt machen und zeigen,
dass Portfolio  zu jedem Zeitpunkt
zu jedem Zeitpunkt 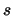 zwischen
zwischen  und
und  genau
genau
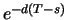 , für
, für 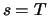 also eine
Aktie enthält. Die gleiche Argumentation wie im ersten Teil des Beweises liefert dann die Wertgleichheit
der beiden Portfolios
also eine
Aktie enthält. Die gleiche Argumentation wie im ersten Teil des Beweises liefert dann die Wertgleichheit
der beiden Portfolios  und
und  zum Zeitpunkt
zum Zeitpunkt  , also
, also
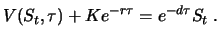 |
(4.6) |
Mit 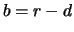 erhalten wir die gewünschte Form. Der Forward-Preis ergibt sich dann wie in Teil 1. aus der Definition.
erhalten wir die gewünschte Form. Der Forward-Preis ergibt sich dann wie in Teil 1. aus der Definition. 
Beispiel 4.1
Wir betrachten den Terminkauf einer 5-Jahres Anleihe, die zum Kurs
900 EUR gehandelt wird. Der Terminkurs betrage 910 EUR, die
Laufzeit des Terminkontraktes ein Jahr. Kouponzahlungen in
Höhe von 60 EUR fallen in 6 bzw. 12 Monaten (letztere kurz vor
Fälligkeit des Kontraktes) an. Der stetige Jahreszins für 6
bzw. 12 Monate betrage 9% bzw. 10%. In diesem Fall ist
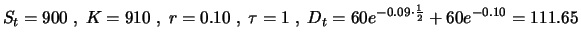 |
(4.7) |
Der Wert des Terminkaufs ist dann
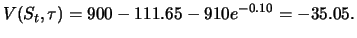 |
(4.8) |
Der Wert der entsprechenden Short-Position ist dann +35.05. Der
Forward-Preis
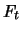
beträgt
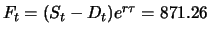
.
Beispiel 4.2
Wir betrachten den Terminkauf von 1000 Dollar. In diesem Fall liegt ein
stetiger Dividendenertrag
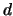
in Höhe des amerikanischen
Zinssatzes vor, wenn der Investor den Dollarbetrag erwirbt und in den USA anlegt.
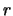
sei der
inländische Zinssatz. Die Bestandshaltekosten
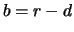
sind die Differenz zwischen Inlands- und
Auslandszinssatz. Bezeichnet

den Dollarkurs, so ist der Forward-Preis dann
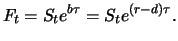 |
(4.9) |
Für
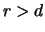
ergibt sich ein Report
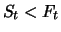
(Zinsaufschlag), für
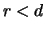
ergibt sich ein
Deport
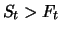
(Zinsabschlag). Ist
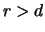
und wählt man den Terminkurs gleich dem aktuellen Kurs, d.h.
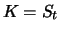
, so ist der Wert des Terminkaufs
Der Terminkauf zum Preis

ist also teurer als der sofortige Kauf zum selben Preis, denn er ermöglicht
dem Investor, noch bis zur Zeit

den aktuell höheren Inlandszinssatz auf seine heimische Währung zu
nutzen.
Das folgende Resultat besagt, dass es keinen Unterschied zwischen
Forward- und Future-Kontrakten mit gleichem Terminkurs und
gleicher Laufzeit gibt, wenn der Zinssatz sich über die ganze
Laufzeit hinweg nicht ändert. Wir benutzen dabei, dass nach
Definition von Forward- und Future-Preis ein Terminkauf nichts
kostet, wenn der Terminkurs gleich dem aktuellen Forward- bzw.
Future-Preis gewählt wird.
Satz 4.2
Ist der Zinssatz während der Laufzeit konstant, so stimmen Future- und Forward-Preis miteinander überein.
Beweis:
Wir gehen davon aus, dass der Future-Kontrakt am Tag 0 geschlossen wird und eine
Gesamtlaufzeit von 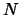 Tagen hat. Wir nehmen an, dass der Gewinn-Verlust-Ausgleich täglich bei einem
Tageszinssatz von
Tagen hat. Wir nehmen an, dass der Gewinn-Verlust-Ausgleich täglich bei einem
Tageszinssatz von 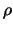 erfolgt .
erfolgt . 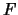 bezeichne den Forward-Preis bei Kontraktbeginn, d.h. am Ende des 0-ten Tages, und
bezeichne den Forward-Preis bei Kontraktbeginn, d.h. am Ende des 0-ten Tages, und
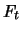 sei der Future-Preis am Ende des
sei der Future-Preis am Ende des  -ten Tages,
-ten Tages,
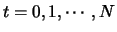 . Unser Ziel ist es,
. Unser Ziel ist es, 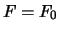 zu zeigen. Dazu
stellen wir wieder zwei Portfolios zusammen:
zu zeigen. Dazu
stellen wir wieder zwei Portfolios zusammen:
- Portfolio
 :
:
- Kauf von
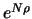 Forward-Kontrakten mit Terminkurs
Forward-Kontrakten mit Terminkurs 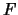 , Laufzeit
, Laufzeit 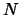 .
.
Kauf eines Zerobonds mit Nominalwert
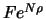 und Fälligkeit in
und Fälligkeit in 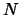 Tagen.
Tagen.
- Portfolio
 :
:
- Täglicher Zukauf von Future-Kontrakten mit
jeweiligem Terminkurs
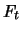 und Fälligkeit zur Zeit
und Fälligkeit zur Zeit 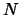 derart, dass am Ende des
derart, dass am Ende des  -ten Tages genau
-ten Tages genau
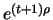 Future-Kontrakte im Portfolio enthalten sind (
Future-Kontrakte im Portfolio enthalten sind (
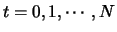 ).
).
Kauf eines Zerobonds mit Nominalwert
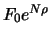 und Fälligkeit in
und Fälligkeit in 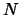 Tagen.
Tagen.
Der Erwerb der Forward- und Future-Kontrakte ist kostenlos, da er
jeweils mit dem Forward- bzw. dem tagesaktuellen Future-Preis als
Terminkurs erfolgt. Der Halter von Portfolio  erhält von Tag
erhält von Tag
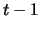 auf den Tag
auf den Tag  durch den Gewinn-Verlust-Ausgleich
durch den Gewinn-Verlust-Ausgleich
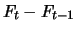 je Future-Kontrakt im Portfolio. Dies kann negativ sein,
d.h. er selbst muss zahlen.
je Future-Kontrakt im Portfolio. Dies kann negativ sein,
d.h. er selbst muss zahlen.
Am Ende der Laufzeit, d.h. des 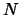 -ten Tages, wird in Portfolio
-ten Tages, wird in Portfolio
 der Ertrag
der Ertrag
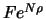 des Zerobonds benutzt, um den
Terminkontrakt zu erfüllen und
des Zerobonds benutzt, um den
Terminkontrakt zu erfüllen und 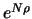 Aktien zum Preis von
jeweils
Aktien zum Preis von
jeweils 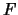 zu kaufen. Das Portfolio
zu kaufen. Das Portfolio  enthält dann nur noch
diese Aktien und hat den Wert
enthält dann nur noch
diese Aktien und hat den Wert
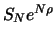 . Wir zeigen nun, dass
dies auch für Portfolio
. Wir zeigen nun, dass
dies auch für Portfolio  gilt.
gilt.
Zu Beginn des Tages  sind
sind 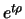 Futures im Portfolio, und
der Halter erhält durch den Gewinn-Verlust-Ausgleich den Betrag
Futures im Portfolio, und
der Halter erhält durch den Gewinn-Verlust-Ausgleich den Betrag
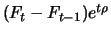 , der auch negativ sein kann. Während
des Tages stockt er kostenfrei, da mit dem aktuellen Future-Preis
als Terminkurs, sein Portfolio um weitere Futures auf, so dass es
am Tagesende insgesamt
, der auch negativ sein kann. Während
des Tages stockt er kostenfrei, da mit dem aktuellen Future-Preis
als Terminkurs, sein Portfolio um weitere Futures auf, so dass es
am Tagesende insgesamt
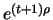 Futures enthält. Der am
Tag
Futures enthält. Der am
Tag  eingenommene Betrag hat auf den Fälligkeitstermin
aufgezinst den Wert:
eingenommene Betrag hat auf den Fälligkeitstermin
aufgezinst den Wert:
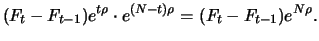 |
(4.10) |
Am Ende der Laufzeit ist der Future-Kontrakt durch den laufenden Gewinn-Verlust-Ausgleich bereits erfüllt
und verursacht keine weiteren Kosten. Die gesamten während der Laufzeit angefallenen Gewinne oder Kosten sind
aufgezinst auf den Tag 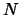 :
:
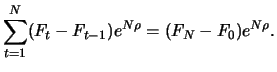 |
(4.11) |
Zusammen mit dem Zerobond hat Portfolio  daher zur Zeit
daher zur Zeit 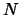 den Wert
da am Ende der Laufzeit Future-Preis
den Wert
da am Ende der Laufzeit Future-Preis 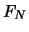 und aktueller Kurs
und aktueller Kurs
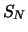 offensichtlich zusammenfallen.
offensichtlich zusammenfallen.
Beide Portfolios haben also am Tag 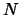 denselben Wert und somit
wegen der Arbitragefreiheit auch am Tag 0. Da der
Forward-Kontrakt mit Terminkurs
denselben Wert und somit
wegen der Arbitragefreiheit auch am Tag 0. Da der
Forward-Kontrakt mit Terminkurs 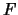 am Tag 0 wegen der
Definition des Forward-Preises den Wert 0 hat, ist der Wert von
Portfolio
am Tag 0 wegen der
Definition des Forward-Preises den Wert 0 hat, ist der Wert von
Portfolio  gleich dem Wert des Zerobonds, d.h.
gleich dem Wert des Zerobonds, d.h. 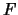 (Nominalwert
(Nominalwert
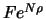 abgezinst auf den Tag 0). Entsprechend haben auch
die am Ende von Tag 0 in Portfolio
abgezinst auf den Tag 0). Entsprechend haben auch
die am Ende von Tag 0 in Portfolio  enthaltenen
enthaltenen 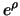 Futures wegen der Definition des Future-Preises den Wert 0, so
dass auch hier nur der Zerobond zum Portfoliowert beiträgt. Er
hat entsprechend den Wert
Futures wegen der Definition des Future-Preises den Wert 0, so
dass auch hier nur der Zerobond zum Portfoliowert beiträgt. Er
hat entsprechend den Wert 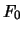 (
(
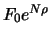 abgezinst auf den
Tag 0). Insgesamt schließen wir
abgezinst auf den
Tag 0). Insgesamt schließen wir 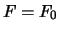 .
. 
Wir wollen nun mit ähnlichen Methoden Beziehungen zwischen den Preisen für Optionen
herleiten. Die elementarsten Eigenschaften fassen wir in der folgenden Bemerkung
ohne Beweis zusammen. Dazu benötigen wir den Begriff des inneren Wertes (intrinsic value).
Definition 4.1 (Innerer Wert)
Der
innere Wert einer Kaufoption zum
Zeitpunkt

ist gegeben durch
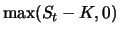
, der einer
Verkaufsoption durch
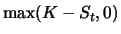
. Ist der innere Wert einer
Option positiv, so sagen wir, dass sie
im Geld ist. Ist
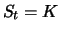
, so ist die Option
am Geld;
andernfalls ist die Option
aus dem Geld.
Bemerkung 4.1
Für Optionen gelten folgende elementare Beziehungen.
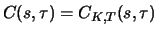
und
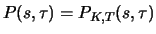
bezeichnen dabei den Wert zur Zeit

eines Calls bzw. Puts mit Ausübungskurs

und Verfallszeitpunkt

, wenn
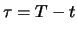
die Restlaufzeit ist und der Kurs des zugrundeliegenden
Finanzinstruments den Wert
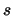
hat:
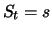
.
- Optionspreise sind nicht-negativ, da eine Ausübung nur
stattfindet, wenn es im Interesse des Optionshalters liegt. Eine Option gewährt Rechte ohne Pflichten.
- Zum Verfallszeitpunkt
 besitzen amerikanische und
europäische Optionen den gleichen Wert, da sie dann dem Besitzer identische Rechte einräumen. Zum Verfallszeitpunkt
besitzen amerikanische und
europäische Optionen den gleichen Wert, da sie dann dem Besitzer identische Rechte einräumen. Zum Verfallszeitpunkt  stimmen der Wert der Option und der innere Wert überein:
stimmen der Wert der Option und der innere Wert überein:
- Eine amerikanische Option muss mindestens zu ihrem
inneren Wert gehandelt werden, da andernfalls durch Kauf einer Option und augenblickliche Ausübung
Arbitrage möglich wäre. Diese Relation gilt für europäische Optionen im allgemeinen nicht.
Grund hierfür ist, dass eine europäische Option nur indirekt über ein Termingeschäft zum heutigen
Zeitpunkt vorzeitig ausgeübt werden kann. Der hierbei auftretende Abzinsungsfaktor kann den Wert
unter den inneren Wert der Option drücken.
- Der Wert zweier amerikanischer Optionen, die sich nur in
den Laufzeiten unterscheiden (Verfallszeitpunkte
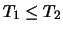 ), ist monoton in den Laufzeiten:
Dies folgt - zum Beispiel für Calls - unter Ausnutzung von 2. und 3. aus der zur Zeit
), ist monoton in den Laufzeiten:
Dies folgt - zum Beispiel für Calls - unter Ausnutzung von 2. und 3. aus der zur Zeit 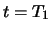 gültigen Ungleichung mit
gültigen Ungleichung mit
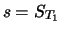
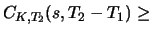 innerer Wert innerer Wert 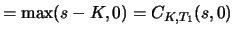 |
(4.12) |
Wegen der Arbitragefreiheit muss die Ungleichung auch zu jedem Zeitpunkt
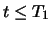 gelten. Für europäische Optionen ist diese Aussage im allgemeinen nicht erfüllt.
gelten. Für europäische Optionen ist diese Aussage im allgemeinen nicht erfüllt.
- Eine amerikanische Option hat mindestens den gleichen
Wert wie die ansonsten identische europäische Option, da die amerikanische Option dem Besitzer mehr Rechte einräumt.
- Der Wert eines Calls ist als Funktion des
Ausübungskurses monoton fallend, da das Kaufrecht umso wertvoller ist, je niedriger der vereinbarte Kaufpreis.
Entsprechend ist der Wert eines Puts als Funktion des Ausübungskurses monoton wachsend:
für
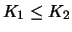 . Dies gilt für amerikanische und europäische Optionen.
. Dies gilt für amerikanische und europäische Optionen.
Der Wert einer europäischen Kauf- und Verkaufsoption auf das
gleiche Objekt mit gleicher Laufzeit und gleichem Ausübungskurs
sind direkt miteinander verbunden, ohne dass die Annahme eines
detaillierten mathematischen Modells nötig ist.
Satz 4.3 (Put-Call-Parität
für europäische Optionen)
Für den Wert eine europäischen Calls und eines europäischen Puts mit gleichem
Verfallszeitpunkt

, gleichem Ausübungskurs

auf dasselbe zugrundeliegende Finanzinstrument
gelten folgende Aussagen, wobei
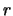
den stetigen Zinssatz bezeichnet:
- Fallen während der Restlaufzeit
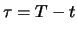 der Optionen Erträge
mit dem auf den Zeitpunkt
der Optionen Erträge
mit dem auf den Zeitpunkt  abgezinsten Gesamtbarwert
abgezinsten Gesamtbarwert 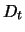 an, so ist
an, so ist
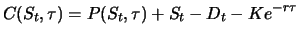 |
(4.13) |
 SFMPutCall.xpl
SFMPutCall.xpl
- Fallen während der Restlaufzeit
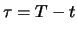 der Optionen stetige Bestandshaltekosten mit Rate
der Optionen stetige Bestandshaltekosten mit Rate
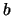 auf das Objekt an, so ist
auf das Objekt an, so ist
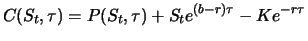 |
(4.14) |
Beweis:
Zur Vereinfachung der Sprechweise nehmen wir wieder speziell an,
dass das Objekt eine Aktie ist. Wir betrachten ein Portfolio  ,
das nur aus einem Call besteht, und duplizieren es durch ein
geeignetes Portfolio
,
das nur aus einem Call besteht, und duplizieren es durch ein
geeignetes Portfolio  , das unter anderem einen Put enthält.
, das unter anderem einen Put enthält.
1. Im Fall diskreter Dividenden betrachten wir folgendes Portfolio  zum Zeitpunkt
zum Zeitpunkt  :
:
- Kaufe den Put.
- Verkaufe einen Zerobond mit Nominalwert
 , fällig zum Zeitpunkt
, fällig zum Zeitpunkt  .
.
- Kaufe eine Aktie.
- Verkaufe einen Zerobond zum (aktuellen) Wert
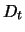 .
.
Da das Portfolio eine Aktie enthält, wirft es Dividenden ab, deren Wert abgezinst auf den
Zeitpunkt  gerade
gerade 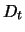 ist. Diese Erträge werden am Ende der Laufzeit benutzt, um die Anleihe in Position d)
zurückzuzahlen, so dass der Wert dieser Position zu 0 wird. Tabelle 2.1 zeigt nun den Wert
des Portfolios
ist. Diese Erträge werden am Ende der Laufzeit benutzt, um die Anleihe in Position d)
zurückzuzahlen, so dass der Wert dieser Position zu 0 wird. Tabelle 2.1 zeigt nun den Wert
des Portfolios  zum Zeitpunkt
zum Zeitpunkt  abhängig davon, ob der Put ausgeübt wird (
abhängig davon, ob der Put ausgeübt wird (
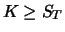 ) oder nicht.
) oder nicht.
Tabelle 2.1:
Wert von Portfolio  zum Zeitpunkt
zum Zeitpunkt  (Satz 2.3)
(Satz 2.3)
| |
Wert zum Zeitpunkt  |
| Position |
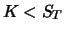 |
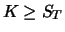 |
| a) |
0 |
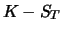 |
| b) |
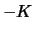 |
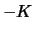 |
| c) |
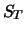 |
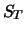 |
| d) |
0 |
0 |
| Summe |
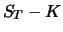 |
0 |
|
Zur Zeit  hat Portfolio
hat Portfolio  damit denselben Wert
damit denselben Wert
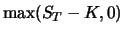 wie der Call.
Um Arbitragemöglichkeiten zu verhindern, müssen daher beide Portfolios auch
zum Zeitpunkt
wie der Call.
Um Arbitragemöglichkeiten zu verhindern, müssen daher beide Portfolios auch
zum Zeitpunkt  denselben Wert haben, d.h. es gilt
denselben Wert haben, d.h. es gilt
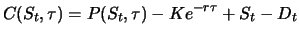 |
(4.15) |
2. Für den Fall einer Aktie mit stetiger Dividendenrendite 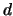 und entsprechenden Bestandshaltekosten
und entsprechenden Bestandshaltekosten 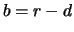 betrachten wir
dasselbe Portfolio
betrachten wir
dasselbe Portfolio  wie in Teil 1., jedoch ohne die Position
d). Stattdessen werden in Position c)
wie in Teil 1., jedoch ohne die Position
d). Stattdessen werden in Position c)
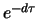 Aktien anstelle
von einer Aktie gekauft, deren Dividenden direkt wieder in die
gleiche Aktie reinvestiert werden. Bei negativem
Aktien anstelle
von einer Aktie gekauft, deren Dividenden direkt wieder in die
gleiche Aktie reinvestiert werden. Bei negativem 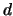 werden die
auftretenden Kosten durch Verkäufe des Objektes finanziert.
Hierdurch enthält Portfolio
werden die
auftretenden Kosten durch Verkäufe des Objektes finanziert.
Hierdurch enthält Portfolio  zum Zeitpunkt
zum Zeitpunkt  genau eine
Aktie, und man kann wie in Teil 1. schließen, dass der Wert
des Portfolios
genau eine
Aktie, und man kann wie in Teil 1. schließen, dass der Wert
des Portfolios  zum Zeitpunkt
zum Zeitpunkt  gleich dem Wert des Calls
ist.
gleich dem Wert des Calls
ist. 
Der Beweis der Put-Call-Parität funktioniert nur für
europäische Optionen. Für amerikanische Optionen kann es
vorkommen, dass Put oder Call vorzeitig ausgeübt wird und die
beiden Portfolios gar nicht bis zum Ende der Laufzeit gehalten
werden.
Das folgende Resultat bietet eine Möglichkeit zur Überprüfung der Konsistenz von Optionspreisen
auf dasselbe Objekt. Ist die hier formulierte Konvexität verletzt, ist Arbitrage möglich, wie wir in dem
sich anschließenden Beispiel zeigen.
Satz 4.4
Der Preis einer (amerikanischen oder europäischen) Option ist als Funktion des Ausübungskurses konvex.
Beweis:
Es genügt Calls zu betrachten. Für Puts läuft der Beweis
analog; für europäische Optionen folgt dies direkt aus der
Put-Call-Parität, da dort der explizit von  abhängige Term
linear in
abhängige Term
linear in  ist.
ist.
Für
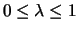 und
und 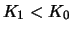 definieren wir
definieren wir
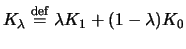 . Wir betrachten ein
Portfolio
. Wir betrachten ein
Portfolio  , das zur Zeit
, das zur Zeit 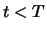 aus einem Call mit
Ausübungskurs
aus einem Call mit
Ausübungskurs 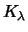 und Fälligkeitszeitpunkt
und Fälligkeitszeitpunkt  besteht. Wir duplizieren dieses Portfolio durch folgendes
Portfolio
besteht. Wir duplizieren dieses Portfolio durch folgendes
Portfolio  zum Zeitpunkt
zum Zeitpunkt  :
:
- Kaufe
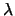 Calls mit Ausübungskurs
Calls mit Ausübungskurs 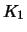 , Fälligkeit
, Fälligkeit  .
.
- Kaufe
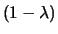 Calls mit Ausübungskurs
Calls mit Ausübungskurs 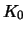 , Fälligkeit
, Fälligkeit  .
.
Liquidieren wir das Portfolio zu einem beliebigen Zeitpunkt
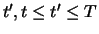 , so lässt sich die Differenz der Werte
der Portfolios
, so lässt sich die Differenz der Werte
der Portfolios  und
und  zu diesem Zeitpunkt in der Tabelle 2.2 ablesen.
zu diesem Zeitpunkt in der Tabelle 2.2 ablesen.
Tabelle 2.2:
Wertdifferenz der Portfolios  und
und  zum Zeitpunkt
zum Zeitpunkt 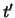 (Satz 2.4)
(Satz 2.4)
|
|
Wert zum Zeitpunkt 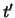 |
|
Position |
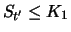 |
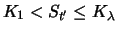 |
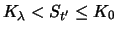 |
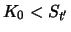 |
 1. 1. |
0 |
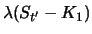 |
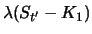 |
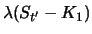 |
 2. 2. |
0 |
0 |
0 |
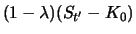 |
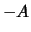 |
0 |
0 |
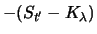 |
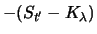 |
|
Summe |
0 |
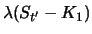 |
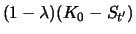 |
0 |
|
Da in der letzten Zeile der Tabelle jeweils
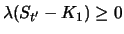 und
und
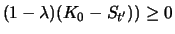 gilt, ist
die Differenz der Werte von Portfolio
gilt, ist
die Differenz der Werte von Portfolio  und Portfolio
und Portfolio  zum
Zeitpunkt
zum
Zeitpunkt 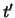 und damit wegen der Arbitragefreiheit auch zum
Zeitpunkt
und damit wegen der Arbitragefreiheit auch zum
Zeitpunkt 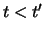 größer gleich Null. Es gilt also mit
größer gleich Null. Es gilt also mit
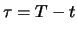
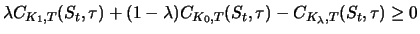 |
(4.16) |

Wir haben bereits angemerkt, dass Optionen monotone Funktionen des
Ausübungskurses sind. Der folgende Satz liefert für
europäische Optionen eine schärfere Aussage.
Satz 4.5
Für zwei europäische Calls (bzw. Puts) mit gleichem
Verfallsdatum

und den Ausübungskursen
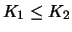
gilt zur Zeit
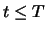
:
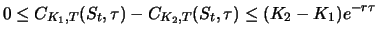 |
(4.18) |
mit Restlaufzeit
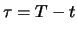
und Zinssatz
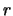
bzw.
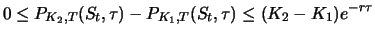 |
(4.19) |
Sind die Call- bzw. Putwerte als Funktion des Ausübungskurses differenzierbar, folgt durch Grenzübergang
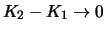
auch
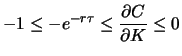 bzw. bzw.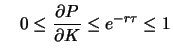 |
(4.20) |
Beweis:
Wir führen den Beweis für Calls; für Puts ist die Argumentation analog. Hierzu betrachten wir ein Portfolio  ,
das nur einen Call mit Ausübungskurs
,
das nur einen Call mit Ausübungskurs 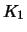 enthält, und vergleichen es mit einem Duplikationsportfolio
enthält, und vergleichen es mit einem Duplikationsportfolio  ,
das zum Zeitpunkt
,
das zum Zeitpunkt  aus den beiden folgenden Positionen besteht:
aus den beiden folgenden Positionen besteht:
- Kaufe einen Call mit Ausübungskurs
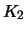 .
.
- Kaufe einen Zerobond mit Nominalwert
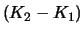 , fällig zum Zeitpunkt
, fällig zum Zeitpunkt  .
.
Die Differenz der Werte der Portfolios  und
und  zum Zeitpunkt
zum Zeitpunkt  lässt sich in der Tabelle
2.5 ablesen.
lässt sich in der Tabelle
2.5 ablesen.
Tabelle:
Wertdifferenz der Portfolios  und
und  zum Zeitpunkt
zum Zeitpunkt  (Satz 2.5)
(Satz 2.5)
| |
Wert zum Zeitpunkt  |
| Position |
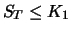 |
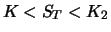 |
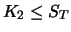 |
 1. 1. |
0 |
0 |
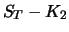 |
 2. 2. |
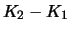 |
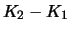 |
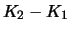 |
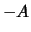 |
0 |
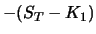 |
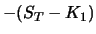 |
| Summe |
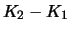 |
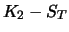 |
0 |
|
Der Wert von Portfolio  zum Zeitpunkt
zum Zeitpunkt  ist offensichtlich mindestens so groß wie der Wert von
Portfolio
ist offensichtlich mindestens so groß wie der Wert von
Portfolio  . Folglich muss dies wegen der Arbitragefreiheit auch für den Zeitpunkt
. Folglich muss dies wegen der Arbitragefreiheit auch für den Zeitpunkt  gelten und wir
schließen:
gelten und wir
schließen:

![]() denselben Wert haben, auch zu jedem früheren Zeitpunkt
denselben Wert haben, auch zu jedem früheren Zeitpunkt ![]() wertgleich sind.
Wegen ihrer Bedeutung stellen wir diese Argumentation hier in ihren Einzelheiten vor.
Wir gehen von zwei Portfolios
wertgleich sind.
Wegen ihrer Bedeutung stellen wir diese Argumentation hier in ihren Einzelheiten vor.
Wir gehen von zwei Portfolios ![]() und
und ![]() , die sich aus beliebigen Anlageformen zusammensetzen, aus. Ihr Wert
zur Zeit
, die sich aus beliebigen Anlageformen zusammensetzen, aus. Ihr Wert
zur Zeit ![]() bezeichnen wir mit
bezeichnen wir mit ![]() bzw.
bzw. ![]() . Wir nehmen für einen festen Zeitpunkt
. Wir nehmen für einen festen Zeitpunkt ![]() an, dass
sicher
an, dass
sicher
![]() unabhängig von der Wertentwicklung der einzelnen, in
unabhängig von der Wertentwicklung der einzelnen, in ![]() und
und ![]() enthaltenen Anlagen.
Für einen beliebigen früheren Zeitpunkt
enthaltenen Anlagen.
Für einen beliebigen früheren Zeitpunkt ![]() nehmen wir ohne Beschränkung der Allgemeinheit an,
dass
nehmen wir ohne Beschränkung der Allgemeinheit an,
dass
![]() . Ein Investor kann zur Zeit
. Ein Investor kann zur Zeit ![]() ohne Eigenkapitaleinsatz ein kombiniertes Portfolio
aufbauen, indem er eine Einheit aller Anlagen in
ohne Eigenkapitaleinsatz ein kombiniertes Portfolio
aufbauen, indem er eine Einheit aller Anlagen in ![]() kauft, eine Einheit aller Anlagen in
kauft, eine Einheit aller Anlagen in ![]() verkauft (Short-selling)
und den Differenzbetrag
verkauft (Short-selling)
und den Differenzbetrag
![]() festverzinslich zum Zinssatz
festverzinslich zum Zinssatz ![]() anlegt. Das kombinierte
Portfolio hat zur Zeit
anlegt. Das kombinierte
Portfolio hat zur Zeit ![]() den Wert
den Wert
![]() zusammengestellt, dass neben Anlagen mit bekanntem Preis auch eine Einheit des
Derivats enthält. Diesem Portfolio wird ein zweites, sogenanntes Duplikationsportfolio
zusammengestellt, dass neben Anlagen mit bekanntem Preis auch eine Einheit des
Derivats enthält. Diesem Portfolio wird ein zweites, sogenanntes Duplikationsportfolio
![]() gegenübergestellt, das ausschließlich aus Anlagen mit bekanntem Preis
besteht und so konstruiert worden ist, dass es zu einem festen Zeitpunkt
gegenübergestellt, das ausschließlich aus Anlagen mit bekanntem Preis
besteht und so konstruiert worden ist, dass es zu einem festen Zeitpunkt ![]() sicher denselben Wert wie
sicher denselben Wert wie ![]() hat.
Dann folgt aus der Arbitragefreiheit, dass beide Portfolios zu jedem früheren Zeitpunkt wertgleich sind, und daraus
ergibt sich sofort der Wert des Finanzderivats zu jedem Zeitpunkt
hat.
Dann folgt aus der Arbitragefreiheit, dass beide Portfolios zu jedem früheren Zeitpunkt wertgleich sind, und daraus
ergibt sich sofort der Wert des Finanzderivats zu jedem Zeitpunkt ![]() . Wir illustrieren diese Vorgehensweise
am Beispiel eines Terminkontrakts.
. Wir illustrieren diese Vorgehensweise
am Beispiel eines Terminkontrakts.
![]() zwei Portfolios
zwei Portfolios ![]() und
und ![]() , die folgendes Aussehen haben:
, die folgendes Aussehen haben:
![]() , kann ähnlich argumentiert
werden. Wieder betrachten wir zwei Portfolios
, kann ähnlich argumentiert
werden. Wieder betrachten wir zwei Portfolios ![]() und
und ![]() zum Zeitpunkt
zum Zeitpunkt ![]() ,
wobei
,
wobei ![]() wie im ersten Teil des Beweises gewählt wird. Portfolio
wie im ersten Teil des Beweises gewählt wird. Portfolio ![]() hat folgendes
Aussehen
hat folgendes
Aussehen
![]() -ten Tages, wird in Portfolio
-ten Tages, wird in Portfolio
![]() der Ertrag
der Ertrag
![]() des Zerobonds benutzt, um den
Terminkontrakt zu erfüllen und
des Zerobonds benutzt, um den
Terminkontrakt zu erfüllen und ![]() Aktien zum Preis von
jeweils
Aktien zum Preis von
jeweils ![]() zu kaufen. Das Portfolio
zu kaufen. Das Portfolio ![]() enthält dann nur noch
diese Aktien und hat den Wert
enthält dann nur noch
diese Aktien und hat den Wert
![]() . Wir zeigen nun, dass
dies auch für Portfolio
. Wir zeigen nun, dass
dies auch für Portfolio ![]() gilt.
gilt.
![]() sind
sind ![]() Futures im Portfolio, und
der Halter erhält durch den Gewinn-Verlust-Ausgleich den Betrag
Futures im Portfolio, und
der Halter erhält durch den Gewinn-Verlust-Ausgleich den Betrag
![]() , der auch negativ sein kann. Während
des Tages stockt er kostenfrei, da mit dem aktuellen Future-Preis
als Terminkurs, sein Portfolio um weitere Futures auf, so dass es
am Tagesende insgesamt
, der auch negativ sein kann. Während
des Tages stockt er kostenfrei, da mit dem aktuellen Future-Preis
als Terminkurs, sein Portfolio um weitere Futures auf, so dass es
am Tagesende insgesamt
![]() Futures enthält. Der am
Tag
Futures enthält. Der am
Tag ![]() eingenommene Betrag hat auf den Fälligkeitstermin
aufgezinst den Wert:
eingenommene Betrag hat auf den Fälligkeitstermin
aufgezinst den Wert:
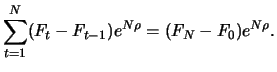
![]() denselben Wert und somit
wegen der Arbitragefreiheit auch am Tag 0. Da der
Forward-Kontrakt mit Terminkurs
denselben Wert und somit
wegen der Arbitragefreiheit auch am Tag 0. Da der
Forward-Kontrakt mit Terminkurs ![]() am Tag 0 wegen der
Definition des Forward-Preises den Wert 0 hat, ist der Wert von
Portfolio
am Tag 0 wegen der
Definition des Forward-Preises den Wert 0 hat, ist der Wert von
Portfolio ![]() gleich dem Wert des Zerobonds, d.h.
gleich dem Wert des Zerobonds, d.h. ![]() (Nominalwert
(Nominalwert
![]() abgezinst auf den Tag 0). Entsprechend haben auch
die am Ende von Tag 0 in Portfolio
abgezinst auf den Tag 0). Entsprechend haben auch
die am Ende von Tag 0 in Portfolio ![]() enthaltenen
enthaltenen ![]() Futures wegen der Definition des Future-Preises den Wert 0, so
dass auch hier nur der Zerobond zum Portfoliowert beiträgt. Er
hat entsprechend den Wert
Futures wegen der Definition des Future-Preises den Wert 0, so
dass auch hier nur der Zerobond zum Portfoliowert beiträgt. Er
hat entsprechend den Wert ![]() (
(
![]() abgezinst auf den
Tag 0). Insgesamt schließen wir
abgezinst auf den
Tag 0). Insgesamt schließen wir ![]() .
. ![]()
![]() zum Zeitpunkt
zum Zeitpunkt ![]() :
:
![]() und
und ![]() definieren wir
definieren wir
![]() . Wir betrachten ein
Portfolio
. Wir betrachten ein
Portfolio ![]() , das zur Zeit
, das zur Zeit ![]() aus einem Call mit
Ausübungskurs
aus einem Call mit
Ausübungskurs ![]() und Fälligkeitszeitpunkt
und Fälligkeitszeitpunkt ![]() besteht. Wir duplizieren dieses Portfolio durch folgendes
Portfolio
besteht. Wir duplizieren dieses Portfolio durch folgendes
Portfolio ![]() zum Zeitpunkt
zum Zeitpunkt ![]() :
:
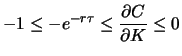 bzw.
bzw.