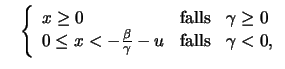Als erstes betrachten wir das stochastische Verhalten des
Maximums
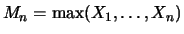 von
von 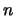 unabhängigen, identisch verteilten Zufallsgrößen
unabhängigen, identisch verteilten Zufallsgrößen
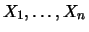 mit Verteilungsfunktion
mit Verteilungsfunktion 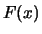 . Bei Anwendungen im
Risikomanagement ist
. Bei Anwendungen im
Risikomanagement ist
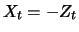 die negativen Renditen am Tag
die negativen Renditen am Tag
 . Die Verteilungsfunktion von
. Die Verteilungsfunktion von 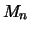 ist
ist
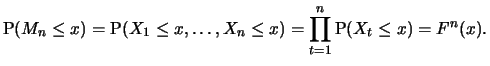 |
(19.1) |
Wir betrachten nur unbeschränkte Zufallsgrößen 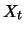 , d.h.
, d.h.
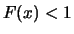 für alle
für alle
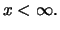 Dann gilt offensichtlich
Dann gilt offensichtlich
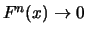 für alle
für alle 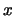 , wenn
, wenn
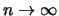 , und damit
, und damit
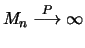 . Das Maximum von
. Das Maximum von 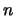 unbeschränkten Zufallsgrößen wächst also über alle Grenzen.
Um ein nichtdegeneriertes Grenzverhalten zu bekommen, müssen wir
unbeschränkten Zufallsgrößen wächst also über alle Grenzen.
Um ein nichtdegeneriertes Grenzverhalten zu bekommen, müssen wir
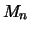 in geeigneter Weise standardisieren.
in geeigneter Weise standardisieren.
Definition 19.1 (Maximumsanziehungsbereich)
Die Zufallsgrößen
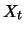
gehören zum
Maximumsanziehungsbereich (maximum domain of attraction, MDA)
einer nicht-degenerierten Verteilung
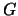
, wenn für geeignete
Zahlenfolgen
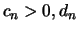
gilt:
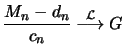
für
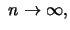
d.h.
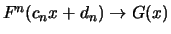
für alle Stetigkeitspunkte
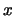
der Verteilungsfunktion
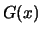
.
Es stellt sich heraus, dass nur sehr wenige Verteilungen  als
Grenzverteilungen des standardisierten Maximums
als
Grenzverteilungen des standardisierten Maximums  in Frage
kommen. Diese werden Extremwertverteilungen genannt. Es
handelt sich dabei um die folgenden drei Typen von
Verteilungsfunktionen:
in Frage
kommen. Diese werden Extremwertverteilungen genannt. Es
handelt sich dabei um die folgenden drei Typen von
Verteilungsfunktionen:
| Fréchet: |
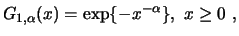 für ein für ein
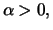 |
| |
|
| Gumbel: |
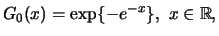 |
| |
|
| Weibull: |
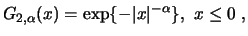 für ein für ein
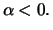 |
Abb.:
Fréchet (Rot)-, Gumbel (Schwarz)- und Weibull-Verteilungen (Blau).
 SFMevt1.xpl
SFMevt1.xpl
|
|
Die Fréchet-Verteilungen sind auf den nichtnegativen Zahlen
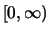 konzentriert, die Weibull-Verteilungen dagegen auf
konzentriert, die Weibull-Verteilungen dagegen auf
![$ (- \infty, 0],$](sfmimg3360.gif) während Gumbel-verteilte Zufallsgrößen
beliebige reelle Werte annehmen können. Abbildung 17.1
zeigt die Wahrscheinlichkeitsdichten der Gumbelverteilung, der
Fréchet-Verteilung mit Parameter
während Gumbel-verteilte Zufallsgrößen
beliebige reelle Werte annehmen können. Abbildung 17.1
zeigt die Wahrscheinlichkeitsdichten der Gumbelverteilung, der
Fréchet-Verteilung mit Parameter 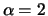 und der
Weibull-Verteilung mit Parameter
und der
Weibull-Verteilung mit Parameter 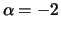 , Wir können alle
drei Verteilungstypen in der einheitlichen von Mises-Form
darstellen:
, Wir können alle
drei Verteilungstypen in der einheitlichen von Mises-Form
darstellen:
Definition 19.2 (Extremwertverteilungen)
Die
allgemeine Extremwertverteilung
(GEV =
generalized extreme value) mit
Formparameter
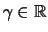
hat die Verteilungsfunktion:
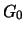 ist die Gumbelverteilung, während
ist die Gumbelverteilung, während
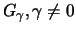 über die folgenden Beziehungen mit den
Fréchet- und
Weibull-Verteilungen verknüpft sind:
über die folgenden Beziehungen mit den
Fréchet- und
Weibull-Verteilungen verknüpft sind:
Die Definition beschreibt die Standardform der
GEV-Verteilungen. Im allgemeinen können
wir das Zentrum und die Skala ändern, um andere GEV-Verteilungen
zu bekommen:
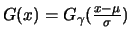 mit dem
Formparameter
mit dem
Formparameter 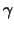 , dem Lageparameter
, dem Lageparameter
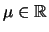 und dem Skalenparameter
und dem Skalenparameter
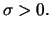 Für die asymptotische Theorie spielt dies keine Rolle, da
die standardisierenden Folgen
Für die asymptotische Theorie spielt dies keine Rolle, da
die standardisierenden Folgen 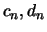 stets so gewählt werden
können, dass die Grenzverteilung
stets so gewählt werden
können, dass die Grenzverteilung 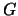 die Standardform (
die Standardform (
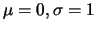 ) hat. Die entscheidende Aussage über das
Grenzverhalten des Maximums
) hat. Die entscheidende Aussage über das
Grenzverhalten des Maximums 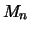 ist das Fisher-Tippett-Theorem:
ist das Fisher-Tippett-Theorem:
Satz 19.1
Wenn es Folgen
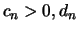
und eine nichtdegenerierte
Verteilung
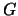
gibt, so dass
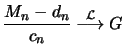
für
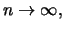
dann ist
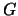
eine GEV-Verteilung.
Beweis:
Zum besseren Verständnis skizzieren wir die wesentlichen
Beweisideen für dieses zentrale Resultat. Sei 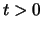 , und
bezeichne
, und
bezeichne ![$ [ z ]$](sfmimg3382.gif) den ganzzahligen Anteil von
den ganzzahligen Anteil von 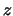 . Da
. Da ![$ F^ {[nt]}$](sfmimg3383.gif) die Verteilungsfunktion von
die Verteilungsfunktion von ![$ M_{[nt]}$](sfmimg3384.gif) ist, gilt wegen unserer
Annahme an das asymptotische Verhalten von
ist, gilt wegen unserer
Annahme an das asymptotische Verhalten von 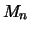 speziell
Auf der anderen
Seite gilt auch
speziell
Auf der anderen
Seite gilt auch
![$\displaystyle F^ {[nt]} (c_n x + d_n) = \{ F^ n (c_n x + d_n) \} ^ {\frac{[nt]}{n}}
\longrightarrow G^ t (x)\ $](sfmimg3388.gif)
für
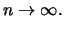
Anders ausgedrückt heißt dies
für
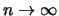 . Aufgrund des im Anschluss an die
Beweisskizze formulierten Lemmas ist dies nur möglich, wenn
und
. Aufgrund des im Anschluss an die
Beweisskizze formulierten Lemmas ist dies nur möglich, wenn
und
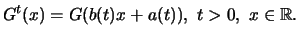 |
(19.2) |
Diese Beziehungen gelten für beliebige Werte  . Wir benutzen
sie speziell für beliebige
. Wir benutzen
sie speziell für beliebige 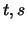 und
und 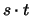 und erhalten
und erhalten
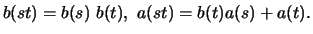 |
(19.3) |
Die Funktionalgleichungen (17.2), (17.3)
für
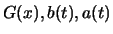 besitzen nur eine Lösung,
wenn
besitzen nur eine Lösung,
wenn 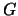 eine der Verteilungen
eine der Verteilungen
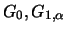 oder
oder
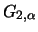 ist, d.h.
ist, d.h. 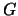 muss eine GEV-Verteilung sein.
muss eine GEV-Verteilung sein.

Lemma 19.1 (Konvergenztypen-Theorem)
Seien
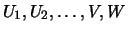
Zufallsvariablen,
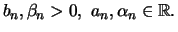
Wenn
in Verteilung für
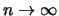
, dann gilt:
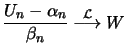
genau dann, wenn
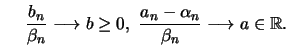
In diesem Fall hat
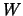
dieselbe Verteilung wie
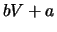
.
Wir bemerken, dass die GEV-Verteilungen identisch mit den
sogenannten max-stabilen Verteilungen sind, bei denen für alle 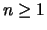 das Maximum
das Maximum
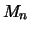 von
von 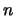 u.i.v. Zufallsvariablen
u.i.v. Zufallsvariablen
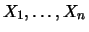 dieselbe
Verteilung wie
dieselbe
Verteilung wie
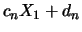 für passend gewählte
für passend gewählte
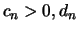 hat.
hat.
Abb.:
Wahrscheinlichkeitsplot für die Normalverteilung
von pseudo Zufallsvariablen mit Extremwertverteilung, und zwar
Fréchet (Ober-links), Weibull (Ober-rechts) und Gumbel (Unterteil).
 SFMevt2.xpl
SFMevt2.xpl
|
|
Abbildung 17.2 zeigt den sogenannten Normalplot, d.h. den
Wahrscheinlichkeitsplot (PP-plot) für die Normalverteilung, vgl.
Abschnitt 17.2 für den Spezialfall
 ,
für auf dem Rechner erzeugte Zufallsgrößen mit einer
Gumbel-Verteilung, Fréchet-Verteilung mit Parameter
,
für auf dem Rechner erzeugte Zufallsgrößen mit einer
Gumbel-Verteilung, Fréchet-Verteilung mit Parameter
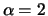 bzw. Weibull-Verteilung mit Parameter
bzw. Weibull-Verteilung mit Parameter 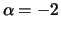 . Die
Unterschiede zu normalverteilten Zufallsgrößen, für die der
Normalplot ungefähr eine Gerade zeigt, sind deutlich sichtbar.
. Die
Unterschiede zu normalverteilten Zufallsgrößen, für die der
Normalplot ungefähr eine Gerade zeigt, sind deutlich sichtbar.
Wenn das Maximum von u.i.v. Zufallsgrößen nach geeigneter
Standardisierung in Verteilung konvergiert, stellt sich die Frage,
welche der drei Typen von GEV-Verteilungen als Grenzverteilung
auftritt. Dabei ist entscheidend, wie schnell die
Wahrscheinlichkeit für extrem große Beobachtungen oberhalb einer
Schwelle 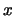 abklingt, wenn
abklingt, wenn 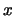 wächst. Da diese
Überschreitungswahrscheinlichkeiten
in der Extremwerttheorie eine wichtige Rolle spielen, führen wir
für sie eine eigene Notation ein:
wächst. Da diese
Überschreitungswahrscheinlichkeiten
in der Extremwerttheorie eine wichtige Rolle spielen, führen wir
für sie eine eigene Notation ein:
Der Zusammenhang zwischen den
Überschreitungswahrscheinlichkeiten
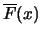 und der
Verteilung der Maxima
und der
Verteilung der Maxima 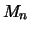 wird durch das folgende Resultat
deutlich.
wird durch das folgende Resultat
deutlich.
Satz 19.2
a) Für
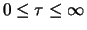
und jede Folge reeller Zahlen
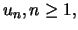
gilt für
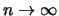
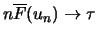
genau dann, wenn
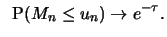
b)
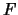
gehört genau dann zum
Maximumsanziehungsbereich der GEV-Verteilung
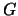
mit den
standardisierenden Folgen
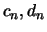
, wenn für
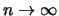
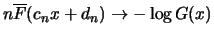
für alle
Die Überschreitungswahrscheinlichkeiten der
Fréchet-Verteilung
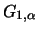 verhalten sich für
verhalten sich für
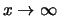 wie
wie
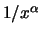 , da die Exponentialfunktion um 0 herum
approximativ linear ist, d.h.
, da die Exponentialfunktion um 0 herum
approximativ linear ist, d.h.
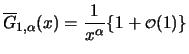
für
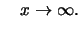
Im wesentlichen zeigen alle Verteilungen, die zum
Maximumsanziehungsbereich dieser Fréchet-Verteilung gehören,
das gleiche Verhalten;
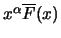 ist für
ist für
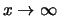 beinahe konstant, d.h. genauer: eine langsam variierende
Funktion.
beinahe konstant, d.h. genauer: eine langsam variierende
Funktion.
Definition 19.3
Eine positive messbare Funktion
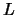
auf
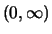
heißt
langsam variierend, wenn für alle
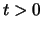
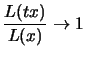
für
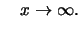
Typische langsam variierende Funktionen sind neben den Konstanten
solche mit logarithmischem Wachstum, zum Beispiel
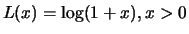 .
.
Satz 19.3
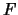
gehört genau dann zum Maximumsanziehungsbereich der
Fréchet-Verteilung
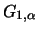
für ein
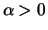
, wenn
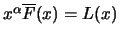
eine langsam variierende
Funktion ist. Die Zufallsgrößen
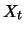
mit der
Verteilungsfunktion
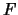
sind unbeschränkt, d.h.
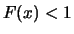
für
alle
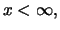
und es gilt
mit
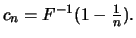
Für die Beschreibung der standardisierenden Folge 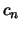 haben wir
die im folgenden eingeführte Notation benutzt.
haben wir
die im folgenden eingeführte Notation benutzt. 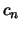 ist ein
extremes Quantil der Verteilung
ist ein
extremes Quantil der Verteilung 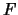 , und es gilt
, und es gilt
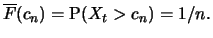
Definition 19.4 (Quantilenfunktion)
Ist
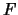
eine Verteilungsfunktion, so
nennen wir die verallgemeinerte Inverse
die
Quantilenfunktion. Es gilt dann
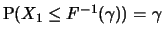
, d.h.
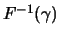
ist das
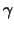
-
Quantil der Verteilung
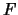
.
Wenn
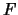
streng monoton wächst und stetig ist, dann ist
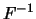
die übliche Inverse von
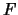
.
Es gibt ein entsprechendes Kriterium für Weibull-Verteilungen,
das durch Ausnutzung der Beziehung
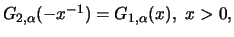 gezeigt werden kann. Zufallsgrößen,
deren Maxima im Grenzfall Weibull-verteilt sind, sind allerdings
auf jeden Fall beschränkt, d.h. es gibt eine Konstante
gezeigt werden kann. Zufallsgrößen,
deren Maxima im Grenzfall Weibull-verteilt sind, sind allerdings
auf jeden Fall beschränkt, d.h. es gibt eine Konstante
 , so dass
, so dass 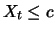 mit Wahrscheinlichkeit 1. Daher sind
sie für Finanzanwendungen nur in speziellen Situationen
interessant, wo z.B. durch eine Art Rückversicherungsstrategie
der Verlust, der aus einer Investition entstehen kann, begrenzt
worden ist. Um regelmäßige Fallunterscheidungen zu vermeiden,
diskutieren wir im folgenden meist nur den Fall, dass die Verluste
unbeschränkt sind. Der Fall von Verlusten, die eine bekannte
Schranke nicht überschreiten können, kann in ähnlicher Weise
behandelt werden.
mit Wahrscheinlichkeit 1. Daher sind
sie für Finanzanwendungen nur in speziellen Situationen
interessant, wo z.B. durch eine Art Rückversicherungsstrategie
der Verlust, der aus einer Investition entstehen kann, begrenzt
worden ist. Um regelmäßige Fallunterscheidungen zu vermeiden,
diskutieren wir im folgenden meist nur den Fall, dass die Verluste
unbeschränkt sind. Der Fall von Verlusten, die eine bekannte
Schranke nicht überschreiten können, kann in ähnlicher Weise
behandelt werden.
Die Fréchet-Verteilungen treten als Grenzverteilungen der
Maxima von Zufallsgrößen auf, für die die Wahrscheinlichkeit
von großen Werten oberhalb von 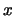 nur langsam mit
nur langsam mit 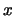 abfällt,
während nur beschränkte Zufallsgrößen zum
Maximumsanziehungsbereich von Weibull-Verteilungen gehören. Viele
bekannte Verteilungen wie die Exponential- oder Normalverteilung
gehören weder zu der einen noch zu der anderen Gruppe. Es liegt
die Vermutung nahe, dass in diesen Fällen die Verteilung der
geeignet standardisierten Maxima gegen die Gumbel-Verteilung
konvergiert. Die allgemeinen Bedingungen hierfür sind allerdings
komplizierter und schwerer überprüfbar als für die
Fréchet-Verteilungen.
abfällt,
während nur beschränkte Zufallsgrößen zum
Maximumsanziehungsbereich von Weibull-Verteilungen gehören. Viele
bekannte Verteilungen wie die Exponential- oder Normalverteilung
gehören weder zu der einen noch zu der anderen Gruppe. Es liegt
die Vermutung nahe, dass in diesen Fällen die Verteilung der
geeignet standardisierten Maxima gegen die Gumbel-Verteilung
konvergiert. Die allgemeinen Bedingungen hierfür sind allerdings
komplizierter und schwerer überprüfbar als für die
Fréchet-Verteilungen.
Satz 19.4
Die Verteilungsfunktion
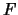
unbeschränkter Zufallsgrößen
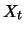
gehört genau dann zum Maximumsanziehungsbereich der
Gumbel-Verteilung, wenn messbare Skalierungsfunktionen
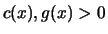
sowie eine absolut stetige Funktion
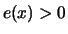
existieren mit
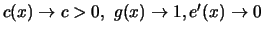
für
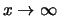
so dass für ein
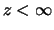
:
In diesem Fall gilt
mit
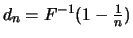
und
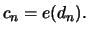
Als Funktion 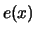 kann die mittlere
Exzess-Funktion
gewählt werden, die im folgenden noch eingehender betrachtet
wird.
kann die mittlere
Exzess-Funktion
gewählt werden, die im folgenden noch eingehender betrachtet
wird.
Die Exponentialverteilung mit Parameter 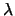 hat die
Verteilungsfunktion
hat die
Verteilungsfunktion
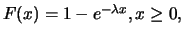 so
dass
so
dass
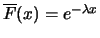 die Bedingungen des
Satzes mit
die Bedingungen des
Satzes mit
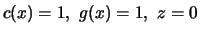 und
und
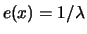 erfüllt. Das Maximum
erfüllt. Das Maximum 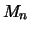 von
von 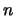 unabhängigen exponentiell
verteilten Zufallsgrößen mit Parameter
unabhängigen exponentiell
verteilten Zufallsgrößen mit Parameter 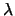 konvergiert
daher in Verteilung gegen die Gumbel-Verteilung:
konvergiert
daher in Verteilung gegen die Gumbel-Verteilung:
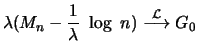
für
Im allgemeinen sind die Bedingungen aber nicht so leicht zu
überprüfen. Es gibt allerdings einfachere hinreichende
Kriterien, mit denen sich zum Beispiel zeigen lässt, dass auch
die Normalverteilung zum Maximumsanziehungsbereich der
Gumbel-Verteilung gehört. Ist zum Beispiel 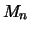 das Maximum von
das Maximum von
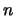 unabhängigen standardnormalverteilten Zufallsgrößen, so
gilt
unabhängigen standardnormalverteilten Zufallsgrößen, so
gilt
 SFMevtex1.xpl
SFMevtex1.xpl
Zu den Verteilungen im Maximumsanziehungsbereich der
Fréchet-Verteilung
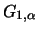 gehört insbesondere die
Pareto-Verteilung mit
Verteilungsfunktion
gehört insbesondere die
Pareto-Verteilung mit
Verteilungsfunktion
sowie alle anderen Verteilungen mit Paretoflanken, d.h. mit
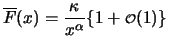
für
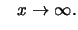
Da hier
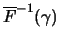 für
für
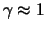 sich
wie
sich
wie
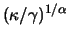 verhält, stimmt
verhält, stimmt 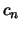 für
für
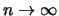 mit
mit
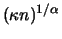 überein, und
überein, und
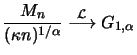
für
Es besteht ein enger Zusammenhang zwischen dem Grenzverhalten der
Maxima von Zufallsgrößen und der Verteilung der entsprechenden
Exzesse, die die Grundlage eines wichtigen Schätzverfahrens in
der Extremwertstatistik bilden und im nächsten Abschnitt
definiert werden. Es handelt sich dabei im wesentlichen um die
Überschreitungen der Beobachtungen über einen vorgegebenen
Schwellenwert 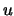 . Ihre Verteilung
. Ihre Verteilung 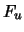 wird folgendermaßen
definiert:
wird folgendermaßen
definiert:
Definition 19.5 (Exzessverteilung)
Sei
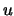
ein beliebiger
Schwellenwert und
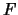
die Verteilungsfunktion einer
unbeschränkten Zufallsgröße
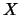
.
- a)
-
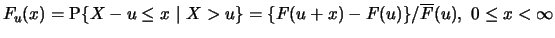 heißt die
Exzess-Verteilungsfunktion über dem Schwellenwert
heißt die
Exzess-Verteilungsfunktion über dem Schwellenwert 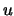 .
.
- b)
-
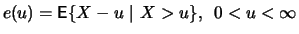 ,
ist die
mittlere Exzess-Funktion.
,
ist die
mittlere Exzess-Funktion.
Mit partieller Integration folgt, dass diese Definition der
mittleren Exzess-Funktion mit der in Anschluss an Satz
17.4 gegebenen übereinstimmt:
Ist 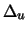 eine Zufallsgröße mit der Verteilungsfunktion
eine Zufallsgröße mit der Verteilungsfunktion
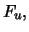 dann ist ihr Erwartungswert
dann ist ihr Erwartungswert
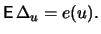
Satz 19.5
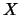
sei eine positive, unbeschränkte Zufallsgröße mit absolut
stetiger
Verteilungsfunktion
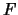
.
a) Die mittlere Exzess-Funktion
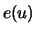
bestimmt
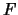
eindeutig:
b) Wenn
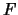
im
Maximumsanziehungsbereich der Fréchet-Verteilung
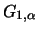
liegt,
so ist
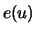
für
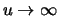
näherungsweise linear:
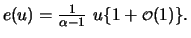
Definition 19.6 (Pareto-Verteilungen)
Die
allgemeine Pareto-Verteilung
(GP =
generalized Pareto) mit den Parametern
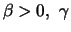
besitzt die Verteilungsfunktion
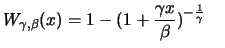
für
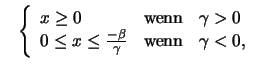
und
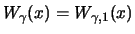
heißen
allgemeine
Standard-Pareto-Verteilungen oder
standardisierte
GP-Verteilungen.
Abb.:
Standard-Pareto-Verteilungen (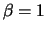 ) mit den Parametern
) mit den Parametern
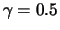 (Rot),
0 (Schwarz) und
(Rot),
0 (Schwarz) und 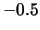 (Blau).
(Blau).
 SFMgpdist.xpl
SFMgpdist.xpl
|
|
Abbildung 17.3 zeigt die allgemeinen
Standard-Pareto-Verteilungen mit den Parametern
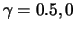 und
und 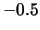 .
.
Für
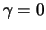 ist die standardisierte GP-Verteilung eine Exponentialverteilung mit Parameter
ist die standardisierte GP-Verteilung eine Exponentialverteilung mit Parameter 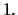 Für
Für
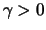 ist sie eine Pareto-Verteilung
ist sie eine Pareto-Verteilung
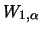 mit
dem Parameter
mit
dem Parameter
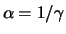 . Für
. Für
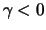 heißt die
GP-Verteilung auch eine Beta-Verteilung und hat die
Verteilungsfunktion
heißt die
GP-Verteilung auch eine Beta-Verteilung und hat die
Verteilungsfunktion
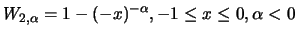 .
.
Satz 19.6
Die Verteilung
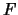
liegt genau dann im MDA der GEV-Verteilung
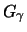
mit dem Formparameter
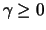
, wenn für eine
messbare Funktion
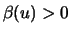
und die allgemeine
Pareto-Verteilung
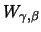
gilt:
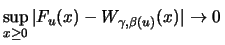
für
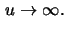
Ein entsprechendes Resultat gilt auch für den Fall 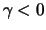 ,
wobei das Supremum über diejenigen
,
wobei das Supremum über diejenigen 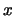 genommen werden muss, für
die
genommen werden muss, für
die
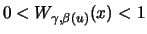 .
.
Für die allgemeine Pareto-Verteilung
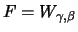 gilt schon für jeden endlichen Schwellenwert
gilt schon für jeden endlichen Schwellenwert 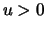
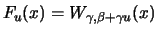
für
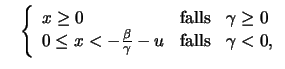
In diesem Fall ist also
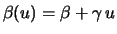 .
.
![]() von
von ![]() unabhängigen, identisch verteilten Zufallsgrößen
unabhängigen, identisch verteilten Zufallsgrößen
![]() mit Verteilungsfunktion
mit Verteilungsfunktion ![]() . Bei Anwendungen im
Risikomanagement ist
. Bei Anwendungen im
Risikomanagement ist
![]() die negativen Renditen am Tag
die negativen Renditen am Tag
![]() . Die Verteilungsfunktion von
. Die Verteilungsfunktion von ![]() ist
ist
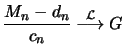 für
für ![]() ist die Gumbelverteilung, während
ist die Gumbelverteilung, während
![]() über die folgenden Beziehungen mit den
Fréchet- und
Weibull-Verteilungen verknüpft sind:
über die folgenden Beziehungen mit den
Fréchet- und
Weibull-Verteilungen verknüpft sind:
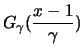
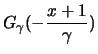
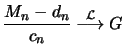 für
für ![$\displaystyle \frac{M_{[nt]} - d_{[nt]}}{c_{[nt]}} \stackrel{{\cal L}}{\longrig...
...\ \, \quad \frac{M_{[nt]} - d_n}{c_n} \stackrel{{\cal L}}{\longrightarrow} G^ t$](sfmimg3389.gif)
![$\displaystyle \frac{c_n}{c_{[nt]}} \longrightarrow b(t) \ge 0,\
\quad \frac{d_n - d_{[nt]}}{c_{[nt]}} \longrightarrow a(t) $](sfmimg3390.gif)
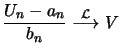
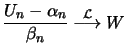 genau dann, wenn
genau dann, wenn 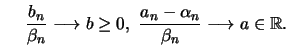
![]() das Maximum
das Maximum
![]() von
von ![]() u.i.v. Zufallsvariablen
u.i.v. Zufallsvariablen
![]() dieselbe
Verteilung wie
dieselbe
Verteilung wie
![]() für passend gewählte
für passend gewählte
![]() hat.
hat.
![\includegraphics[width=0.4\defpicwidth]{evt21.ps}](sfmimg3406.gif)
![\includegraphics[width=0.4\defpicwidth]{evt22.ps}](sfmimg3407.gif)
![\includegraphics[width=0.4\defpicwidth]{evt23.ps}](sfmimg3408.gif)
![]() abklingt, wenn
abklingt, wenn ![]() wächst. Da diese
Überschreitungswahrscheinlichkeiten
in der Extremwerttheorie eine wichtige Rolle spielen, führen wir
für sie eine eigene Notation ein:
wächst. Da diese
Überschreitungswahrscheinlichkeiten
in der Extremwerttheorie eine wichtige Rolle spielen, führen wir
für sie eine eigene Notation ein:
![]() verhalten sich für
verhalten sich für
![]() wie
wie
![]() , da die Exponentialfunktion um 0 herum
approximativ linear ist, d.h.
, da die Exponentialfunktion um 0 herum
approximativ linear ist, d.h.
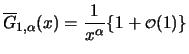 für
für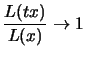 für
für![]() .
.
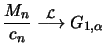
![]() gezeigt werden kann. Zufallsgrößen,
deren Maxima im Grenzfall Weibull-verteilt sind, sind allerdings
auf jeden Fall beschränkt, d.h. es gibt eine Konstante
gezeigt werden kann. Zufallsgrößen,
deren Maxima im Grenzfall Weibull-verteilt sind, sind allerdings
auf jeden Fall beschränkt, d.h. es gibt eine Konstante
![]() , so dass
, so dass ![]() mit Wahrscheinlichkeit 1. Daher sind
sie für Finanzanwendungen nur in speziellen Situationen
interessant, wo z.B. durch eine Art Rückversicherungsstrategie
der Verlust, der aus einer Investition entstehen kann, begrenzt
worden ist. Um regelmäßige Fallunterscheidungen zu vermeiden,
diskutieren wir im folgenden meist nur den Fall, dass die Verluste
unbeschränkt sind. Der Fall von Verlusten, die eine bekannte
Schranke nicht überschreiten können, kann in ähnlicher Weise
behandelt werden.
mit Wahrscheinlichkeit 1. Daher sind
sie für Finanzanwendungen nur in speziellen Situationen
interessant, wo z.B. durch eine Art Rückversicherungsstrategie
der Verlust, der aus einer Investition entstehen kann, begrenzt
worden ist. Um regelmäßige Fallunterscheidungen zu vermeiden,
diskutieren wir im folgenden meist nur den Fall, dass die Verluste
unbeschränkt sind. Der Fall von Verlusten, die eine bekannte
Schranke nicht überschreiten können, kann in ähnlicher Weise
behandelt werden.
![]() nur langsam mit
nur langsam mit ![]() abfällt,
während nur beschränkte Zufallsgrößen zum
Maximumsanziehungsbereich von Weibull-Verteilungen gehören. Viele
bekannte Verteilungen wie die Exponential- oder Normalverteilung
gehören weder zu der einen noch zu der anderen Gruppe. Es liegt
die Vermutung nahe, dass in diesen Fällen die Verteilung der
geeignet standardisierten Maxima gegen die Gumbel-Verteilung
konvergiert. Die allgemeinen Bedingungen hierfür sind allerdings
komplizierter und schwerer überprüfbar als für die
Fréchet-Verteilungen.
abfällt,
während nur beschränkte Zufallsgrößen zum
Maximumsanziehungsbereich von Weibull-Verteilungen gehören. Viele
bekannte Verteilungen wie die Exponential- oder Normalverteilung
gehören weder zu der einen noch zu der anderen Gruppe. Es liegt
die Vermutung nahe, dass in diesen Fällen die Verteilung der
geeignet standardisierten Maxima gegen die Gumbel-Verteilung
konvergiert. Die allgemeinen Bedingungen hierfür sind allerdings
komplizierter und schwerer überprüfbar als für die
Fréchet-Verteilungen.
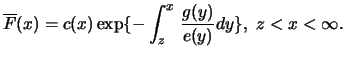
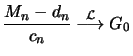
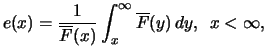
![]() hat die
Verteilungsfunktion
hat die
Verteilungsfunktion
![]() so
dass
so
dass
![]() die Bedingungen des
Satzes mit
die Bedingungen des
Satzes mit
![]() und
und
![]() erfüllt. Das Maximum
erfüllt. Das Maximum ![]() von
von ![]() unabhängigen exponentiell
verteilten Zufallsgrößen mit Parameter
unabhängigen exponentiell
verteilten Zufallsgrößen mit Parameter ![]() konvergiert
daher in Verteilung gegen die Gumbel-Verteilung:
konvergiert
daher in Verteilung gegen die Gumbel-Verteilung:
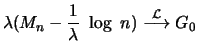 für
für![]() das Maximum von
das Maximum von
![]() unabhängigen standardnormalverteilten Zufallsgrößen, so
gilt
unabhängigen standardnormalverteilten Zufallsgrößen, so
gilt
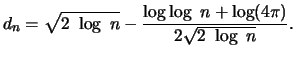
![]() gehört insbesondere die
Pareto-Verteilung mit
Verteilungsfunktion
gehört insbesondere die
Pareto-Verteilung mit
Verteilungsfunktion
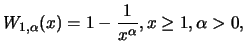
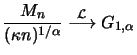 für
für ![]() . Ihre Verteilung
. Ihre Verteilung ![]() wird folgendermaßen
definiert:
wird folgendermaßen
definiert:
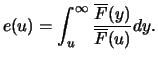
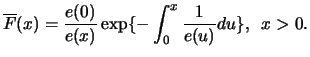
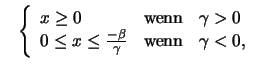
![\includegraphics[width=1\defpicwidth]{gpdist.ps}](sfmimg3486.gif)
![]() ist die standardisierte GP-Verteilung eine Exponentialverteilung mit Parameter
ist die standardisierte GP-Verteilung eine Exponentialverteilung mit Parameter ![]() Für
Für
![]() ist sie eine Pareto-Verteilung
ist sie eine Pareto-Verteilung
![]() mit
dem Parameter
mit
dem Parameter
![]() . Für
. Für
![]() heißt die
GP-Verteilung auch eine Beta-Verteilung und hat die
Verteilungsfunktion
heißt die
GP-Verteilung auch eine Beta-Verteilung und hat die
Verteilungsfunktion
![]() .
.
![]() gilt schon für jeden endlichen Schwellenwert
gilt schon für jeden endlichen Schwellenwert ![]()