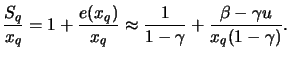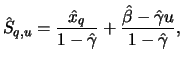Sei
a) Der Value-at-Risk (VaR)
ist das ![]() -Quantil
-Quantil
Der Value-at-Risk, den wir bereits in den vorhergehenden Kapiteln betrachtet haben, ist nicht das einzige Maß, mit dem sich Marktrisiken quantifizieren lassen. In diesem Abschnitt betrachten wir zusätzlich eine Alternative und einige prinzipielle Forderungen an Risikomaße. Außerdem diskutieren wir Schätzer für diese Maße für den Fall, dass mit extrem hohen Verlusten zu rechnen ist.
a) Der Value-at-Risk (VaR)
ist das ![]() -Quantil
-Quantil
| (A1) |
(Monotonie) |
| (A2)
|
(Subadditivität) |
| (A3)
|
(positive Homogeneität) |
| (A4)
|
(Translationequivarianz) |
Der VaR verletzt in gewissen Situationen Bedingung (A2). ![]() seien z.B. u.i.v., und beide nehmen nur die beiden Werte 0 oder
100 an mit den Wahrscheinlichkeiten
seien z.B. u.i.v., und beide nehmen nur die beiden Werte 0 oder
100 an mit den Wahrscheinlichkeiten
![]() und
und
![]() Dann nimmt
Dann nimmt ![]() die Werte 0, 100
und 200 an mit
die Werte 0, 100
und 200 an mit
![]() ,
,
![]() und
und
![]() Für
Für
![]() und
und
![]() ,
z.B. für
,
z.B. für
![]() , gilt daher
, gilt daher
Der erwartete Shortfall ist dagegen ein kohärentes Risikomaß,
das immer alle vier Bedingungen erfüllt. Er liefert auch intuitiv
mehr Einsicht in das tatsächliche Risiko extremer Verluste als
der Value-at-Risk. Der VaR hängt nur von der Häufigkeit von
Verlusten oberhalb des ![]() -Quantils
-Quantils ![]() ab, sagt aber nichts
darüber aus, ob diese Verluste die Schwelle
ab, sagt aber nichts
darüber aus, ob diese Verluste die Schwelle ![]() stets nur
geringfügig überschreitet oder ob auch mit Verlusten, die viel
größer als
stets nur
geringfügig überschreitet oder ob auch mit Verlusten, die viel
größer als ![]() sind, gerechnet werden muss. Der erwartete
Shortfall ist dagegen der Erwartungswert der Verluste jenseits von
sind, gerechnet werden muss. Der erwartete
Shortfall ist dagegen der Erwartungswert der Verluste jenseits von
![]() und hängt von deren tatsächlichen Größe ab.
und hängt von deren tatsächlichen Größe ab.
Der Value-at-Risk ist einfach ein Quantil und kann zum Beispiel
als Stichprobenquantil
![]() geschätzt werden,
wobei
geschätzt werden,
wobei
![]() die empirische Verteilungsfunktion einer
Stichprobe von negativen Erträgen, d.h. Verlusten, aus der
Vergangenheit ist. Wie zu Beginn dieses Kapitels diskutiert, ist
dieser Schätzer für
die empirische Verteilungsfunktion einer
Stichprobe von negativen Erträgen, d.h. Verlusten, aus der
Vergangenheit ist. Wie zu Beginn dieses Kapitels diskutiert, ist
dieser Schätzer für
![]() , also gerade für die
typischen VaR-Niveaus 0.95 und 0.99, oft zu optimistisch.
Alternative VaR-Schätzer, die die Möglichkeit extremer Verluste
besser berücksichtigen, sind der POT- oder der
Hill-Quantilenschätzer.
, also gerade für die
typischen VaR-Niveaus 0.95 und 0.99, oft zu optimistisch.
Alternative VaR-Schätzer, die die Möglichkeit extremer Verluste
besser berücksichtigen, sind der POT- oder der
Hill-Quantilenschätzer.
Analoge Schätzer für den erwarteten Shortfall lassen sich leicht
herleiten. Dieses Risikomaß hängt eng mit der mittleren
Exzessfunktion an der Stelle ![]() zusammen, wie sofort aus
den Definitionen folgt:
zusammen, wie sofort aus
den Definitionen folgt:
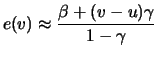 für
für