In order to derive confidence intervals or confidence bands for
![]() we have to know its sampling distribution. The
distribution for finite sample sizes is not known but the
following result concerning the asymptotic distribution of
we have to know its sampling distribution. The
distribution for finite sample sizes is not known but the
following result concerning the asymptotic distribution of
![]() can be derived. Suppose that
can be derived. Suppose that ![]() exists and
exists and
![]() . Then
. Then
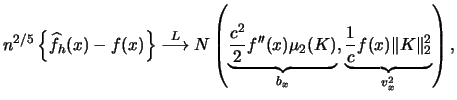 |
(3.49) |
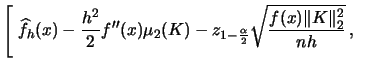 |
(3.50) | ||
![$\displaystyle \quad\quad
\widehat{f}_{h}(x)-\frac{h^{2}}{2}f''(x)\mu_{2}(K)
+z_{1-\frac{\alpha}{2}}\sqrt{\frac{f(x)\Vert K
\Vert _{2}^{2}}{nh}}\;\Bigg].$](spmhtmlimg811.gif) |
![$\displaystyle \left[\;\widehat{f}_{h}(x)-z_{1-\frac{\alpha}{2}}\sqrt{\frac{\wid...
...alpha}{2}} \sqrt{\frac{\widehat{f}_{h}(x)\Vert K \Vert _{2}^{2}}{nh}}\;\right].$](spmhtmlimg813.gif) |
(3.51) |
Note that this is a confidence interval for ![]() and not the entire
density
and not the entire
density ![]() . Confidence bands for
. Confidence bands for ![]() have only been derived under
some rather restrictive assumptions.
Suppose that
have only been derived under
some rather restrictive assumptions.
Suppose that ![]() is a density on
is a density on ![]() and given that certain regularity
conditions are satisfied then for
and given that certain regularity
conditions are satisfied then for
![]() ,
,
![]() , and for all
, and for all
![]() the following
formula has been derived by
Bickel & Rosenblatt (1973)
the following
formula has been derived by
Bickel & Rosenblatt (1973)
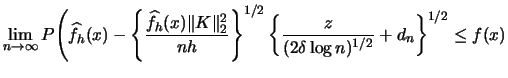 | |||
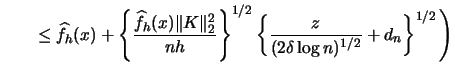 |
|||
| (3.52) | |||
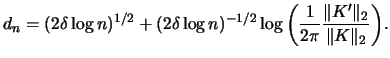
When using nonparametric density estimators in practice, another important question arises: Can we find a parametric estimate that describes the data in a sufficiently satisfactory manner? That is, given a specific sample, could we justify the use of a parametric density function? Note that using parametric estimates is computationally far less intensive. Moreover, many important properties, e.g. the moments and derivatives, of parametric density functions are usually well known so they can easily be manipulated for analytical purposes. To verify whether a parametric density function describes the data accurately enough in a statistical sense, we can make use of confidence bands.
![\includegraphics[width=1.2\defpicwidth]{SPMcps85distA.ps}](spmhtmlimg826.gif)
|
Now, as with many size distributions, the nonparametric density estimate closely resembles the lognormal distribution. Thus, we calculated the estimated parameters of the lognormal distribution,
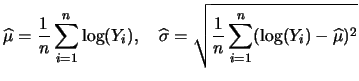
Note that the nonparametrically estimated density is considerably flatter than its parametric counterpart. Now, let us see whether the sample provides some justification for using the lognormal density. To this end, we computed the 95% confidence bands around our nonparametric estimate, as shown in Figure 3.9.
![\includegraphics[width=1.2\defpicwidth]{SPMcps85distB.ps}](spmhtmlimg829.gif)
|
We found that in the neighborhood of the mode, the parametric density exceeds the upper limit of the confidence band. Hence, in a strict sense the data reject the lognormal distribution as the ``true" distribution of average hourly earnings (at the 5% level). Yet, it is quite obvious from the picture that the lognormal density captures the shape of the nonparametrically estimated density quite well. Hence, if all we are interested in are qualitative features of the underlying distribution like skewness or unimodality the lognormal distribution seems to work sufficiently well.
Let us remark that checking whether the parametric density estimate does not exceed the confidence bands is a very conservative test for its correct specification. In contrast to fully parametric approaches, it is often possible to find a nonparametric test yielding better rates of convergence than the nonparametric density estimate. Moreover, there exist more powerful model checks than looking at confidence bands. Therefore, as nonparametric testing is an exhaustive topic on its own, we will not discuss nonparametric tests in detail in this book. Instead, we restrict ourselves to the presentation of the main ideas and for further details refer to the bibliographic notes.
![\includegraphics[width=1.2\defpicwidth]{SPMcps85distC.ps}](spmhtmlimg830.gif)
|
In the problem considered in the preceeding paragraph, we were concerned
with how well the lognormal distribution works as an estimate of the
true density for the entire range of possible values of average
hourly earnings. This global check of the adequacy of the lognormal
was provided by comparing it with confidence bands around the
nonparametrically estimated density.
Suppose that instead we are merely interested in how well the
lognormal fits at a single given value of average hourly
earnings. Then, the proper comparison confronts the lognormal density
at this point with a confidence interval around the
nonparametric estimate. As confidence intervals, by construction,
only refer to a single point, they are narrower (at this point) than a
confidence band which is supposed to hold simultaneously at many
points.
Figure 3.10 shows both the asymptotic confidence bands (solid
line) and the asymptotic confidence intervals (broken line) of our kernel
estimate. Both are computed for the same 95% significance level.
Note that, as expected, the confidence intervals are narrower
than the confidence bands.