1.2 Regression

Let us now consider a typical linear regression problem. We assume that anyone of you has been exposed to the linear regression model where the mean of a dependent variable $Y$ is related to a set of explanatory variables $X_1,X_2,\ldots,X_d$ in the following way:

$$E(Y\vert{\boldsymbol{X}}) = X_{1}\beta_{1}+\ldots+X_{d}\beta_{d}={\boldsymbol{X}}^\top{\boldsymbol{\beta}}.$$ (1.1)

Here $E(Y\vert{\boldsymbol{X}})$ denotes the expectation conditional on the vector ${\boldsymbol{X}}=(X_{1}$, $X_2$, $\ldots$, $X_{d})^\top$ and $\beta_j,$ $j=1,2,\ldots,d$ are unknown coefficients. Defining $\varepsilon$ as the deviation of $Y$ from the conditional mean $E(Y\vert{\boldsymbol{X}})$:

$$\varepsilon= Y-E(Y\vert{\boldsymbol{X}})$$ (1.2)

we can write

$$Y ={\boldsymbol{X}}^\top{\boldsymbol{\beta}}+\varepsilon.$$ (1.3)

EXAMPLE 1.2  
To take a specific example, let $Y$ be log wages and consider the explanatory variables schooling (measured in years), labor market experience (measured as $\textrm{AGE}-\textrm{SCHOOL}-6$) and experience squared. If we assume that, on average, log wages are linearly related to these explanatory variables then the linear regression model applies:

$$E(Y\vert\textrm{SCHOOL},\textrm{EXP}) = \beta_{0}+\beta_{1}\cdotp\textrm{SCHOOL}+\beta_2\cdotp\textrm{EXP}+\beta_3\cdotp\textrm{EXP}^2.$$ (1.4)

Note that we have included an intercept ($\beta_0$) in the model. $\Box$

The model of equation (1.4) has played an important role in empirical labor economics and is often called human capital earnings equation (or Mincer earnings equation to honor Jacob Mincer, a pioneer of this line of research). From the perspective of this course, an important characteristic of equation (1.4) is its parametric form: the shape of the regression function is governed by the unknown parameters $\beta_j,$ $j=1,2,\ldots,d$. That is, all we have to do in order to determine the linear regression function (1.4) is to estimate the unknown parameters $\beta_j$. On the other hand, the parametric regression function of equation (1.4) a priori rules out many conceivable nonlinear relationships between $Y$ and ${\boldsymbol{X}}$.

Let $m(\textrm{SCHOOL},\textrm{EXP})$ be the true, unknown regression function of log wages on schooling and experience. That is,

$$E(Y\vert\textrm{SCHOOL},\textrm{EXP}) = m(\textrm{SCHOOL},\textrm{EXP}).$$ (1.5)

Suppose that you were assigned the following task: estimate the regression of log wages on schooling and experience as accurately as possible in one trial. That is, you are not allowed to change your model if you find that the initial specification does not fit the data well. Of course, you could just go ahead and assume, as we have done above, that the regression you are supposed to estimate has the form specified in (1.4). That is, you assume that

$$m(\textrm{SCHOOL},\textrm{EXP})= \beta_{1}+\beta_{2}\cdotp\textrm{SCHOOL} +\beta_3\cdotp\textrm{EXP}+\beta_4\cdotp \textrm{EXP}^2,$$

and estimate the unknown parameters by the method of ordinary least squares, for example. But maybe you would not fit this parametric model if we told you that there are ways of estimating the regression function without having to make any prior assumptions about its functional form (except that it is a smooth function). Remember that you have just one trial and if the form of $m(\textrm{SCHOOL},\textrm{EXP})$ is very different from (1.4) then estimating the parametric model may give you very inaccurate results.

It turns out that there are indeed ways of estimating $m(\bullet)$ that merely assume that $m(\bullet)$ is a smooth function. These methods are called nonparametric regression estimators and part of this course will be devoted to studying nonparametric regression.

Nonparametric regression estimators are very flexible but their statistical precision decreases greatly if we include several explanatory variables in the model. The latter caveat has been appropriately termed the curse of dimensionality. Consequently, researchers have tried to develop models and estimators which offer more flexibility than standard parametric regression but overcome the curse of dimensionality by employing some form of dimension reduction. Such methods usually combine features of parametric and nonparametric techniques. As a consequence, they are usually referred to as semiparametric methods. Further advantages of semiparametric methods are the possible inclusion of categorical variables (which can often only be included in a parametric way), an easy (economic) interpretation of the results, and the possibility of a part specification of a model.

In the following three sections we use the earnings equation and other examples to illustrate the distinctions between parametric, nonparametric and semiparametric regression and we certainly hope that this will whet your appetite for the material covered in this course.

1.2.1 Parametric Regression

Versions of the human capital earnings equation of (1.4) have probably been estimated by more researchers than any other model of empirical economics. For a detailed nontechnical and well-written discussion see Berndt (1991, Chapter 5). Here, we want to point out that:

• Under certain simplifying assumptions, $\beta_2$ accurately measures the rate of return to schooling.
• Human capital theory suggests a concave wage-experience profile: rapid human capital accumulation in the early stage of one's labor market career, with rising wages that peak somewhere during midlife and decline thereafter as hours worked and the incentive to invest in human capital decrease. This is the reason for including both $\textrm{EXP}$ and $\textrm{EXP}^2$ in the model. In order to get a profile as the one envisaged by theory, the estimated value of $\beta_3$ should be positive and that of $\beta_4$ should be negative.

Table 1.1: Results from OLS estimation for Example 1.2

Dependent Variable: Log Wages
Variable	Coefficients	S.E.	$t$-values
$\textrm{SCHOOL}$	0.0898	0.0083	10.788
$\textrm{EXP}$	0.0349	0.0056	6.185
$\textrm{EXP}^2$	-0.0005	0.0001	-4.307
constant	0.5202	0.1236	4.209
$R^2=0.24$, sample size $n = 534$

We have estimated the coefficients of (1.4) using ordinary least squares (OLS), using a subsample of the 1985 Current Population Survey (CPS) provided by Berndt (1991). The results are given in Table 1.1.

Figure 1.2: Wage-schooling and wage-experience profile
SPMcps85lin

The estimated rate of return to schooling is roughly $9\%$. Note that the estimated coefficients of $\textrm{EXP}$ and $\textrm{EXP}^2$ have the signs predicted by human capital theory. The shape of the wage-schooling (a plot of SCHOOL vs. $0.0898\cdotp\textrm{SCHOOL}$) and wage-experience (a plot of EXP vs. $0.0349 \cdotp\textrm{EXP}-0.0005 \cdotp\textrm{EXP}^2$) profiles are given in the left and right graphs of Figure 1.2, respectively.

The estimated wage-schooling relation is linear ``by default'' since we did not include $\textrm{SCHOOL}^2,$ say, to allow for some kind of curvature within the parametric framework. By looking at Figure 1.2 it is clear that the estimated coefficients of $\textrm{EXP}$ and $\textrm{EXP}^2$ imply the kind of concave wage-earnings profile predicted by human capital theory.

Figure 1.3: Parametrically estimated regression function
SPMcps85lin

We have also plotted a graph (Figure 1.3) of the estimated regression surface, i.e. a plot that has the values of the estimated regression function (obtained by evaluating $0.0898\cdotp\textrm{SCHOOL}+0.0349\cdotp\textrm{EXP} -0.0005\cdotp\textrm{EXP}^2$ at the observed combinations of schooling and experience) on the vertical axis and schooling and experience on the horizontal axes.

All of the element curves of the surface appear similar to Figure 1.2 (right) in the direction of experience and like Figure 1.2 (left) in the direction of schooling. To gain a better understanding of the three-dimensional picture we have plotted a single wage-experience profile in three dimensions, fixing schooling at 12 years. Hence, Figure 1.3 highlights the wage-earnings profile for high school graduates.

1.2.2 Nonparametric Regression

Suppose that we want to estimate

$$E(Y\vert\textrm{SCHOOL},\textrm{EXP}) = m(\textrm{SCHOOL},\textrm{EXP}).$$ (1.6)

and we are only willing to assume that $m(\bullet)$ is a smooth function. Nonparametric regression estimators produce an estimate of $m(\bullet)$ at an arbitrary point ( $\textrm{SCHOOL}=s,\textrm{EXP}=e$) by locally weighted averaging over log wages (here $s$ and $e$ denote two arbitrary values that SCHOOL and EXP may take on, such as 12 and 15). Locally weighting means that those values of log wages will be higher weighted for which the corresponding observations of EXP and SCHOOL are close to the point $(s,e)$. Let us illustrate this principle with an example. Let $s=8$ and $e=7$ and suppose you can use the four observations given in Table 1.2 to estimate $m(8,7)$:

Table 1.2: Example observations

Observation	log(WAGES)	SCHOOL	EXP
1	7.31	8	8
2	7.6	16	1
3	7.4	8	6
4	7.8	12	2

Figure 1.4: Nonparametrically estimated regression function
SPMcps85reg

In nonparametric regression $m(8,7)$ is estimated by averaging over the observed values of the dependent variable log wage. But not all values will be given the same weight. In our example, observation 1 will get the most weight since it has values of schooling and experience that are very close to the point where we want to estimate. This makes a lot of sense: if we want to estimate mean log wages for individuals with 8 years of schooling and 7 years of experience then the observed log wage of a person with 8 years of schooling and 8 years of experience seems to be much more informative than the observed log wage of a person with 12 years of schooling and 2 years of experience.

Consequently, any reasonable weighting scheme will give more weight to 7.31 than to 7.8 when we average over observed log wages. The exact method of weighting is determined by a weight function that makes precise the idea of weighting nearby observations more heavily. In fact, the weight function might be such that observations that are too far away get zero weight. In our example, observation 2 has values of experience and schooling that are so far away from 8 years of schooling and 7 years of experience that a weight function might assign zero value to the corresponding value of log wages (7.6). It is in this sense that the averaging is local. In Figure 1.4, the surface of nonparametrically estimated values of $m(\bullet)$ are shown. Here, a so-called kernel estimator has been used.

As long as we are dealing with only one regressor, the results of estimating a regression function nonparametrically can easily be displayed in a graph. The following example illustrates this. It relates net-income data, as we considered in Example 1.1, to a second variable that measures household expenditure.

EXAMPLE 1.3  
Consider for instance the dependence of food expenditure on net-income. Figure 1.5 shows the so-called Engel curve (after the German Economist Engel) of net-income and food share estimated using data from the 1973 Family Expenditure Survey of roughly 7000 British households. The figure supports the theory of Engel who postulated in 1857:

... je ärmer eine Familie ist, einen desto größeren Antheil von der Gesammtausgabe muß zur Beschaffung der Nahrung aufgewendet werden ... (The poorer a family, the bigger the share of total expenditure that has to be used for food.)

 $\Box$

Figure: Engel curve, U.K. Family Expenditure Survey 1973
SPMengelcurve2

1.2.3 Semiparametric Regression

To illustrate semiparametric regression let us return to the human capital earnings function of Example 1.2. Suppose the regression function of log wages on schooling and experience has the following shape:

$$E(Y\vert\textrm{SCHOOL},\textrm{EXP}) = \alpha+g_1(\textrm{SCHOOL}) +g_2(\textrm{EXP}).$$ (1.7)

Here $g_1(\bullet)$ and $g_2(\bullet)$ are two unknown, smooth functions and $\alpha$ is an unknown parameter. Note that this model combines the simple additive structure of the parametric regression model (referred to hereafter as the additive model) with the flexibility of the nonparametric approach. This is done by not imposing any strong shape restrictions on the functions that determine how schooling and experience influence the mean regression of log wages. The procedure employed to estimate this model will be explained in greater detail later in this course. It should be clear, however, that in order to estimate the unknown functions $g_1(\bullet)$ and $g_2(\bullet)$ nonparametric regression estimators have to be employed. That is, when estimating semiparametric models we usually have to use nonparametric techniques. Hence, we will have to spend a substantial amount of time studying nonparametric estimation if we want to understand how to estimate semiparametric models. For now, we want to focus on the results and compare them with the parametric fit.

Figure: Additive model fit vs. parametric fit, wage-schooling (left) and wage-experience (right)
SPMcps85add

In Figure 1.6 the parametrically estimated wage-schooling and wage-experience profiles are shown as thin lines whereas the estimates of $g_1(\bullet)$ and $g_2(\bullet)$ are displayed as thick lines with bullets. The parametrically estimated wage-school and wage-experience profiles show a good deal of similarity with the estimate of $g_1(\bullet)$ and $g_2(\bullet)$, except for the shape of the curve at extremal values. The good agreement between parametric estimates and additive model fit is also visible from the plot of the estimated regression surface, which is shown in Figure 1.7.

Figure 1.7: Surface plot for the additive model
SPMcps85add

Hence, we may conclude that in this specific example the parametric model is supported by the more flexible nonparametric and semiparametric methods. This potential usefulness of nonparametric and semiparametric techniques for checking the adequacy of parametric models will be illustrated in several other instances in the latter part of this course.

Take a closer look at (1.6) and (1.7). Observe that in (1.6) we have to estimate one unknown function of two variables whereas in (1.7) we have to estimate two unknown functions, each a function of one variable. It is in this sense that we have reduced the dimensionality of the estimation problem. Whereas all researchers might agree that additive models like the one in (1.7) are achieving a dimension reduction over completely nonparametric regression, they may not agree to call (1.7) a semiparametric model, as there are no parameters to estimate (except for the intercept parameter $\alpha$). In the following example we confront a standard parametric model with a more flexible model that, as you will see, truly deserves to be called semiparametric.

EXAMPLE 1.4  
In the earnings-function example, the dependent variable log wages can principally take on any positive value, i.e. the set of values $Y$ is infinite. This may not always be the case. For example, consider the decision of an East-German resident to move to Western Germany and denote the decision variable by $Y$. In this case, the dependent variable can take on only two values,

$$Y = \left\{ \begin{array}{ll} 1 & \quad \textrm{if the person can... ...e moving to the west,}\\ 0 & \quad \textrm{otherwise.} \\ \end{array} \right.$$

We will refer to this as a binary response later on. $\Box$

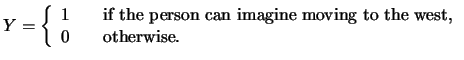
In Example 1.2 we tried to estimate the effect of a person's education and work experience on the log wage earned. Now, say we want to find out how these two variables affect the decision of an East German resident to move west, i.e. we want to know $E(Y\vert{\boldsymbol{x}})$ where ${\boldsymbol{x}}$ is a $(d\times 1)$ vector containing all $d$ variables considered to be influential to the migration decision. Since $Y$ is a binary variable (i.e. a Bernoulli distributed variable), we have that

$$E(Y\vert{\boldsymbol{X}}) = P(Y=1\vert{\boldsymbol{X}}).$$ (1.8)

Thus, the regression of $Y$ on ${\boldsymbol{X}}$ can be expressed as the probability that a randomly sampled person from the East will migrate to the West, given this person's characteristics collected in the vector ${\boldsymbol{X}}$. Standard models for $P(Y=1\vert{\boldsymbol{X}})$ assume that this probability depends on ${\boldsymbol{X}}$ as follows:

$$P(Y=1\vert{\boldsymbol{X}}) = G({\boldsymbol{X}}^\top{\boldsymbol{\beta}}),$$ (1.9)

where ${\boldsymbol{X}}^\top{\boldsymbol{\beta}}$ is a linear combination of all components of ${\boldsymbol{X}}.$ It aggregates the multiple characteristics of a person into one number (therefore called the index function or simply the index), where ${\boldsymbol{\beta}}$ is an unknown vector of coefficients. $G(\bullet)$ denotes any continuous function that maps the real line to the range of $[0,1]$. $G(\bullet)$ is also called the link function, since it links the index ${\boldsymbol{X}}^\top{\boldsymbol{\beta}}$ to the conditional expectation $E(Y\vert{\boldsymbol{X}})$.

In the context of this lecture, the crucial question is precisely what parametric form these two functions take or, more generally, whether they will take any parametric form at all. For now we want to compare two models: one that assumes that $G(\bullet)$ is of a known parametric form and one that allows $G(\bullet)$ to be an unknown smooth function.

One of the most widely used fully parametric models applied to the case of binary dependent variables is the logit model. The logit model assumes that $G({\boldsymbol{X}}^\top{\boldsymbol{\beta}})$ is the (standard) logistic cumulative distribution function (cdf) for all ${\boldsymbol{X}}$. Hence, in this case

$$E(Y\vert{\boldsymbol{X}}) = P(Y=1\vert{\boldsymbol{X}}) = \frac{1}{\exp(-{\boldsymbol{X}}^\top{\boldsymbol{\beta}})}.$$ (1.10)

EXAMPLE 1.5  
In using a logit model, Burda (1993) estimated the effect of various explanatory variables on the migration decision of East German residents. The data for fitting this model were drawn from a panel study of approximately 4,000 East German households in spring 1991. We use a subsample of $n=402$ observations from the German state ``Mecklenburg-Vorpommern'' here. Due to space constraints, we merely report the estimated coefficients of three components of the index ${\boldsymbol{X}}^\top{\boldsymbol{\beta}}$, as we will refer to these estimates below:

$${\beta_0+\beta_1\cdotp\textrm{INC}+\beta_2\cdotp\textrm{AGE}}$$

$$= -2.2905 +0.0004971\cdotp\textrm{INC}-0.45499 \cdotp\textrm{AGE}$$ (1.11)

INC and AGE are used to abbreviate the household income and age of the individual. $\Box$

Figure 1.8 gives a graphical presentation of the results. Each observation is represented by a "+". As mentioned above, the characteristics of each person are transformed into an index (to be read off the horizontal axis) while the dependent variable takes on one of two values, $Y=0$ or $Y=1$ (to be read off the vertical axis). The curve plots estimates of $P(Y=1\vert{\boldsymbol{X}}),$ the probability of $Y=1$ as a function of ${\boldsymbol{X}}^\top{\boldsymbol{\beta}}$. Note that the estimates of $P(Y=1\vert{\boldsymbol{X}}),$ by assumption, are simply points on the cdf of a standard logistic distribution.

Figure 1.8: Logit fit
SPMlogit

We shall continue with Example 1.4 below, but let us pause for a moment to consider the following substantial problem: the logit model, like other parametric models, is based on rather strong functional form (linear index) and distributional assumptions, neither of which are usually justified by economic theory.

The first question to ask before developing alternatives to standard models like the logit model is: what are the consequences of estimating a logit model if one or several of these assumptions are violated? Note that this is a crucial question: if our parametric estimates are largely unaffected by model violations, then there is no need to develop and apply semiparametric models and estimators. Why would anyone put time and effort into a project that promises little return?

One can employ the tools of asymptotic statistical theory to show that violating the assumptions of the logit model leads parameter estimates to being inconsistent. That is, if the sample size goes to infinity, the logit maximum-likelihood estimator (logit-MLE) does not converge to the true parameter value in probability. While it doesn't converge to the true parameter value it does, however, converge to some other value. If this "false" value is close enough to the true parameter value then we may not care very much about this inconsistency.

Consistency is an asymptotic criterion for the performance of an estimator. That is, it looks at the properties of the estimator if the sample size grows without limits. Yet, in practice, we are dealing with finite samples. Unfortunately, the finite-sample properties of the logit maximum-likelihood estimator can not be derived analytically. Hence, we have to rely on simulations to collect evidence of its small-sample performance in the presence of misspecification. We conducted a small simulation in the context of Example 1.4 to which we now return.

Figure: Link function of the homoscedastic logit model (thin line) versus the link function of the heteroscedastic model (solid line)
SPMtruelogit

EXAMPLE 1.6  
Following Horowitz (1993) we generated data according to a heteroscedastic model with two explanatory variables, $\textrm{INC}$ and $\textrm{AGE}$. Here we considered heteroscedasticity of the form

$$\mathop{\mathit{Var}}(\varepsilon\vert{\boldsymbol{X}}=x)=\frac{1... ...{x}}^\top{\boldsymbol{\beta}})^2\right\}^2 \cdotp \mathop{\mathit{Var}}(\zeta),$$

where $\zeta$ has a (standard) logistic distribution. To give you an impression of how dramatically the true heteroscedastic model differs from the supposed homoscedastic logit model, we plotted the link functions of the two models as shown in Figure 1.9. $\Box$

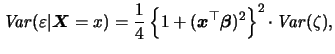
To add a sense of realism to the simulation, we set the coefficients of these variables equal to the estimates reported in (1.11). Note that the standard logit model introduced above does not allow for heteroscedasticity. Hence, if we apply the standard logit maximum-likelihood estimator to the simulated data, we are estimating under misspecification. We performed 250 replications of this estimation experiment, using the full data set with 402 observations each time. As the estimated coefficients are only identified up to scale, we compared the ratio of the true coefficients, $\beta_{INC}/\beta_{AGE}$, to the ratio of their estimated logit-MLE counterparts, $\widehat\beta_{INC}/\widehat\beta_{AGE}$. Figure 1.10 shows the sampling distribution of the logit-MLE coefficients, along with the true value (vertical line).

As we have subtracted the true value from each estimated ratio and divided this difference by the true ratio's absolute value, the true ratio is standardized to zero and differences on the horizontal axis can be interpreted as percentage deviations from the truth. In Figure 1.10, the sampling distribution of the estimated ratios is centered around $-0.11$ which is the percentage deviation from the truth of 11%. Hence, the logit-MLE underestimates the true value.

Figure: Sampling distribution of the ratio of the estimated coefficients (density estimate and mean value indicated as *) and the ratio's true value (vertical line)
SPMsimulogit

Now that we have seen how serious the consequences of model misspecification can be, we might want to learn about semiparametric estimators that have desirable properties under more general assumptions than their parametric counterparts. One way to generalize the logit model is the so-called single index model (SIM) which keeps the linear form of the index ${\boldsymbol{X}}^\top{\boldsymbol{\beta}}$ but allows the function $G(\bullet)$ in (1.9) to be an arbitrary smooth function $g(\bullet)$ (not necessarily a distribution function) that has to be estimated from the data:

$$E(Y\vert{\boldsymbol{X}})=g({\boldsymbol{X}}^\top{\boldsymbol{\beta}}),$$ (1.12)

Estimation of the single index model (1.12) proceeds in two steps:

• Firstly, the coefficient vector ${\boldsymbol{\beta}}$ has to be estimated. Methods to calculate the coefficients for discrete and continuous variables will be covered in depth later.
• Secondly, we have to estimate the unknown link function $g(\bullet)$ by nonparametrically regressing the dependent variable $Y$ on the fitted index ${\boldsymbol{X}}^\top\widehat{{\boldsymbol{\beta}}}$ where $\widehat{{\boldsymbol{\beta}}}$ is the coefficient vector we estimated in the first step. To do this, we use again a nonparametric estimator, the kernel estimator we mentioned briefly above.

Figure 1.11: Single index versus logit model
SPMsim

EXAMPLE 1.7  
Let us consider what happens if we use $\widehat{{\boldsymbol{\beta}}}$ from the logit fit and estimate the link function nonparametrically. Figure 1.11 shows this estimated link function. As before, the position of a + sign represents at the same time the values of ${\boldsymbol{X}}^\top\widehat{{\boldsymbol{\beta}}}$ and $Y$ of a particular observation, while the curve depicts the estimated link function. $\Box$

One additional remark should be made here: As you will soon learn, the shape of the estimated link function (the curve) varies with the so-called bandwidth, a parameter central in nonparametric function estimation. Thus, there is no unique estimate of the link function, and it is a crucial (and difficult) problem of nonparametric regression to find the ``best" bandwidth and thus the optimal estimate. Fortunately, there are methods to select an appropriate bandwidth. Here, we have chosen $h=0.7$ ``index units" for the bandwidth. For comparison the shapes of both the single index (solid line) and the logit (dashed line) link functions are shown ins in Figure 1.8. Even though not identical they look rather similar.

Summary

$\ast$

Parametric models are fully determined up to a parameter (vector). The fitted models can easily be interpreted and estimated accurately if the underlying assumptions are correct. If, however, they are violated then parametric estimates may be inconsistent and give a misleading picture of the regression relationship.

$\ast$

Nonparametric models avoid restrictive assumptions of the functional form of the regression function $m$. However, they may be difficult to interpret and yield inaccurate estimates if the number of regressors is large.

$\ast$

Semiparametric models combine components of parametric and nonparametric models, keeping the easy interpretability of the former and retaining some of the flexibility of the latter.