Let ![]() denote a non-negative continuous random variable describing the size
of claim (risk, loss),
denote a non-negative continuous random variable describing the size
of claim (risk, loss), ![]() and
and ![]() its distribution and probability density functions, respectively, and
its distribution and probability density functions, respectively, and ![]() the payment function
corresponding to a deductible. We consider here the simplest premium which is called the pure risk premium, see Chapter 18. The pure risk
premium
the payment function
corresponding to a deductible. We consider here the simplest premium which is called the pure risk premium, see Chapter 18. The pure risk
premium ![]() (as we consider only pure risk premium we will henceforth use the term premium meaning pure risk premium) is equal to the expectation, i.e.
(as we consider only pure risk premium we will henceforth use the term premium meaning pure risk premium) is equal to the expectation, i.e.
| (19.1) |
In the case of no deductible the payment function is obviously of the form ![]() . This means that if the loss is equal to
. This means that if the loss is equal to ![]() , the insurer pays
the whole claim amount and
, the insurer pays
the whole claim amount and
![]() .
.
We express formulae for premiums under deductibles in terms of the so-called limited expected value function (levf), namely
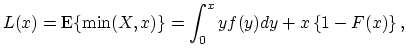 |
(19.2) |
In the following sections we illustrate premium formulae for the most important types of deductibles. All examples were created with the insurance library of XploRe.
One of the deductibles that can be incorporated in the contract is the so-called franchise deductible. In this case the insurer pays the whole claim,
if the agreed deductible amount is exceeded. More precisely, under the franchise deductible of ![]() , if the loss is less than
, if the loss is less than ![]() the insurer pays
nothing, but if the loss equals or exceeds
the insurer pays
nothing, but if the loss equals or exceeds ![]() claim is paid in full. This means that the payment function can be described as (Figure
19.1)
claim is paid in full. This means that the payment function can be described as (Figure
19.1)
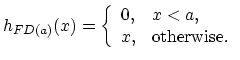 |
(19.3) |
It is worth noticing that the franchise deductible satisfies properties (i), (iii) and (iv), but not property (ii). This deductible can even work against property (ii). Since if a loss occurs, the policyholder would prefer it to be greater than or equal to the deductible.
The pure risk premium under the franchise deductible can be expressed in terms of the premium in the case of no deductible and the corresponding
limited expected value function:
| (19.4) |
An agreement between the insured and the insurer incorporating a deductible ![]() means that the insurer pays only the part of the claim which exceeds
amount
means that the insurer pays only the part of the claim which exceeds
amount ![]() . If the size of the claim falls below this amount, the claim is not covered by the contract and the insured receives no
indemnification. The payment function is thus given by
. If the size of the claim falls below this amount, the claim is not covered by the contract and the insured receives no
indemnification. The payment function is thus given by
| (19.5) |
The premium in the case of the fixed amount deductible has the following form in terms of the premium under the franchise deductible.
| (19.6) |
In the case of the proportional deductible with
![]() , each payment is reduced by
, each payment is reduced by
![]() (the insurer pays
(the insurer pays
![]() of
the claim). Consequently, the payment function is given by (Figure 19.3)
of
the claim). Consequently, the payment function is given by (Figure 19.3)
| (19.7) |
The proportional deductible satisfies properties (i), (ii), and (iv), but not property (iii), as it implies some compensation for even very small claims.
The relation between the premium under the proportional deductible and the premium in the case of no deductible has the following form.
| (19.8) |
The proportional deductible is usually combined with a minimum amount deductible so the insurer does not need to handle small claims and with a
maximum amount deductible to limit the retention of the insured. For the limited proportional deductible of ![]() with a minimum amount
with a minimum amount ![]() and
maximum amount
and
maximum amount ![]()
![]() the payment function is given by
the payment function is given by
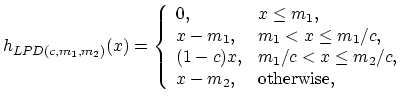 |
(19.9) |
see Figure 19.4. The limited proportional deductible satisfies all the properties.
The following formula expresses the premium under the limited proportional deductible in terms of the premium in the case of no deductible and the
corresponding limited expected value function.
| (19.10) |
There is another type of deductible that is a compromise between the franchise and fixed amount deductible. In the case of disappearing deductible
the payment depends on the loss in the following way: if the loss is less than an amount of ![]() , the insurer pays nothing; if the loss exceeds
, the insurer pays nothing; if the loss exceeds ![]() (
(![]() ) amount, the insurer pays the loss in full; if the loss is between
) amount, the insurer pays the loss in full; if the loss is between ![]() and
and ![]() , then the deductible is reduced linearly between
, then the deductible is reduced linearly between ![]() and
and ![]() . Therefore, the larger the claim, the less of the deductible
becomes the responsibility of the policyholder. The payment function is given by (Figure 19.5)
. Therefore, the larger the claim, the less of the deductible
becomes the responsibility of the policyholder. The payment function is given by (Figure 19.5)
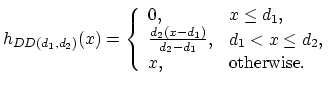 |
(19.11) |
This kind of deductible satisfies properties (i), (iii), and (iv), but similarly to the franchise deductible it works against (ii).
The following formula shows the premium under the disappearing deductible in terms of the premium in the case of no deductible and the corresponding
limited expected value function
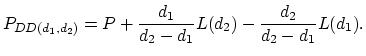 |
(19.12) |