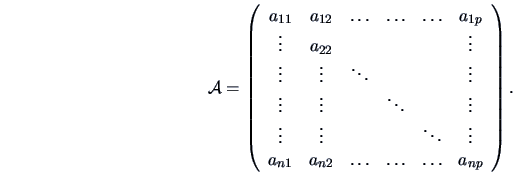
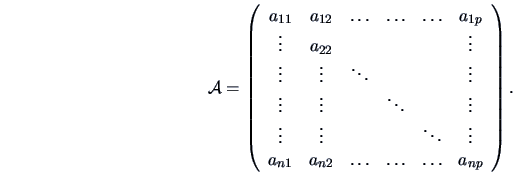
We also write ![]() for
for ![]() and
and
![]() to
indicate the numbers of rows and columns.
Vectors are matrices with one column and are denoted as
to
indicate the numbers of rows and columns.
Vectors are matrices with one column and are denoted as ![]() or
or
![]() .
Special matrices and vectors are defined in Table 2.1.
Note that we use small letters for scalars as well as for vectors.
.
Special matrices and vectors are defined in Table 2.1.
Note that we use small letters for scalars as well as for vectors.
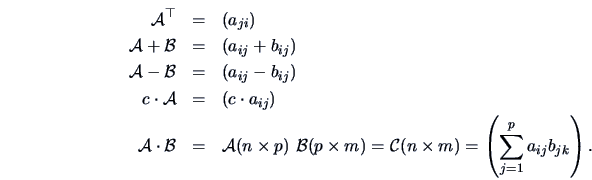
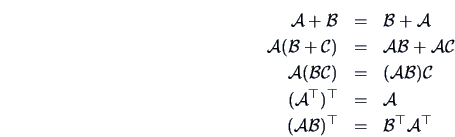

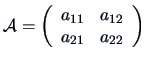 and
we can permute the digits ``1'' and ``2'' once or not at all.
So,
and
we can permute the digits ``1'' and ``2'' once or not at all.
So,

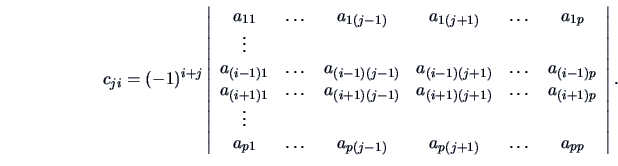
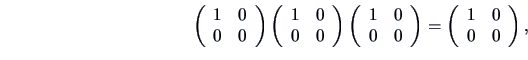
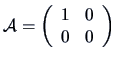 is
is
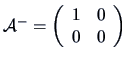 even though the inverse matrix of
even though the inverse matrix of

The determinant ![]() and the trace
and the trace
![]() can be rewritten in terms of the eigenvalues:
can be rewritten in terms of the eigenvalues:
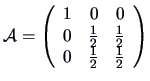 .
It is easy to verify that
.
It is easy to verify that
We know that the eigenvalues of an idempotent matrix are equal
to 0 or 1. In this case, the eigenvalues of ![]() are
are ![]() ,
, ![]() , and
, and ![]() since
since
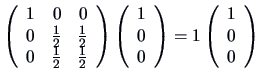 ,
,
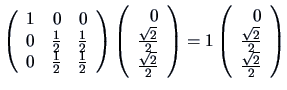 ,
and
,
and
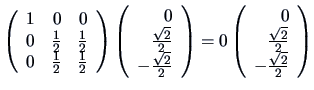 .
.
Using formulas (2.2) and (2.3),
we can calculate the trace and the determinant of ![]() from the eigenvalues:
from the eigenvalues:
![]() ,
,
![]() , and
, and
![]() .
.
![]()
| (2.4) | |||
| (2.5) | |||
| (2.6) | |||
| (2.7) |
| (2.8) | |||
| (2.9) | |||
| (2.10) | |||
| (2.11) | |||
| (2.12) | |||
| (2.13) |
| (2.16) | |||
| (2.17) |