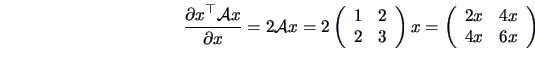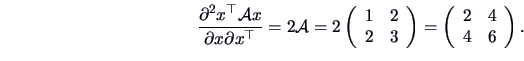2.4 Derivatives
For later sections of this book, it will be useful
to introduce matrix notation for derivatives
of a scalar function of a vector 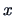 with respect to
with respect to 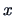 .
Consider
.
Consider
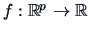 and a
and a 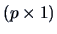 vector
vector 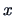 , then
, then
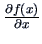 is the column vector
of partial derivatives
is the column vector
of partial derivatives
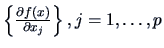 and
and
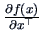 is the row vector of the same
derivative
(
is the row vector of the same
derivative
(
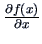 is called the gradient
of
is called the gradient
of 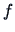 ).
).
We can also introduce second order derivatives:
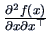 is the
is the
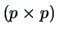 matrix of elements
matrix of elements
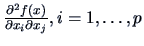 and
and
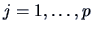 .
(
.
(
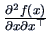 is
called the Hessian of
is
called the Hessian of 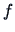 ).
).
Suppose that 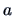 is a
is a 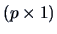 vector and that
vector and that
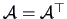 is a
is a 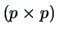 matrix. Then
matrix. Then
The Hessian of the quadratic form
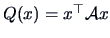 is:
is:
 |
(2.25) |
EXAMPLE 2.8
Consider the matrix
From formulas (
2.24) and (
2.25) it immediately
follows that the gradient of
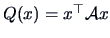
is
and the Hessian is
![]() is the
is the
![]() matrix of elements
matrix of elements
![]() and
and
![]() .
(
.
(
![]() is
called the Hessian of
is
called the Hessian of ![]() ).
).
![]() is a
is a ![]() vector and that
vector and that
![]() is a
is a ![]() matrix. Then
matrix. Then
![]() is:
is: