2.5 Partitioned Matrices
Very often we will have to consider certain groups of rows and columns of a matrix
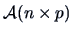 .
In the case of two groups, we have
.
In the case of two groups, we have
where
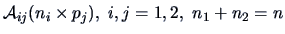 and
and 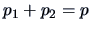 .
.
If
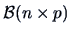 is partitioned accordingly, we have:
is partitioned accordingly, we have:
An important particular case is the square matrix
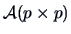 , partitioned
such that
, partitioned
such that 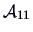 and
and 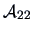 are both square matrices (i.e.,
are both square matrices (i.e.,
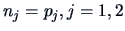 ).
It can be verified that when
).
It can be verified that when 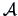 is
non-singular (
is
non-singular (
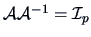 ):
):
 |
(2.26) |
where
An alternative expression can be obtained by reversing the positions of 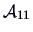 and
and 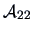 in the original matrix.
in the original matrix.
The following results will be useful if 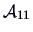 is non-singular:
is non-singular:
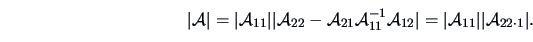 |
(2.27) |
If 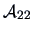 is non-singular, we have that:
is non-singular, we have that:
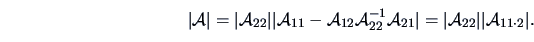 |
(2.28) |
A useful formula is derived from the alternative expressions
for the inverse and the determinant. For instance let
where 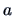 and
and 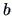 are
are 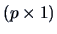 vectors and
vectors and 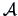 is
non-singular. We then have:
is
non-singular. We then have:
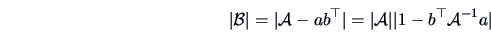 |
(2.29) |
and equating the two expressions for 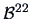 , we obtain the following:
, we obtain the following:
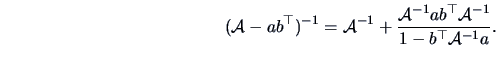 |
(2.30) |
EXAMPLE 2.9
Let's consider the matrix
We can use formula (
2.26) to calculate the inverse of a
partitioned matrix, i.e.,
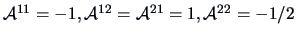
.
The inverse of
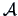
is
It is also easy to calculate the determinant of
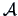
:
Let
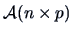 and
and
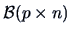 be any two
matrices and suppose that
be any two
matrices and suppose that 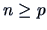 . From (2.27)
and (2.28) we can conclude that
. From (2.27)
and (2.28) we can conclude that
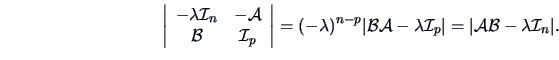 |
(2.31) |
Since both determinants on the right-hand side of (2.31)
are polynomials in 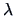 , we find that the
, we find that the 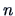 eigenvalues of
eigenvalues of
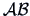 yield the
yield the 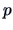 eigenvalues of
eigenvalues of
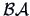 plus the eigenvalue
plus the eigenvalue 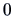 ,
, 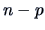 times.
times.
The relationship between the eigenvectors is described in the next theorem.
THEOREM 2.6
For
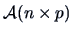
and
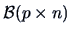
,
the non-zero eigenvalues of
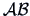
and
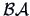
are the same and have the same multiplicity.
If
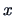
is an eigenvector of
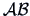
for an eigenvalue
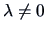
, then
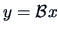
is an eigenvector of
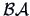
.
COROLLARY 2.2
For
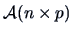
,
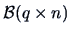
,
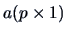
, and
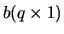
we have
The non-zero eigenvalue, if it exists, equals
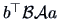
(with eigenvector
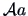
).
PROOF:
Theorem 2.6 asserts that the eigenvalues of
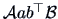 are the same as those
of
are the same as those
of
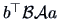 .
Note that the matrix
.
Note that the matrix
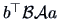 is a scalar and hence it is
its own eigenvalue
is a scalar and hence it is
its own eigenvalue 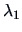 .
.
Applying
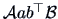 to
to 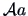 yields
yields



![]() is partitioned accordingly, we have:
is partitioned accordingly, we have:
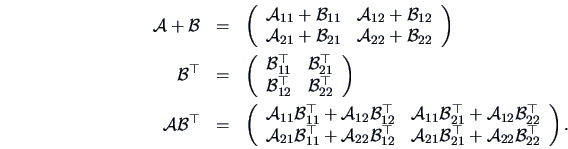
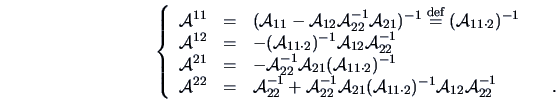
![]() is non-singular:
is non-singular:

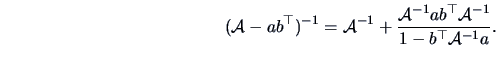


![]() and
and
![]() be any two
matrices and suppose that
be any two
matrices and suppose that ![]() . From (2.27)
and (2.28) we can conclude that
. From (2.27)
and (2.28) we can conclude that
![]() are the same as those
of
are the same as those
of
![]() .
Note that the matrix
.
Note that the matrix
![]() is a scalar and hence it is
its own eigenvalue
is a scalar and hence it is
its own eigenvalue ![]() .
.
![]() to
to ![]() yields
yields