Suppose that  has pdf
has pdf 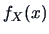 . What is the pdf of
. What is the pdf of 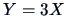 ? Or
if
? Or
if
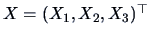 , what is the pdf of
, what is the pdf of
This is a special case of asking for the pdf of 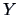 when
when
 |
(4.43) |
for a one-to-one transformation 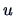 :
:
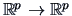 . Define the Jacobian of
. Define the Jacobian of 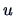 as
as
and let
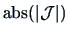 be the absolute value of the determinant
of this Jacobian. The pdf of
be the absolute value of the determinant
of this Jacobian. The pdf of 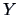 is given by
is given by
 |
(4.44) |
Using this we can answer the introductory questions, namely
with
and hence
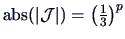 .
So the pdf of
.
So the pdf of 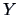 is
is
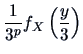 .
.
This introductory example is a special case of
The inverse transformation is
Therefore
and hence
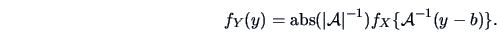 |
(4.45) |
EXAMPLE 4.12
Consider
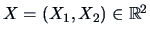
with density
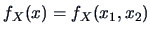
,
Then
and
Hence
EXAMPLE 4.13
Consider
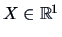
with density
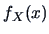
and
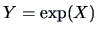
.
According to (
4.43)
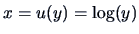
and hence the Jacobian is
The pdf of
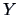
is therefore:
Summary

-
If
 has pdf
has pdf 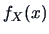 , then a transformed random vector
, then a transformed random vector 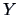 , i.e.,
, i.e.,
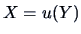 , has pdf
, has pdf
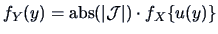 , where
, where 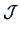 denotes the Jacobian
denotes the Jacobian
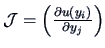 .
.

-
In the case of a linear relation
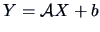 the pdf's of
the pdf's of  and
and
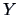 are related via
are related via
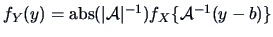 .
.
![]() has pdf
has pdf ![]() . What is the pdf of
. What is the pdf of ![]() ? Or
if
? Or
if
![]() , what is the pdf of
, what is the pdf of


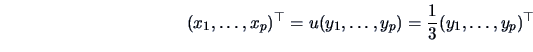

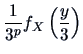 .
.

