The Wishart distribution (named after its discoverer) plays a prominent role
in the analysis of estimated covariance
matrices.
If the mean of
![]() is known to be
is known to be ![]() , then
for a data matrix
, then
for a data matrix
![]() the estimated covariance matrix is
proportional to
the estimated covariance matrix is
proportional to
![]() .
This is the point where the Wishart distribution comes in, because
.
This is the point where the Wishart distribution comes in, because
![]() has a Wishart distribution
has a Wishart distribution
![]() .
.
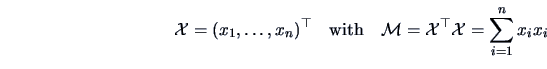
When we talk about the distribution of a matrix, we mean of course the
joint distribution of all its elements. More exactly: since
![]() is symmetric we only need to consider the elements of
the lower triangular matrix
is symmetric we only need to consider the elements of
the lower triangular matrix
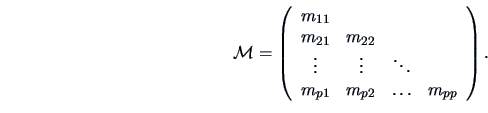 |
(5.14) |
| (5.15) |
Linear transformations of the data matrix ![]() also lead to Wishart
matrices.
also lead to Wishart
matrices.
With this theorem we can standardize Wishart matrices since
with
![]() the
distribution of
the
distribution of
![]() is
is
![]() .
Another connection to the
.
Another connection to the ![]() -distribution is given by
the following theorem.
-distribution is given by
the following theorem.
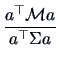 is
is
This theorem is an immediate consequence of Theorem 5.5 if we apply
the linear transformation
![]() .
Central to the analysis of covariance matrices is the next theorem.
.
Central to the analysis of covariance matrices is the next theorem.

The following properties are useful:
For further details on the Wishart distribution see Mardia et al. (1979).