12.1 Allocation Rules for Known Distributions

Discriminant analysis is a set of methods and tools used to distinguish between groups of populations $\Pi_{j}$ and to determine how to allocate new observations into groups. In one of our running examples we are interested in discriminating between counterfeit and true bank notes on the basis of measurements of these bank notes, see Table B.2. In this case we have two groups (counterfeit and genuine bank notes) and we would like to establish an algorithm (rule) that can allocate a new observation (a new bank note) into one of the groups.

Another example is the detection of ``fast'' and ``slow'' consumers of a newly introduced product. Using a consumer's characteristics like education, income, family size, amount of previous brand switching, we want to classify each consumer into the two groups just identified.

In poetry and literary studies the frequencies of spoken or written words and lengths of sentences indicate profiles of different artists and writers. It can be of interest to attribute unknown literary or artistic works to certain writers with a specific profile. Anthropological measures on ancient sculls help in discriminating between male and female bodies. Good and poor credit risk ratings constitute a discrimination problem that might be tackled using observations on income, age, number of credit cards, family size etc.

In general we have populations $\Pi_{j}, j=1,2,...,J$ and we have to allocate an observation $x$ to one of these groups. A discriminant rule is a separation of the sample space (in general $\mathbb{R}^p$) into sets $R_j$ such that if $x\in R_j$, it is identified as a member of population $\Pi _j$.

The main task of discriminant analysis is to find ``good'' regions $R_{j}$ such that the error of misclassification is small. In the following we describe such rules when the population distributions are known.

Maximum Likelihood Discriminant Rule

Denote the densities of each population $\Pi _j$ by $f_j(x)$. The maximum likelihood discriminant rule (ML rule) is given by allocating $x$ to $\Pi _j$ maximizing the likelihood $L_j(x) = f _j(x) = \max_i f_i(x)$.

If several $f_i$ give the same maximum then any of them may be selected. Mathematically, the sets $R_{j}$ given by the ML discriminant rule are defined as

$$R_{j}=\{ x : L_{j}(x) > L_{i}(x) \textrm{ for }i=1,\ldots,J, i\ne j \}.$$ (12.1)

By classifying the observation into certain group we may encounter a misclassification error. For $J=2$ groups the probability of putting $x$ into group $2$ although it is from population $1$ can be calculated as

$$p_{21}=P(X \in R_{2}\vert\Pi_{1})=\int_{R_{2}}f_{1}(x)dx.$$ (12.2)

Similarly the conditional probability of classifying an object as belonging to the first population $\Pi_{1}$ although it actually comes from $\Pi_{2}$ is

$$p_{12}=P(X \in R_{1}\vert\Pi_{2})=\int_{R_{1}}f_{2}(x)dx.$$ (12.3)

The misclassified observations create a cost $C(i\vert j)$ when a $\Pi_{j}$ observation is assigned to $R_{i}$. In the credit risk example, this might be the cost of a ``sour'' credit. The cost structure can be pinned down in a cost matrix:

		Classified population
		$\Pi_1$	$\Pi_2$
	$\Pi_1$	0	$C(2\vert 1)$
True population
	$\Pi_2$	$C(1\vert 2)$	0

Let $\pi_{j}$ be the prior probability of population $\Pi_{j}$, where ``prior'' means the a priori probability that an individual selected at random belongs to $\Pi _j$ (i.e., before looking to the value $x$). Prior probabilities should be considered if it is clear ahead of time that an observation is more likely to stem from a certain population $\Pi_{j}.$ An example is the classification of musical tunes. If it is known that during a certain period of time a majority of tunes were written by a certain composer, then there is a higher probability that a certain tune was composed by this composer. Therefore, he should receive a higher prior probability when tunes are assigned to a specific group.

The expected cost of misclassification $(ECM)$ is given by

$$ECM=C(2\vert 1)p_{21}\pi_{1}+C(1\vert 2)p_{12}\pi_{2}.$$ (12.4)

We will be interested in classification rules that keep the $ECM$ small or minimize it over a class of rules. The discriminant rule minimizing the $ECM$ (12.4) for two populations is given below.

THEOREM 12.1   For two given populations, the rule minimizing the $ECM$ is given by

$$R_{1} = \left\{ x: \frac{f_{1}(x)}{f_{2}(x)} \geq \left ( \f... ...t 1)} \right) \left( \frac{\pi_{2}}{\pi_{1}} \right) \right\}$$

$$R_{2} = \left( x: \frac{f_{1}(x)}{f_{2}(x)} < \left \{ \fra... ...t 1)} \right) \left( \frac{\pi_{2}}{\pi_{1}} \right) \right\}$$

The ML discriminant rule is thus a special case of the ECM rule for equal misclassification costs and equal prior probabilities. For simplicity the unity cost case, $C(1\vert 2)=C(2\vert 1)=1$, and equal prior probabilities, $\pi_{2}=\pi_{1}$, are assumed in the following.

Theorem 12.1 will be proven by an example from credit scoring.

EXAMPLE 12.1   Suppose that $\Pi_{1}$ represents the population of bad clients who create the cost $C(2\vert 1)$ if they are classified as good clients. Analogously, define $C(1\vert 2)$ as the cost of loosing a good client classified as a bad one. Let $\gamma$ denote the gain of the bank for the correct classification of a good client. The total gain of the bank is then

$$G(R_2) = -C(2\vert 1)\pi_{1}\int {\boldsymbol{I}}(x \in R_2) f_{1}(x)dx -C(1\vert 2)\pi_{2}\int \{1-{\boldsymbol{I}}(x \in R_2)\} f_{2}(x)dx$$

$$+\gamma \,\pi_{2}\int {\boldsymbol{I}}(x \in R_2) f_{2}(x)dx$$

$$= -C(1\vert 2)\pi_{2}+\int {\boldsymbol{I}}(x \in R_2)\{ -C(2\vert 1)\pi_{1}f_{1}(x)+(C(1\vert 2)+\gamma)\pi_{2}f_{2}(x)\}dx$$

Since the first term in this equation is constant, the maximum is obviously obtained for

$$R_2= \{\,x\,:\,-C(2\vert 1)\pi_{1}f_{1}(x)+\{C(1\vert 2)+\gamma\}\pi_{2}f_{2}(x)\,\geq 0\,\}.$$

This is equivalent to

$$R_2 = \left\{\,x\,:\,\frac{f_2(x)}{f_1(x)}\,\geq\,\frac{C(2\vert 1)\pi_{1}}{\{C(1\vert 2)+\gamma\}\pi_{2}}\right\},$$

which corresponds to the set $R_2$ in Theorem 12.1 for a gain of $\gamma=0.$

EXAMPLE 12.2   Suppose $x \in \{0,1\}$ and

$$\begin{eqnarray*} \Pi _1 &:& P(X=0)=P(X=1)=\frac{1 }{2 }\cr \Pi _2 &:& P(X=0)=\frac{1 }{4 }= 1-P(X=1). \end{eqnarray*}$$

The sample space is the set $\{0,1\}$. The ML discriminant rule is to allocate $x=0$ to $\Pi_1$ and $x=1$ to $\Pi_2$, defining the sets $R_{1}=\{0\}$, $R_{2}=\{1\}$ and $R_{1}\cup R_{2}=\{0,1\}$.

EXAMPLE 12.3   Consider two normal populations

$$\begin{eqnarray*} \Pi_1&:& N(\mu _1,\sigma ^2_1),\\ \Pi_2&:& N(\mu _2,\sigma ^2_2). \end{eqnarray*}$$

Then

$$L_i(x) = (2\pi \sigma ^2_i)^{-1/2}\exp\left \{-\frac{ 1}{2 } \left (\frac{x-\mu _i}{\sigma _i }\right )^2\right \}.$$

Hence $x$ is allocated to $\Pi_1$ ($x\in R_{1}$) if $L_{1}(x) \geq L_{2}(x)$. Note that $L_1(x)\geq L_2(x)$ is equivalent to

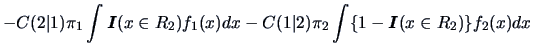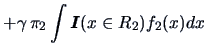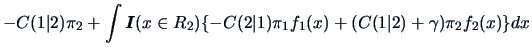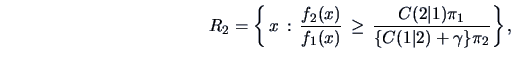
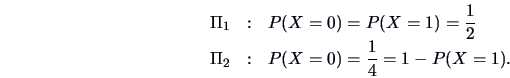
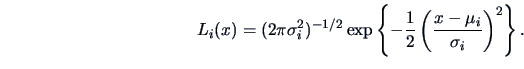
$$\frac{\sigma _2 }{\sigma _1 }\exp \left \{-\frac{1 }{2 }\left... ... (\frac{x-\mu _2}{\sigma _2 }\right )^2\right ]\right \}\geq 1$$

or

$$x^2\left (\frac{1 }{\sigma ^2_1 }-\frac{1 }{\sigma ^2_2 }\ri... ...gma ^2_2 }\right ) \leq 2 \log \frac{\sigma _2 }{\sigma _1 }.$$ (12.5)

Suppose that $\mu_1=0$, $\sigma _1=1$ and $\mu _2=1$, $\sigma _2=\frac{1 }{2 }$. Formula (12.5) leads to

$$\begin{eqnarray*} R_{1}&=&\left\{ x : x \leq \frac{1}{3} \left( 4 - \sqrt{4+6 \l... ...log(2)} \right)\right\},\\ R_{2}&=& \mathbb{R}\setminus R_{1}. \end{eqnarray*}$$

This situation is shown in Figure 12.1.

Figure 12.1: Maximum likelihood rule for normal distributions. MVAdisnorm.xpl

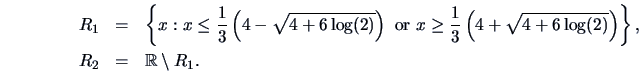
The situation simplifies in the case of equal variances $\sigma _1=\sigma _2$. The discriminant rule (12.5) is then ( for $\mu_{1}<\mu_{2}$)

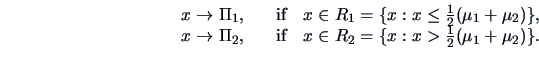$$\begin{array}{lll} x\to \Pi _1, &&\textrm{if} \quad x\in R_... ...{2}=\{ x : x > {\frac{1}{2 }}(\mu _1+\mu _2)\}. \end{array}$$ (12.6)

Theorem 12.2 shows that the ML discriminant rule for multinormal observations is intimately connected with the Mahalanobis distance. The discriminant rule is based on linear combinations and belongs to the family of Linear Discriminant Analysis (LDA) methods.

THEOREM 12.2   Suppose $\Pi_i=N_p(\mu _i,\Sigma )$.

(a)

The ML rule allocates $x$ to $\Pi _j$, where $j \in \{1,\ldots,J\}$ is the value minimizing the square Mahalanobis distance between $x$ and $\mu_{i}$:

$$\delta ^{2} (x,\mu_{i})=(x-\mu _i)^{\top}\Sigma ^{-1}(x-\mu _i)\ ,\ i=1,\ldots,J\ .$$

(b)

In the case of $J=2$,

$$x\in R_1 \iff \alpha^{\top}(x-\mu ) \geq 0 \ ,$$

where $\alpha =\Sigma^{-1}(\mu_1 - \mu_2)$ and $\mu =\frac{1 }{ 2} (\mu _1+\mu _2)$.

PROOF:
Part (a) of the Theorem follows directly from comparison of the likelihoods.

For $J=2$, part (a) says that $x$ is allocated to $\Pi_1$ if

$$(x-\mu_1)^{\top}\Sigma^{-1}(x-\mu_1)\leq (x-\mu_2)^{\top}\Sigma^{-1}(x-\mu_2)$$

Rearranging terms leads to

$$-2\mu_1^{\top} \Sigma^{-1} x +2 \mu_2^{\top} \Sigma^{-1} x +... ...^{\top} \Sigma^{-1}\mu_1-\mu_2^{\top} \Sigma^{-1}\mu_2 \leq 0,$$

which is equivalent to

$$2(\mu_2-\mu_1)^{\top} \Sigma^{-1} x + (\mu_1-\mu_2)^{\top} \Sigma^{-1}(\mu_1+\mu_2) \leq 0,$$

$$(\mu_1-\mu_2)^{\top} \Sigma^{-1} \{x-\frac{1}{2}(\mu_1+\mu_2)\}\geq 0,$$

$$\alpha^{\top}(x-\mu)\geq 0.$$

${\Box}$

Bayes Discriminant Rule

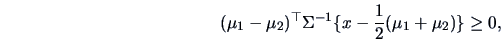
We have seen an example where prior knowledge on the probability of classification into $\Pi _j$ was assumed. Denote the prior probabilities by $\pi_{j}$ and note that $\sum_{j=1}^J \pi_{j} =1$. The Bayes rule of discrimination allocates $x$ to the $\Pi _j$ that gives the largest value of $\pi_i f_i(x)$, $\pi _jf _j(x) = \max_i \pi_i f_i(x)$. Hence, the discriminant rule is defined by $R_{j}=\{ x : \pi_{j} f_{j}(x) \geq \pi_{i} f_{i}(x) \textrm{ for }i=1,\ldots,J \}$. Obviously the Bayes rule is identical to the ML discriminant rule for $\pi _j=1/J$.

A further modification is to allocate $x$ to $\Pi _j$ with a certain probability $\phi_j(x)$, such that $\sum_{j=1}^J \phi_j(x)=1$ for all $x$. This is called a randomized discriminant rule. A randomized discriminant rule is a generalization of deterministic discriminant rules since

$$\phi_j(x) = \left\{ \begin{array}{cl} 1 &\quad \ \textrm{if... ..._if_i(x),\\ 0&\quad \ \textrm{otherwise} \end{array} \right.$$

reflects the deterministic rules.

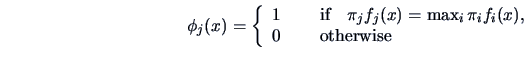
Which discriminant rules are good? We need a measure of comparison. Denote

$$p_{ij}=\int \phi _i(x)f_j(x)dx$$ (12.7)

as the probability of allocating $x$ to $\Pi _i$ if it in fact belongs to $\Pi _j$. A discriminant rule with probabilities $p_{ij}$ is as good as any other discriminant rule with probabilities $p'_{ij}$ if

$$p_{ii} \geq p'_{ii}\quad \ \textrm{for all}\quad i=1,\ldots ,J.$$ (12.8)

We call the first rule better if the strict inequality in (12.8) holds for at least one $i$. A discriminant rule is called admissible if there is no better discriminant rule.

THEOREM 12.3   All Bayes discriminant rules (including the ML rule) are admissible.

Probability of Misclassification for the ML rule ($J=2$)

Suppose that $\Pi_i=N_p(\mu _i,\Sigma )$. In the case of two groups, it is not difficult to derive the probabilities of misclassification for the ML discriminant rule. Consider for instance $p_{12}=P(x \in R_1\mid \Pi_2)$. By part (b) in Theorem 12.2 we have

$$p_{12}=P\{\alpha^{\top}(x-\mu)>0 \mid \Pi_2\}.$$

If $X \in R_2$, $\alpha^{\top}(X-\mu)\sim N\left(-\frac{1}{2}\delta^2, \delta^2\right)$ where $\delta^2=(\mu_1-\mu_2)^{\top}\Sigma^{-1}(\mu_1-\mu_2)$ is the squared Mahalanobis distance between the two populations, we obtain

$$p_{12}=\Phi\left(-\frac{1}{2}\delta\right).$$

Similarly, the probability of being classified into population 2 although $x$ stems from $\Pi_1$ is equal to $p_{21}$= $\Phi\left(-\frac{1}{2}\delta\right)$.

Classification with different covariance matrices

The minimum $ECM$ depends on the ratio of the densities $\frac{f_1(x)}{f_2(x)}$ or equivalently on the difference $\ln \{ f_1(x) \} -\ln \{ f_2(x) \}$. When the covariance for both density functions differ, the allocation rule becomes more complicated:

$$\begin{eqnarray*} R_1 & = & \left\{ x: -\frac{1}{2}x^{T} (\Sigma^{-1}_1-\Sigma^{... ...)} \right) \left( \frac{\pi_2}{\pi_1} \right) \right] \right\}, \end{eqnarray*}$$

where $k=\frac{1}{2} \ln \left( \frac{\vert\Sigma_1\vert}{\vert\Sigma_2\vert} \right) ... ...c{1}{2} (\mu^{T}_{1}\Sigma^{-1}_{1} \mu_{1}-\mu^{T}_{2}\Sigma^{-1}_{2}\mu_{2})$. The classification regions are defined by quadratic functions. Therefore they belong to the family of Quadratic Discriminant Analysis (QDA) methods. This quadratic classification rule coincides with the rules used when $\Sigma_1 =\Sigma_2$, since the term $\frac{1}{2}x^{T}(\Sigma^{-1}_{1} -\Sigma^{-1}_{2})x$ disappears.

Summary

$\ast$

Discriminant analysis is a set of methods used to distinguish among groups in data and to allocate new observations into the existing groups.

$\ast$

Given that data are from populations $\Pi_{j}$ with densities $f_{j}$, $j=1,\ldots,J$, the maximum likelihood discriminant rule (ML rule) allocates an observation $x$ to that population $\Pi_{j}$ which has the maximum likelihood $L_{j}(x)=f_{j}(x)=\max_{i} f_{i}(x)$.

$\ast$

Given prior probabilities $\pi_{j}$ for populations $\Pi_{j}$, Bayes discriminant rule allocates an observation $x$ to the population $\Pi_{j}$ that maximizes $\pi_{i} f_{i}(x)$ with respect to $i$. All Bayes discriminant rules (incl. the ML rule) are admissible.

$\ast$

For the ML rule and $J=2$ normal populations, the probabilities of misclassification are given by $p_{12}=p_{21}=\Phi\left(-\frac{1}{2}\delta\right)$ where $\delta$ is the Mahalanobis distance between the two populations.

$\ast$

Classification of two normal populations with different covariance matrices (ML rule) leads to regions defined by a quadratic function.

$\ast$

Desirable discriminant rules have a low expected cost of misclassification ($ECM$).