6.5 Itôs Lemma

A crucial tool in dealing with stochastic differential equations is Itôs lemma. If $\{ X_t, \, \, t \ge 0 \}$ is an Itô-process:

$$dX_t = \mu (X_t, t) dt + \sigma (X_t, t) \, dW_t \, ,$$ (6.8)

one is often interested in the dynamics of stochastic processes which are functions of $X_t$: $Y_t = g(X_t) \, .$ Then $\{ Y_t; \, \, t \ge 0\}$ can also be described by a solution of a stochastic differential equation from which interesting properties of $Y_t$ can be derived as for example the average growth in time $t$.

For a heuristic derivation of the equation for $\{ Y_t; \, \, t \ge 0\}$ we assume that $g$ is differentiable as many times as necessary. From a Taylor expansion it follows:

$$Y_{t+dt} - Y_t = g(X_{t+dt}) - g(X_t)$$

$$= g(X_t + dX_t) - g(X_t)$$ (6.9)

$$= \frac{dg}{dX} (X_t) \cdot dX_t + \frac{1}{2} \, \frac{d^2g}{dX^2} (X_t) \cdot (dX_t)^2 + \ldots$$

where the dots indicate the terms which can be neglected (for $dt \rightarrow 0$). Due to equation (5.8) the drift term $\mu(X_t, t)dt$ and the volatility term $\sigma (X_t, t) dW_t$ are the dominant terms since for $dt \rightarrow 0$ they are of size $dt$ and $\sqrt{dt}$ respectively.

In doing this, we use the fact that $\mathop{\text{\rm\sf E}}[(dW_t)^2] = dt$ and $dW_t = W_{t + dt} - W_t$ is of the size of its standard deviation, $\sqrt{dt}.$ We neglect terms which are of smaller size than $dt.$ Thus, we can express $(dX_t)^2$ by a simpler term:

$$(dX_t)^2 = (\mu (X_t, t) dt + \sigma (X_t, t) \, dW_t)^2$$

$$= \mu ^2 (X_t, t) (dt)^2 + 2 \mu (X_t, t)\ \sigma (X_t, t)\ dt\ dW_t + \sigma ^2 (X_t, t) (dW_t)^2 \, .$$

We see that the first and the second term are of size $(dt)^2$ and $dt \cdot \sqrt{dt}$ respectively. Therefore, both can be neglected. However, the third term is of size $dt.$ More precisely, it can be shown that $dt \rightarrow 0:$

$$(dW_t)^2 = dt .$$

Thanks to this identity, calculus rules for stochastic integrals can be derived from the rules for deterministic functions (as Taylor expansions for example). Neglecting terms which are of smaller size than $dt$ we obtain from (5.9) the following version of Itôs lemma:

Lemma 6.1 (Itôs Lemma)  

$$dY_t = dg(X_t)$$

$$= \left( \frac{dg}{dX} (X_t) \cdot \mu (X_t, t) + \frac{1}{2} \, \frac{d^2g}{dX^2} (X_t) \cdot \sigma ^2 (X_t, t) \right) dt$$

$$+ \frac{dg}{dX} (X_t) \cdot \sigma (X_t, t) \, dW_t$$

or - dropping the time index $t$ and the argument $X_t$ of the function $g$ and its derivatives:

$$dg = \left( \frac{dg}{dX} \mu (X,t) + \frac{1}{2} \, \frac{d^2g}{dX^2} \sigma ^2 (X,t)\right) dt + \frac{dg}{dX} \sigma (X,t) dW \, .$$

Example 6.1  
Consider $Y_t = \ln S_t$ the logarithm of the geometric Brownian motion. For $g(X) = \ln X$ we obtain $\frac{dg}{dX} = \frac{1}{X} \, , \frac{d^2g}{dX^2} = - \frac{1}{X^2} \, .$ Applying Itôs lemma for the geometric Brownian motion with $\mu (X,t) = \mu X\ , \, \sigma (X,t) = \sigma \, X$ we get:

$$dY_t = \big( \frac{1}{S_t} \mu \, S_t - \frac{1}{2} \, \frac{1}{S_t^2} \, \sigma ^2 \, S_t^2 \big) dt + \frac{1}{S_t} \cdot \sigma \, S_t \, dW _t$$

$$= ( \mu - \frac{1}{2} \, \sigma ^2) dt + \sigma \, dW_t$$

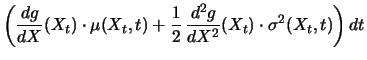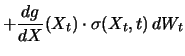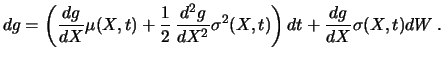
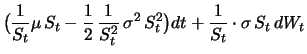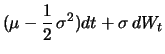The logarithm of the stock price is a generalized Wiener process with drift rate $\mu ^* = \mu - \frac{1}{2} \, \sigma ^2$ and variance rate $\sigma^2.$ Since $Y_t$ is N$(\mu ^* t, \, \sigma ^2 t)$-distributed $S_t$ is itself lognormally distributed with parameters $\mu ^*t$ and $\sigma ^2 t\, .$

A generalized version of Itôs lemma for functions $g(X,t)$ which are allowed to depend on time $t$ is:

Lemma 6.2 (Itôs lemma for functions depending explicitly on time)  

$$dg = \left( \frac{\partial g}{\partial X} \cdot \mu (X,t) + \frac... ...al g}{\partial t} \right) dt + \frac{\partial g}{\partial X} \, \sigma (X,t) dW$$ (6.10)

$Y_t = g (X_t, t)$ is again an Itô process, but this time the drift rate is augmented by an additional term $\frac{\partial g}{\partial t} (X_t, t).$