As soon as moving average coefficients are included in an
estimated model, the estimation turns out to be more difficult.
Consider the example of a simple MA(1) model
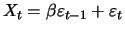 |
(12.25) |
with 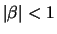 and
and
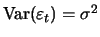 . A simple
estimator for the parameter
. A simple
estimator for the parameter 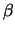 is obtained from the
Yule-Walker equations
is obtained from the
Yule-Walker equations
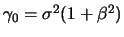 and
and
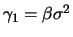 . By dividing both equations we get
. By dividing both equations we get
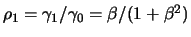 and the
solution to the quadratic equation is
and the
solution to the quadratic equation is
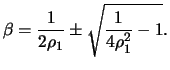 |
(12.26) |
The Yule-Walker estimator replaces in (11.26) the
theoretical autocorrelation of 1st order 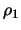 with the
estimator
with the
estimator
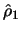 . The estimator is quite simple, but has
the disadvantage that it is asymptotically inefficient.
. The estimator is quite simple, but has
the disadvantage that it is asymptotically inefficient.
The least squares estimator leads to non-linear systems of
equations, that can only be solved with iterative numerical
algorithms. Using the example of a MA(1) process (11.25)
this is illustrated: The LS estimator is defined by
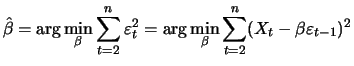 |
(12.27) |
Given that
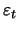 is not observed, one must turn to the
AR(
is not observed, one must turn to the
AR(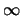 ) representation of the MA(1) process in order to find
the solution, i.e.,
) representation of the MA(1) process in order to find
the solution, i.e.,
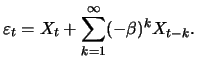 |
(12.28) |
Given
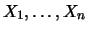 , (11.28) can be approximated by
Solving the first order conditions
we obtain a non-linear equation for
, (11.28) can be approximated by
Solving the first order conditions
we obtain a non-linear equation for 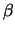 , which cannot be
explicitly solved. For the minimization problem (11.27)
one usually implements numerical optimization methods. The least
squares estimator is asymptotically efficient and has
asymptotically the same properties as the maximum likelihood (ML)
estimator.
, which cannot be
explicitly solved. For the minimization problem (11.27)
one usually implements numerical optimization methods. The least
squares estimator is asymptotically efficient and has
asymptotically the same properties as the maximum likelihood (ML)
estimator.
In the following we assume a stationary and invertible ARMA(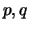 )
process with the AR(
)
process with the AR( ) representation
) representation
Maximum likelihood estimation allude to the distribution
assumptions
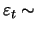
N
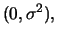
under which
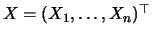 have multivariate normal
distributions with a density
with covariance matrix
have multivariate normal
distributions with a density
with covariance matrix 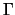 , which is given in
(11.24), and the parameter vector
The likelihood function
, which is given in
(11.24), and the parameter vector
The likelihood function 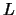 is then a density function interpreted
as a function of the parameter vector
is then a density function interpreted
as a function of the parameter vector 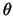 for given
observations, i.e.,
for given
observations, i.e.,
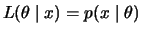 . One
chooses the respective parameter vector that maximizes the
likelihood function for the given observations, i.e., the ML
estimator is defined by
Under the assumption of the normal distribution the logarithm of
the likelihood function
. One
chooses the respective parameter vector that maximizes the
likelihood function for the given observations, i.e., the ML
estimator is defined by
Under the assumption of the normal distribution the logarithm of
the likelihood function
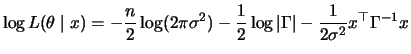 |
(12.29) |
takes on a simple form without changing the maximizer
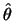 . The log-likelihood
function (11.29) is also called the exact
log-likelihood function. One notices that, in particular, the
calculation of the inverse and the determinant of the (
. The log-likelihood
function (11.29) is also called the exact
log-likelihood function. One notices that, in particular, the
calculation of the inverse and the determinant of the (
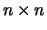 ) matrix
) matrix 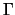 is quite involved for long time series.
Therefore one often forms an approximation to the exact
likelihood, which are good for long time series. One possibility
is use the conditional distribution
is quite involved for long time series.
Therefore one often forms an approximation to the exact
likelihood, which are good for long time series. One possibility
is use the conditional distribution
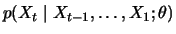 :
Under the assumption of normal distributions the conditional
distributions are normal with an expected value
and variance
The larger
:
Under the assumption of normal distributions the conditional
distributions are normal with an expected value
and variance
The larger 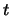 is, the better the
approximation of
by
is, the better the
approximation of
by
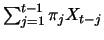 becomes. The conditional
log-likelihood function
becomes. The conditional
log-likelihood function
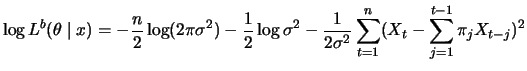 |
(12.30) |
can be calculated from the data
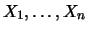 and optimized
with respect to the parameter
and optimized
with respect to the parameter 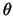 . As an initial value for
the numerical optimization algorithm the Yule-Walker estimators,
for example, can be used (except in specific cases of asymptotic
inefficiency).
. As an initial value for
the numerical optimization algorithm the Yule-Walker estimators,
for example, can be used (except in specific cases of asymptotic
inefficiency).
To compare the exact and the conditional likelihood estimators
consider a MA(1) process (11.25) with 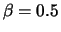 and
and
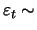 N
N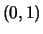 . The matrix
. The matrix 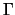 is band diagonal
with elements
is band diagonal
with elements 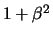 on the main diagonal and
on the main diagonal and 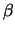 on
diagonals both above and below it. Two realizations of the process
with
on
diagonals both above and below it. Two realizations of the process
with 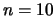 and
and 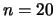 are shown in Figure 11.7.
Since the process has only one parameter, one can simply search in
the region (-1,1). This is shown for both estimators in Figure
11.8 (
are shown in Figure 11.7.
Since the process has only one parameter, one can simply search in
the region (-1,1). This is shown for both estimators in Figure
11.8 (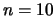 ) and 11.9 (
) and 11.9 (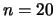 ). For the
process with
). For the
process with 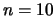 one still sees a clear discrepancy between
both likelihood functions, which for
one still sees a clear discrepancy between
both likelihood functions, which for 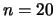 can be ignored. Both
estimators are in this case quite close to the true parameter 0.5.
can be ignored. Both
estimators are in this case quite close to the true parameter 0.5.
Fig.:
Two realizations of a MA(1) process with
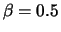 ,
,
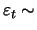 N
N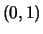 ,
, 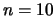 (above)
and
(above)
and 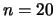 (below).
(below).
 SFEplotma1.xpl
SFEplotma1.xpl
|
|
Fig.:
Exact (solid) and conditional (dashed) likelihood functions for the MA(1) process from figure
11.7 with 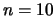 . The true parameter is
. The true parameter is
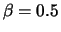 .
.
 SFElikma1.xpl
SFElikma1.xpl
|
|
Fig.:
Exact (solid) and conditional (dashed) likelihood functions for the
MA(1) process from figure
11.7 with 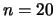 . The true parameter is
. The true parameter is
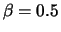 .
.
 SFElikma1.xpl
SFElikma1.xpl
|
|
Under some technical assumptions the ML estimators are consistent,
asymptotically efficient and have an asymptotic normal
distribution:
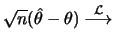
N
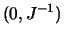
with the Fisher Information matrix
![$\displaystyle J=\mathop{\text{\rm\sf E}}\left[ -\frac{\partial^2 \log L(\theta,x)} {\partial \theta \partial \theta^\top } \right].$](sfehtmlimg2263.gif) |
(12.31) |
For the optimization of the likelihood function one frequently
uses numerical methods. The necessary condition for a maximum is
grad
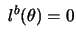
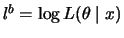 . By choosing an initial value
. By choosing an initial value
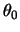 (for example, the Yule-Walker estimator), and the
Taylor approximation
one obtains the following relation:
Since generally one does not immediately hit the maximizing
parameter, one builds the iteration
with
(for example, the Yule-Walker estimator), and the
Taylor approximation
one obtains the following relation:
Since generally one does not immediately hit the maximizing
parameter, one builds the iteration
with
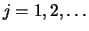 until a convergence is reached, i.e.,
until a convergence is reached, i.e.,
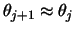 . Often it is easier to use the
expectation of the Hessian matrix, that is, the information matrix
from (11.31):
. Often it is easier to use the
expectation of the Hessian matrix, that is, the information matrix
from (11.31):
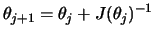 grad grad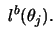 |
(12.32) |
The notation
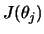 here means that (11.31) is
evaluated at
here means that (11.31) is
evaluated at 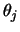 . The iteration (11.32) is called
the score-algorithm or Fisher scoring.
. The iteration (11.32) is called
the score-algorithm or Fisher scoring.
![]() is not observed, one must turn to the
AR(
is not observed, one must turn to the
AR(![]() ) representation of the MA(1) process in order to find
the solution, i.e.,
) representation of the MA(1) process in order to find
the solution, i.e.,
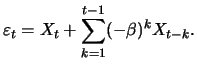
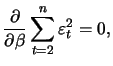
![]() )
process with the AR(
)
process with the AR(![]() ) representation
) representation
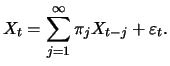
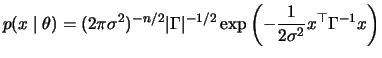
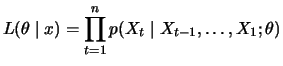
![$\displaystyle \mathop{\text{\rm\sf E}}[X_t \mid
X_{t-1},\ldots,X_1,\ldots]=\sum_{j=1}^\infty \pi_j X_{t-j}$](sfehtmlimg2251.gif)
![]() and
and
![]() N
N![]() . The matrix
. The matrix ![]() is band diagonal
with elements
is band diagonal
with elements ![]() on the main diagonal and
on the main diagonal and ![]() on
diagonals both above and below it. Two realizations of the process
with
on
diagonals both above and below it. Two realizations of the process
with ![]() and
and ![]() are shown in Figure 11.7.
Since the process has only one parameter, one can simply search in
the region (-1,1). This is shown for both estimators in Figure
11.8 (
are shown in Figure 11.7.
Since the process has only one parameter, one can simply search in
the region (-1,1). This is shown for both estimators in Figure
11.8 (![]() ) and 11.9 (
) and 11.9 (![]() ). For the
process with
). For the
process with ![]() one still sees a clear discrepancy between
both likelihood functions, which for
one still sees a clear discrepancy between
both likelihood functions, which for ![]() can be ignored. Both
estimators are in this case quite close to the true parameter 0.5.
can be ignored. Both
estimators are in this case quite close to the true parameter 0.5.
![\includegraphics[width=1\defpicwidth]{likma10.ps}](sfehtmlimg2259.gif)
![\includegraphics[width=1\defpicwidth]{likma20.ps}](sfehtmlimg2260.gif)