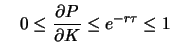In this section we consider the fundamental notion of
no-arbitrage. An arbitrage opportunity arises if it is possible to make a riskless profit.
In an ideal financial market, in which all investors dispose of
the same pieces of information and in which all investors can
react instantaneously, there should not be any arbitrage
opportunity. Since otherwise each investor would try to realize
the riskless profit instantaneously. The resulting transactions
would change the prices of the involved financial instruments such
that the arbitrage opportunity disappears.
Additionally to no-arbitrage we presume in the remaining chapter
that the financial market fulfills further simplifying assumptions
which are in this context of minor importance and solely serve to
ease the argumentation. If these assumptions hold we speak of a
perfect financial market.
ASSUMPTION (perfect financial market)
There are no arbitrage opportunities, no transaction costs,
no taxes, and no restrictions on short selling. Lending rates
equal borrowing rates and all securities are perfectly divisible.
The assumption of a perfect financial market is sufficient to
determine the value of future and forward contracts as well as some important
relations between the prices of some types of
options. Above all no mathematical model for the
price of the financial instrument is needed. However, in order to
determine the value of options more than only economic assumptions
are necessary. A detailed mathematical modelling becomes
inevitable. Each mathematical approach though has to be in line
with certain fundamental arbitrage relations being developed in
this chapter. If the model implies values of future and forward
contracts or option prices which do not fulfill these relations
the model's assumptions must be wrong.
An important conclusion drawn from the assumption of a perfect
financial market and thus from no-arbitrage will be used
frequently in the proofs to come. It is the fact that two
portfolios which have at a certain time  the same value must
have the same value at a prior time
the same value must
have the same value at a prior time 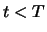 as well. Due to its
importance we will further illustrate this reasoning. We proceed
from two portfolios
as well. Due to its
importance we will further illustrate this reasoning. We proceed
from two portfolios  and
and  consisting of arbitrary financial
instruments. Their value in time
consisting of arbitrary financial
instruments. Their value in time  will be denoted by
will be denoted by 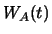 and
and 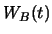 respectively. For any fixed point of time
respectively. For any fixed point of time  , we
assume that
, we
assume that
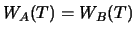 independently of the prior time
independently of the prior time  values of each financial instrument contained in
values of each financial instrument contained in  and
and 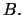 For
any prior point of time
For
any prior point of time 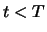 we assume without loss of generality
that
we assume without loss of generality
that
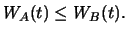 In time
In time  an investor can construct
without own financial resources a portfolio which is a combination
of
an investor can construct
without own financial resources a portfolio which is a combination
of  and
and  by buying one unit of every instrument of
by buying one unit of every instrument of 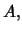 selling one unit of every instrument of
selling one unit of every instrument of  (short selling) and by
investing the difference
(short selling) and by
investing the difference
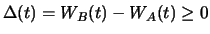 at a
fixed rate
at a
fixed rate 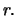 The combined portfolio has at time
The combined portfolio has at time  a value of
a value of
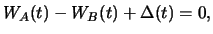
i.e. the investor has no initial costs. At time  the part of
the combined portfolio which is invested at rate
the part of
the combined portfolio which is invested at rate 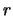 has the
compounded value
has the
compounded value
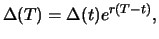 and hence the combined portfolio has a value of
and hence the combined portfolio has a value of
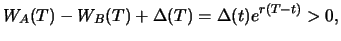
if
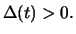 The investor made a riskless gain by investing
in the combined portfolio which contradicts the no-arbitrage
assumption. Therefore, it must hold
The investor made a riskless gain by investing
in the combined portfolio which contradicts the no-arbitrage
assumption. Therefore, it must hold
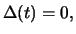 i.e.
i.e.
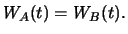
The previous reasoning can be used to determine the unknown value
of a financial derivative. For this, a portfolio  is
constructed which contains instruments with known price along with
one unit of the derivative under investigation. Portfolio
is
constructed which contains instruments with known price along with
one unit of the derivative under investigation. Portfolio  will
be compared to another portfolio
will
be compared to another portfolio  , called the duplicating
portfolio, which contains
exclusively instruments with known prices. Since the duplicating
portfolio
, called the duplicating
portfolio, which contains
exclusively instruments with known prices. Since the duplicating
portfolio  is constructed such that for certain it has the same
value at a fixed point of time
is constructed such that for certain it has the same
value at a fixed point of time  as portfolio
as portfolio  the
no-arbitrage assumption implies that both portfolios must have
the same value at any prior point of time. The value of the
financial derivative can thus be computed at any time
the
no-arbitrage assumption implies that both portfolios must have
the same value at any prior point of time. The value of the
financial derivative can thus be computed at any time  We illustrate this procedure in the following example of a forward
contract.
We illustrate this procedure in the following example of a forward
contract.
Theorem 3.1
We consider a long forward contract to buy an object which has a
price of
at time
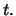
Let
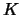
be the delivery price, and let

be the maturity date.
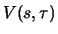
denotes the value of the
long forward contract at time

as a function of the current
price
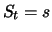
and the time to maturity
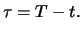
We assume
constant interest rates
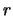
during the time to maturity.
- If the underlying object does not pay any dividends and does not
involve any costs during the time to maturity
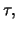 then it holds
then it holds
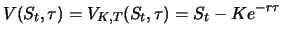 |
(3.1) |
The forward price is equal to
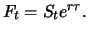
- If during the time to maturity the underlying pays at discrete time points
dividends or involves any costs whose current time
 discounted total
value is equal to
discounted total
value is equal to 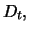 then it holds
then it holds
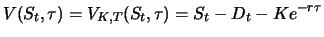 |
(3.2) |
The forward price is equal to
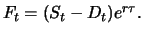
- If the underlying involves continuous costs at rate
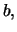 then it holds
then it holds
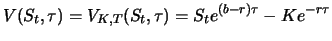 |
(3.3) |
The forward price is equal to
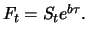
Proof:
For simplicity we assume the underlying object to be a
stock paying either discrete dividend yields whose
value discounted to time  is
is 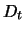 or paying a continuous
dividend yield at rate
or paying a continuous
dividend yield at rate 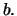 In the latter case the stock involves
continuous costs equal to
In the latter case the stock involves
continuous costs equal to 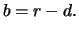 The
investor having a long position in the stock gains dividends (as
negative costs) at rate
The
investor having a long position in the stock gains dividends (as
negative costs) at rate 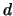 but simultaneously loses interests at
rate
but simultaneously loses interests at
rate 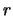 since he invested his capital in the stock instead of in
a bond with a fixed interest rate. In place of stocks, bonds,
currencies or other simple instruments can be considered as well.
since he invested his capital in the stock instead of in
a bond with a fixed interest rate. In place of stocks, bonds,
currencies or other simple instruments can be considered as well.
1. We consider at time  the following two portfolios
the following two portfolios  and
and
 :
:
- Portfolio
 :
:
- One long forward contract on a stock with delivery
price
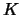 , maturing in time
, maturing in time  .
.
One long zero bond with face value 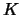 ,
maturing in time
,
maturing in time  .
.
- Portfolio
 :
:
- A long position in one unit of the stock.
At maturity  portfolio
portfolio  contains a zero bond of value
contains a zero bond of value 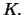 Selling this zero bond for
Selling this zero bond for 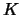 the obligation to buy the stock for
the obligation to buy the stock for
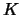 can be fulfilled. Following these transactions portfolio
can be fulfilled. Following these transactions portfolio  consists as well as portfolio
consists as well as portfolio  of one unit of the stock. Thus
both portfolios have at time
of one unit of the stock. Thus
both portfolios have at time  the same value and must
therefore, due to the no-arbitrage assumption, have the same
value at any time
the same value and must
therefore, due to the no-arbitrage assumption, have the same
value at any time  prior to
prior to 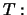
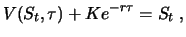 |
(3.4) |
since the value of the zero bond at time  is given by
discounting
is given by
discounting 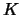 at rate
at rate
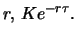 The forward price is
by definition the solution of
The forward price is
by definition the solution of
2. We consider at time  the two portfolios
the two portfolios  and
and  as given
above and add one position to portfolio
as given
above and add one position to portfolio 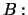
- Portfolio
 :
:
- A long position in one unit of the stock and
one short position of size
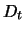 in a zero bond with interest
rate
in a zero bond with interest
rate 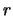 (lending an amount of money of
(lending an amount of money of 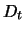 ).
).
At maturity  the dividend yields of the stock in portfolio
the dividend yields of the stock in portfolio 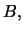 which compounded to time
which compounded to time  amount to
amount to
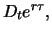 are used to
pay back the bond. Thus, both portfolios
are used to
pay back the bond. Thus, both portfolios  and
and  consist again
of one unit of the stock, and therefore they must have the same
value at any time
consist again
of one unit of the stock, and therefore they must have the same
value at any time 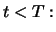
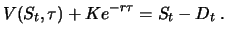 |
(3.5) |
The forward price results as in part 1 from the definition.
3. If the stock pays dividends continuously at a rate 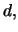 then
the reasoning is similar as in part 2. Once again, we consider at
time
then
the reasoning is similar as in part 2. Once again, we consider at
time  two portfolios
two portfolios  and
and 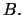 And again,
And again,  is left
unchanged,
is left
unchanged,  is now composed of the following position:
is now composed of the following position:
- Portfolio
 :
:
- A long position in
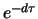 stocks.
stocks.
Reinvesting the dividends yields continuously in the stock
portfolio  consists again of exactly one stock at time
consists again of exactly one stock at time 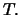 Heuristically, this can be illustrated as follows: In the time
interval
Heuristically, this can be illustrated as follows: In the time
interval
![$ [t, t+\delta]$](sfehtmlimg173.gif) the stock pays approximately, for a small
the stock pays approximately, for a small
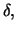 a dividend of
a dividend of
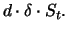 Thus, the
current total amount of stocks in the portfolio,
Thus, the
current total amount of stocks in the portfolio,
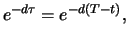 pays a total dividend yield of
pays a total dividend yield of
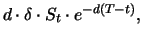 which is reinvested in the stock. Assuming
that the stock price does not change significantly in the interval
which is reinvested in the stock. Assuming
that the stock price does not change significantly in the interval
![$ [t,t+\delta],$](sfehtmlimg178.gif) i.e.
i.e.
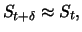 portfolio
portfolio  contains in time
contains in time 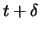 stocks. The above reasoning can be done exactly by taking the
limit
stocks. The above reasoning can be done exactly by taking the
limit
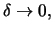 and it can be shown that portfolio
and it can be shown that portfolio
 contains at any time
contains at any time 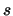 between
between  and
and  exactly
exactly
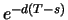 stocks. That is, for
stocks. That is, for 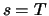 portfolio
portfolio  is composed
of exactly one stock. The same reasoning as in part 1 leads to the
conclusion that portfolio
is composed
of exactly one stock. The same reasoning as in part 1 leads to the
conclusion that portfolio  and
and  must have the same value at
any time
must have the same value at
any time  . Thus, we have
. Thus, we have
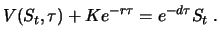 |
(3.6) |
where we have to set
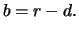 The forward price results as in
part 1 from the definition.
The forward price results as in
part 1 from the definition. 
Example 3.1
We consider a long forward contract on a 5 year bond which is
currently traded at a price of 900 EUR. The delivery price is
910 EUR, the time to maturity of the forward contract is one
year. The coupon payments of the bond of 60 EUR occur after 6 and 12 months
(the latter shortly before maturity of the forward contract). The
continuously compounded annual interest rates for 6 and 12 months are 9%
and 10% respectively. In this example we have
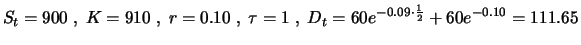 |
(3.7) |
Thus, the value of the forward contract is given by
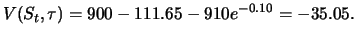 |
(3.8) |
The value of the respective short position in the forward
contract is +35.05. The price
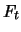
of the forward contract is
equal to
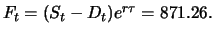
Example 3.2
Consider a long forward contract to buy 1000 Dollar. If the
investor buys the 1000 Dollar and invests this amount in a
American bond, the American interest rate can be interpreted
as a dividend yield
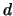
which is continuously paid. Let
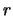
be the
home interest rate. The investment involves costs
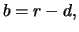
which are the difference between the American and the home
interest rate. Denoting the dollar exchange rate by
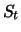
the
price of the forward contract is then given by
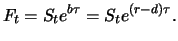 |
(3.9) |
While for
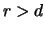
a report
results, for
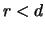
a
backwardation
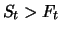
results. If
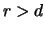
and the delivery
price is chosen to equal the current exchange rate, i.e.
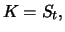
then the value of the forward contract is
Buying the forward contract at a price of
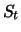
is thus more expensive
than buying the dollars immediately for the same price since in
the former case the investor can invest the money up to time

in a domestic bond paying an interest rate which is higher than the
American interest rate.
The following result states that forward and future contracts with
the same delivery price and the same time to maturity are equal,
if interest rates are constant during the contract period. We will
use the fact that by definition forward and future contracts do
not cost anything if the delivery price is chosen to be equal to
the current price of the forward contract respectively the price
of the future contract.
Theorem 3.2
If interest rates are constant during contract period, then
forward and future prices are equal.
Proof:
We proceed from the assumption that the future
contract is agreed on at time 0, and that is has a time to
maturity of 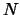 days. We assume that profits and losses are
settled (marked to market) on a daily basis at a daily interest
rate of
days. We assume that profits and losses are
settled (marked to market) on a daily basis at a daily interest
rate of 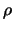 . While the forward price at the end of day 0 is
denoted by
. While the forward price at the end of day 0 is
denoted by 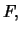 the future price at the end of day
the future price at the end of day
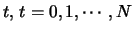 is denoted by
is denoted by 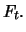 The goal is to show that
The goal is to show that
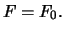 For that we construct two portfolios again:
For that we construct two portfolios again:
- Portfolio
 :
:
- A long position in
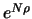 forward contracts with
delivery price
forward contracts with
delivery price  and maturity date
and maturity date 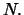
A long position in a zero bond with face value
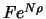 maturing in
maturing in 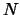 days.
days.
- Portfolio
 :
:
- A long position in futures contracts with
delivery price
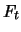 and maturity date
and maturity date 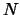 . The contracts are
bought daily such that the portfolio contains at the end of the
. The contracts are
bought daily such that the portfolio contains at the end of the
 -th day exactly
-th day exactly
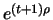 future contracts
(
future contracts
(
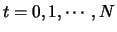 ).
).
A long position in a zero bond with face value
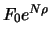 maturing in
maturing in 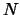 days.
days.
Purchasing a forward or a future contract does not cost anything
since their delivery prices are set to equal the current forward
or future price. Due to the marking to market procedure the holder
of portfolio  receives from day
receives from day 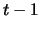 to day
to day  for each
future contract an amount of
for each
future contract an amount of
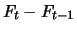 which can possibly be
negative (i.e. he has to pay).
which can possibly be
negative (i.e. he has to pay).
At maturity, i.e. at the end of day 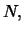 the zero bond of
portfolio
the zero bond of
portfolio  is sold at the face value
is sold at the face value
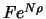 to fulfill
the terms of the forward contract and to buy
to fulfill
the terms of the forward contract and to buy 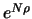 stocks at
a the delivery price
stocks at
a the delivery price 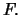 Then
Then  contains exclusively these
stocks and has a value of
contains exclusively these
stocks and has a value of
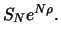 Following, we show that
portfolio
Following, we show that
portfolio  has the same value.
has the same value.
At the beginning of day  portfolio
portfolio  contains
contains 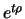 future contracts, and the holder receives due to the marking to
market procedure the amount
future contracts, and the holder receives due to the marking to
market procedure the amount
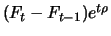 which can
possibly be negative. During the day he increases his long
position in the future contracts at zero costs such that the
portfolio contains
which can
possibly be negative. During the day he increases his long
position in the future contracts at zero costs such that the
portfolio contains
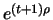 future contracts at the end of
the day. The earnings at day
future contracts at the end of
the day. The earnings at day  compounded to the maturity date
have a value of:
compounded to the maturity date
have a value of:
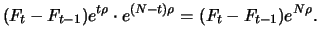 |
(3.10) |
At maturity the terms of the future contracts are fulfilled due to
the marking to market procedure. All profits and losses compounded
to day 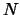 have a value of:
have a value of:
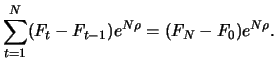 |
(3.11) |
Together with the zero bond portfolio  has at day
has at day 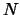 a value
of
since at maturity the future price
a value
of
since at maturity the future price 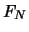 and the price
and the price 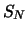 of
the underlying are obviously equal.
of
the underlying are obviously equal.
Hence, both portfolios have at day 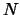 the same value and thus due
to the no-arbitrage assumption their day 0 values must be equal
as well. Since the forward contract with delivery price
the same value and thus due
to the no-arbitrage assumption their day 0 values must be equal
as well. Since the forward contract with delivery price  has a
value of 0 at day 0 due to the definition of the forward price,
the value of portfolio
has a
value of 0 at day 0 due to the definition of the forward price,
the value of portfolio  is equal to the value of the zero bond,
i.e. F (face value
is equal to the value of the zero bond,
i.e. F (face value
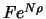 discounted to day 0).
Correspondingly, the
discounted to day 0).
Correspondingly, the 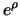 futures contained in portfolio
futures contained in portfolio  have at the end of day 0 a value of 0 due to the definition of the
future price. Again, the value of portfolio
have at the end of day 0 a value of 0 due to the definition of the
future price. Again, the value of portfolio  reduces to the
value of the zero bond. The latter has a value of
reduces to the
value of the zero bond. The latter has a value of 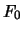 (face
value
(face
value
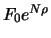 discounted to day 0). Putting things
together, we conclude that
discounted to day 0). Putting things
together, we conclude that 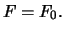

Now, we want to proof some relationship between
option prices using similar methods. The most
elementary properties are summarized in the following remark
without a proof. For that, we need the notion of the intrinsic value of an option.
Definition 3.1 (Intrinsic Value)
The
intrinsic value of a call option
at time

is given by
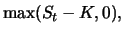
the intrinsic value of a
put option is given by
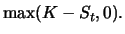
If the intrinsic value of
an option is positive we say that the option is
in the
money. If
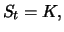
then the option is
at the money. If the intrinsic value is
negative, then the option is said to be
out of the
money.
Remark 3.1
Options satisfy the following elementary relations.
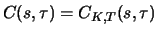
and
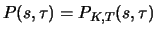
denote the time

value of a call and a put with delivery price
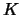
and maturity
date

, if
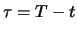
is the time to maturity and the price of
the underlying is
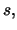
i.e.
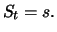
- Option prices are non negative since an exercise only takes
place if it is in the interest of the holder. An option gives
the right to exercise. The holder is not obligated to do so.
- American and European options have the same value at maturity
 since in
since in  they give the same rights to the holder. At
maturity
they give the same rights to the holder. At
maturity  the value of the option is equal to the intrinsic
value:
the value of the option is equal to the intrinsic
value:
- An American option must be traded at least at its intrinsic
value since otherwise a riskless profit can be realized by buying
and immediately exercising the option. This relation does not hold
in general for European options. The reason is that a European
option can be exercised only indirectly by means of a future
contract. The thereby involved discounting rate can possibly lead
to the option being worth less than its intrinsic value.
- The value of two American options which have different time to
maturities,
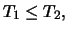 is monotonous in time to maturity:
This follows, for calls, say, using 2., 3. from the
inequality which holds at time
is monotonous in time to maturity:
This follows, for calls, say, using 2., 3. from the
inequality which holds at time 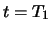 with
with
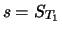
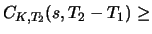 intrinsic value intrinsic value 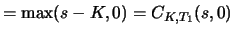 |
(3.12) |
Due to the no-arbitrage assumption the inequality must hold
for any point in time
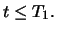 For European options this
result does not hold in general.
For European options this
result does not hold in general.
- An American option is at least as valuable as the
identically
specified European option since the American option gives more
rights to the holder.
- The value of a call is a monotonously decreasing function
of the delivery price since the right to buy is the more valuable
the lower the agreed upon delivery price. Accordingly, the value
of a put is a monotonously increasing function of the delivery price.
for
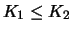 . This holds for American as well as for
European options.
. This holds for American as well as for
European options.
The value of European call and put options on the same underlying
with the same time to maturity and delivery price are closely
linked to each other without using a complicated mathematical
model.
Theorem 3.3 (Put-Call Parity
for European Options)
For the value of a European call and put option which have the
same maturity date
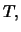
the same delivery price
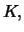
the same
underlying the following holds (where
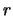
denotes the continuous
interest rate):
- If the underlying pays a dividend yield with a time
 discounted total value of
discounted total value of 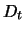 during the time to maturity
during the time to maturity 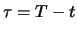 then it holds
then it holds
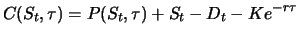 |
(3.13) |
 SFEPutCall.xpl
SFEPutCall.xpl
- If the underlying involves continuous costs of carry at rate
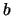 during the time to maturity
during the time to maturity 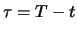 then it holds
then it holds
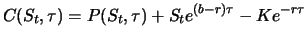 |
(3.14) |
Proof:
For simplicity, we again assume the underlying to be a stock. We
consider a portfolio  consisting of one call which will be
duplicated by a suitable portfolio
consisting of one call which will be
duplicated by a suitable portfolio  containing a put among
others.
containing a put among
others.
1. In the case of discrete dividend yields we consider at time  the following portfolio
the following portfolio 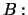
- Buy the put.
- Sell a zero bond with face value
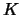 maturing
maturing 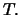
- Buy one stock.
- Sell a zero bond at the current price
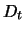 .
.
The stock in portfolio  pays dividends whose value
discounted to time
pays dividends whose value
discounted to time  is
is 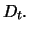 At time
At time  these dividend yields
are used to pay back the zero bond of position d). Hence this
position has a value of zero at time
these dividend yields
are used to pay back the zero bond of position d). Hence this
position has a value of zero at time 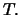 Table 2.1 shows
the value of portfolio
Table 2.1 shows
the value of portfolio  at time
at time  where we distinguished the
situations where the put is exercised (
where we distinguished the
situations where the put is exercised (
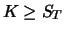 ) and where it
is not exercised.
) and where it
is not exercised.
Table 2.1:
Value of portfolio  at time
at time  (Theorem
2.3).
(Theorem
2.3).
| |
Value at timet  |
| Position |
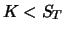 |
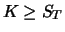 |
| a) |
0 |
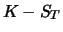 |
| b) |
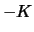 |
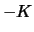 |
| c) |
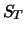 |
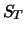 |
| d) |
0 |
0 |
| Sum |
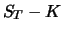 |
0 |
|
At time  portfolio
portfolio  has thus the same value
has thus the same value
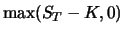 as the call. To avoid arbitrage opportunities both portfolios
as the call. To avoid arbitrage opportunities both portfolios  and
and  must have the same value at any time
must have the same value at any time  prior
prior 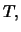 that
is it holds
that
is it holds
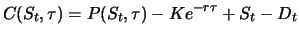 |
(3.15) |
2. In the case of continuous dividends at rate 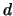 and
corresponding costs of carry
and
corresponding costs of carry 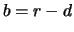 we consider the same
portfolio
we consider the same
portfolio  as in part 1. but this time without position d).
Instead we buy
as in part 1. but this time without position d).
Instead we buy
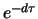 stocks in position c) whose dividends
are immediately reinvested in the same stock. If
stocks in position c) whose dividends
are immediately reinvested in the same stock. If 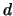 is negative,
then the costs are financed by selling stocks. Thus, portfolio
is negative,
then the costs are financed by selling stocks. Thus, portfolio  contains exactly one stock at time
contains exactly one stock at time 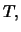 and we conclude as in
part 1. that the value of portfolio
and we conclude as in
part 1. that the value of portfolio  is at time
is at time  equal to
the value of the call.
equal to
the value of the call. 
The proof of the put-call parity holds only for European options.
For American options it may happen that the put or call are
exercised prior maturity and that both portfolios are not hold
until maturity.
The following result makes it possible to check whether prices of
options on the same underlying are consistent. If the convexity
formulated below is violated, then arbitrage opportunities arise
as we will show in the example following the proof of the next
theorem.
Theorem 3.4
The price of a (American or European) Option is a convex function
of the delivery price.
Proof:
It suffices to consider calls since the proof is analogous for
puts. The put-call parity for European options is linear in the
term which depends explicitly on 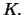 Hence, for European options
it follows immediately that puts are convex in
Hence, for European options
it follows immediately that puts are convex in 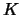 given that
calls are convex in
given that
calls are convex in 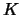 .
.
For
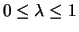 and
and 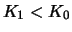 we define
we define
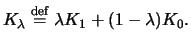 We consider a portfolio
We consider a portfolio  which
at time
which
at time 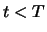 consists of one call with delivery price
consists of one call with delivery price
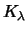 and maturity date
and maturity date 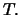 At time
At time  we duplicate this
portfolio by the following portfolio
we duplicate this
portfolio by the following portfolio 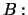
- A long position in
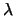 calls with delivery price
calls with delivery price 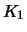 maturing in
maturing in  .
.
- A long position in
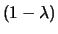 calls delivery price
calls delivery price 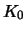 maturing in
maturing in  .
.
By liquidating both portfolios at an arbitrary point of time
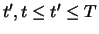 we can compute the difference in the values of
portfolio
we can compute the difference in the values of
portfolio  and
and  which is given in Table 2.2
which is given in Table 2.2
Table 2.2:
Difference in the values of portfolios  and
and  at
time
at
time 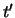 (Theorem 2.4).
(Theorem 2.4).
|
|
Value at time 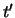 |
|
Position |
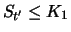 |
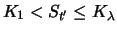 |
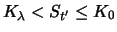 |
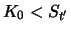 |
 1. 1. |
0 |
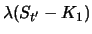 |
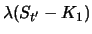 |
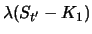 |
 2. 2. |
0 |
0 |
0 |
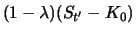 |
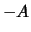 |
0 |
0 |
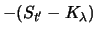 |
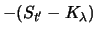 |
|
Sum |
0 |
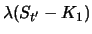 |
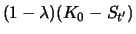 |
0 |
|
Since
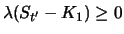 und
und
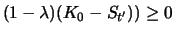 in the last row of Table 2.2 the
difference in the values of portfolio
in the last row of Table 2.2 the
difference in the values of portfolio  and
and  at time
at time 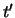 and
thus for any point of time
and
thus for any point of time 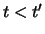 is greater than or equal to
zero. Hence, denoting
is greater than or equal to
zero. Hence, denoting
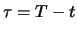 it holds
it holds
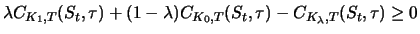 |
(3.16) |

We already said that option prices are monotonous functions of the
delivery price. The following theorem for European options is more
precise on this subject.
Theorem 3.5
For two European calls (puts) with the same maturity
date

and delivery prices
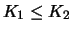
it holds at time
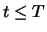
:
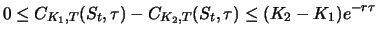 |
(3.18) |
or
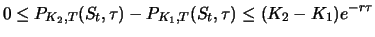 |
(3.19) |
with
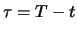
and
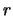
denoting the time to maturity and the
interest rate respectively. If call (put) option prices are
differentiable as a function of the delivery price, then by
taking the limit
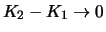
it follows
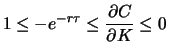 bzw. bzw.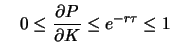 |
(3.20) |
Proof:
We proof the theorem for calls since for puts the reasoning is
analogous. For this we consider a portfolio  containing one
call with delivery price
containing one
call with delivery price 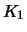 which we compare to a duplicating
portfolio
which we compare to a duplicating
portfolio 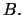 At time
At time  the latter portfolio consists of the
following two positions:
the latter portfolio consists of the
following two positions:
- A long position in one call with delivery price
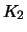 .
.
- A long position in one zero bond with face value
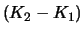 maturing in
maturing in  .
.
The difference of the value of portfolios  and
and  at time
at time  is shown in Table 2.5.
is shown in Table 2.5.
Table:
Difference in the values of portfolios  and
and  at
time
at
time  (Theorem 2.5).
(Theorem 2.5).
| |
Value at time  |
| Position |
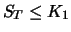 |
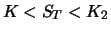 |
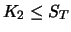 |
 1. 1. |
0 |
0 |
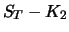 |
 2. 2. |
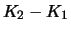 |
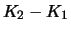 |
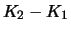 |
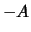 |
0 |
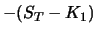 |
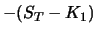 |
| Sum |
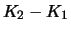 |
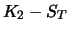 |
0 |
|
At time  portfolio
portfolio  is clearly as valuable as portfolio
is clearly as valuable as portfolio  which given the no-arbitrage assumption must hold at time
which given the no-arbitrage assumption must hold at time  as
well. We conclude:
as
well. We conclude:

![]() the same value must
have the same value at a prior time
the same value must
have the same value at a prior time ![]() as well. Due to its
importance we will further illustrate this reasoning. We proceed
from two portfolios
as well. Due to its
importance we will further illustrate this reasoning. We proceed
from two portfolios ![]() and
and ![]() consisting of arbitrary financial
instruments. Their value in time
consisting of arbitrary financial
instruments. Their value in time ![]() will be denoted by
will be denoted by ![]() and
and ![]() respectively. For any fixed point of time
respectively. For any fixed point of time ![]() , we
assume that
, we
assume that
![]() independently of the prior time
independently of the prior time ![]() values of each financial instrument contained in
values of each financial instrument contained in ![]() and
and ![]() For
any prior point of time
For
any prior point of time ![]() we assume without loss of generality
that
we assume without loss of generality
that
![]() In time
In time ![]() an investor can construct
without own financial resources a portfolio which is a combination
of
an investor can construct
without own financial resources a portfolio which is a combination
of ![]() and
and ![]() by buying one unit of every instrument of
by buying one unit of every instrument of ![]() selling one unit of every instrument of
selling one unit of every instrument of ![]() (short selling) and by
investing the difference
(short selling) and by
investing the difference
![]() at a
fixed rate
at a
fixed rate ![]() The combined portfolio has at time
The combined portfolio has at time ![]() a value of
a value of
![]() is
constructed which contains instruments with known price along with
one unit of the derivative under investigation. Portfolio
is
constructed which contains instruments with known price along with
one unit of the derivative under investigation. Portfolio ![]() will
be compared to another portfolio
will
be compared to another portfolio ![]() , called the duplicating
portfolio, which contains
exclusively instruments with known prices. Since the duplicating
portfolio
, called the duplicating
portfolio, which contains
exclusively instruments with known prices. Since the duplicating
portfolio ![]() is constructed such that for certain it has the same
value at a fixed point of time
is constructed such that for certain it has the same
value at a fixed point of time ![]() as portfolio
as portfolio ![]() the
no-arbitrage assumption implies that both portfolios must have
the same value at any prior point of time. The value of the
financial derivative can thus be computed at any time
the
no-arbitrage assumption implies that both portfolios must have
the same value at any prior point of time. The value of the
financial derivative can thus be computed at any time ![]() We illustrate this procedure in the following example of a forward
contract.
We illustrate this procedure in the following example of a forward
contract.
![]() the following two portfolios
the following two portfolios ![]() and
and
![]() :
:
![]() the two portfolios
the two portfolios ![]() and
and ![]() as given
above and add one position to portfolio
as given
above and add one position to portfolio ![]()
![]() then
the reasoning is similar as in part 2. Once again, we consider at
time
then
the reasoning is similar as in part 2. Once again, we consider at
time ![]() two portfolios
two portfolios ![]() and
and ![]() And again,
And again, ![]() is left
unchanged,
is left
unchanged, ![]() is now composed of the following position:
is now composed of the following position:
![]() the zero bond of
portfolio
the zero bond of
portfolio ![]() is sold at the face value
is sold at the face value
![]() to fulfill
the terms of the forward contract and to buy
to fulfill
the terms of the forward contract and to buy ![]() stocks at
a the delivery price
stocks at
a the delivery price ![]() Then
Then ![]() contains exclusively these
stocks and has a value of
contains exclusively these
stocks and has a value of
![]() Following, we show that
portfolio
Following, we show that
portfolio ![]() has the same value.
has the same value.
![]() portfolio
portfolio ![]() contains
contains ![]() future contracts, and the holder receives due to the marking to
market procedure the amount
future contracts, and the holder receives due to the marking to
market procedure the amount
![]() which can
possibly be negative. During the day he increases his long
position in the future contracts at zero costs such that the
portfolio contains
which can
possibly be negative. During the day he increases his long
position in the future contracts at zero costs such that the
portfolio contains
![]() future contracts at the end of
the day. The earnings at day
future contracts at the end of
the day. The earnings at day ![]() compounded to the maturity date
have a value of:
compounded to the maturity date
have a value of:
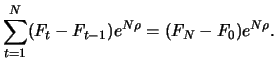
![]() the same value and thus due
to the no-arbitrage assumption their day 0 values must be equal
as well. Since the forward contract with delivery price
the same value and thus due
to the no-arbitrage assumption their day 0 values must be equal
as well. Since the forward contract with delivery price ![]() has a
value of 0 at day 0 due to the definition of the forward price,
the value of portfolio
has a
value of 0 at day 0 due to the definition of the forward price,
the value of portfolio ![]() is equal to the value of the zero bond,
i.e. F (face value
is equal to the value of the zero bond,
i.e. F (face value
![]() discounted to day 0).
Correspondingly, the
discounted to day 0).
Correspondingly, the ![]() futures contained in portfolio
futures contained in portfolio ![]() have at the end of day 0 a value of 0 due to the definition of the
future price. Again, the value of portfolio
have at the end of day 0 a value of 0 due to the definition of the
future price. Again, the value of portfolio ![]() reduces to the
value of the zero bond. The latter has a value of
reduces to the
value of the zero bond. The latter has a value of ![]() (face
value
(face
value
![]() discounted to day 0). Putting things
together, we conclude that
discounted to day 0). Putting things
together, we conclude that ![]()
![]()
![]() the following portfolio
the following portfolio ![]()
![]() and
corresponding costs of carry
and
corresponding costs of carry ![]() we consider the same
portfolio
we consider the same
portfolio ![]() as in part 1. but this time without position d).
Instead we buy
as in part 1. but this time without position d).
Instead we buy
![]() stocks in position c) whose dividends
are immediately reinvested in the same stock. If
stocks in position c) whose dividends
are immediately reinvested in the same stock. If ![]() is negative,
then the costs are financed by selling stocks. Thus, portfolio
is negative,
then the costs are financed by selling stocks. Thus, portfolio ![]() contains exactly one stock at time
contains exactly one stock at time ![]() and we conclude as in
part 1. that the value of portfolio
and we conclude as in
part 1. that the value of portfolio ![]() is at time
is at time ![]() equal to
the value of the call.
equal to
the value of the call. ![]()
![]() and
and ![]() we define
we define
![]() We consider a portfolio
We consider a portfolio ![]() which
at time
which
at time ![]() consists of one call with delivery price
consists of one call with delivery price
![]() and maturity date
and maturity date ![]() At time
At time ![]() we duplicate this
portfolio by the following portfolio
we duplicate this
portfolio by the following portfolio ![]()
![]() und
und
![]() in the last row of Table 2.2 the
difference in the values of portfolio
in the last row of Table 2.2 the
difference in the values of portfolio ![]() and
and ![]() at time
at time ![]() and
thus for any point of time
and
thus for any point of time ![]() is greater than or equal to
zero. Hence, denoting
is greater than or equal to
zero. Hence, denoting
![]() it holds
it holds
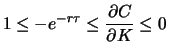 bzw.
bzw.