18.2 Individual Risk Model

We consider here a certain portfolio of insurance policies and the total amount of claims arising from it during a given period (usually a year). Our aim is to determine the joint premium for the whole portfolio that will cover the accumulated risk connected with all policies.

In the individual risk model, which is widely used in applications, especially in life and health insurance, we assume that the portfolio consists of $n$ insurance policies and the claim made in respect of the policy $k$ is denoted by $X_k$. Then the total, or aggregate, amount of claims is

$$S=X_1+X_2+\ldots+X_n,$$ (18.7)

where $X_k$ is the loss on insured unit $k$ and $n$ is the number of risk units insured (known and fixed at the beginning of the period). The $X_k$'s are usually postulated to be independent random variables (but not necessarily identically distributed), so we will make such assumption in this section. Moreover, the individual risk model discussed here will not recognize the time value of money because we will consider only models for short periods.

The claim amount variable $X_k$ for each policy is usually presented as

$$X_k=I_kB_k,$$ (18.8)

where random variables $I_1,\ldots,I_n,B_1,\ldots,B_n$ are independent. The random variable $I_k$ indicates whether or not the $k$th policy produced a payment. If the claim has occurred, then $I_k=1$; if there has not been any claim, $I_k=0$. We denote $q_k = \textrm{P}(I_k=1)$ and $1-q_k=\textrm{P}(I_k=0)$. The random variable $B_k$ can have an arbitrary distribution and represents the amount of the payment in respect of the $k$th policy given that the payment was made.

In Section 18.2.1 we present general formulae for the premiums introduced in Section 18.1. In Section 18.2.2 we apply the normal approximation to obtain closed-form formulae for both the exponential and quantile premiums. Finally in Section 18.2.3, we illustrate the behavior of these premiums on a real-life data describing losses resulting from catastrophic events in the USA.

18.2.1 General Premium Formulae

In order to find formulae for the ``pragmatic'' premiums, let us assume that the expectations and variances of $B_k$'s exist and denote $\mu_k=\mathop{\textrm{E}}(B_k)$ and $\sigma_k^2=\mathop{\textrm{Var}}(B_k)$, $k=1,2,\ldots,n$. Then

$$\mathop{\textrm{E}}(X_k)=\mu_k q_k,$$ (18.9)

and the mean of the total loss in the individual risk model is given by

$$\mathop{\textrm{E}}(S)=\sum_{k=1}^{n}\mu_k q_k.$$ (18.10)

The variance of $X_k$ can be calculated as follows:

$$\mathop{\textrm{Var}}(X_k) = \mathop{\textrm{Var}}\{\mathop{\textrm{E}}(X_k\vert I_k)\} + \mathop{\textrm{E}}\{\mathop{\textrm{Var}}(X_k\vert I_k)\}$$ (18.11)

$$= \mathop{\textrm{Var}}\{I_k \mathop{\textrm{E}}(B_k)\} + \mathop{\textrm{E}}\{I_k \mathop{\textrm{Var}}(B_k)\}$$

$$= \{\mathop{\textrm{E}}(B_k)\}^2 \mathop{\textrm{Var}}(I_k) + \mathop{\textrm{Var}}(B_k) \mathop{\textrm{E}}(I_k)$$

$$= \mu_k^2q_k(1-q_k)+\sigma_k^2 q_k.$$

Applying the assumption of independent $X_k$'s, the variance of $S$ is of the form:

$$\mathop{\textrm{Var}}(S)=\sum_{k=1}^{n} \left\{\mu_k^2q_k(1-q_k)+\sigma_k^2 q_k\right\}.$$ (18.12)

Now we can easily obtain the following formulae for the individual risk model:

• pure risk premium
  

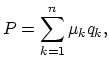  $$P=\sum_{k=1}^{n}\mu_k q_k,$$ (18.13)

  
  

• premium with safety loading
  

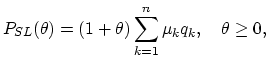  $$P_{SL}(\theta)=(1+\theta)\sum_{k=1}^{n}\mu_k q_k, \quad \theta\geq 0,$$ (18.14)

  
  

• premium with variance loading
  

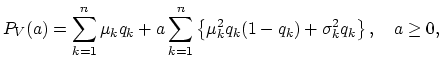  $$P_{V}(a)=\sum_{k=1}^{n}\mu_k q_k+a\sum_{k=1}^{n}\left\{\mu_k^2q_k(1-q_k)+\sigma_k^2 q_k\right\}, \quad a\geq 0,$$ (18.15)

  
  

• premium with standard deviation loading
  

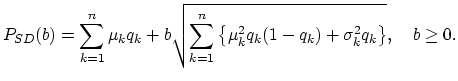  $$P_{SD}(b)=\sum_{k=1}^{n}\mu_k q_k+b\sqrt{\sum_{k=1}^{n}\left\{\mu_k^2q_k(1-q_k)+\sigma_k^2 q_k\right\}}, \quad b\geq 0.$$ (18.16)

  
  

If we assume that for each $k=1,2,\ldots,n$ the moment generating function $M_{B_k}(t)$ exists, then

$$M_{X_k}(t)=1-q_k+q_k M_{B_k}(t),$$ (18.17)

and hence

$$M_S(t)=\prod_{k=1}^{n}\left\{1-q_k+q_k M_{B_k}(t)\right\}.$$ (18.18)

This leads to the following formula for the exponential premium:

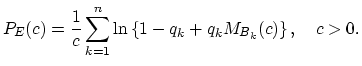$$P_{E}(c)=\frac{1}{c}\sum_{k=1}^{n}\ln \left\{1-q_k+q_k M_{B_k}(c)\right\}, \quad c>0.$$ (18.19)

In the individual risk model, claims of an insurance company are modeled as a sum of the claims of many insured individuals. Therefore, in order to find the quantile premium given by

$$P_{Q}(\varepsilon)=F^{-1}_{S}(1-\varepsilon), \quad \varepsilon\in(0,1),$$ (18.20)

the distribution of the sum of independent random variables has to be determined. There are methods to solve this problem, see Bowers et al. (1997) and Panjer and Willmot (1992). For example, one can use the convolution of the probability distributions of $X_1,X_2,\ldots,X_n$. However in practice it can be a very complex task that involves numerous calculations. In many cases the result cannot be represented by a simple formula. Therefore, approximations for the distribution of the sum are often used.

18.2.2 Premiums in the Case of the Normal Approximation

The distribution of the total claim in the individual risk model can be approximated by means of the central limit theorem (Bowers et al.; 1997). In such case it is sufficient to evaluate means and variances of the individual loss random variables, sum them to obtain the mean and variance of the aggregate loss of the insurer and apply the normal approximation. However, it is important to remember that the quality of this approximation depends not only on the size of the portfolio, but also on its homogeneity.

The approximation of the distribution of the total loss $S$ in the individual risk model can be applied to find a simple expression for the quantile premium. If the distribution of $S$ is approximated by a normal distribution with mean $\mathop{\textrm{E}}(S)$ and variance $\mathop{\textrm{Var}} (S)$, the quantile premium can be written as

$$P_{Q}(\varepsilon)=\sum_{k=1}^{n}\mu_k q_k+\Phi^{-1}(1-\varepsilon)\sqrt{\sum_{k=1}^{n}\left\{\mu_k^2q_k(1-q_k)+\sigma_k^2 q_k\right\}},$$ (18.21)

where $\varepsilon\in(0,1)$ and $\Phi(\cdot)$ denotes the standard normal distribution function. It is the same premium as the premium with standard deviation loading with $b=\Phi^{-1}(1-\varepsilon)$.

Moreover, in the case of this approximation, it is possible to express the exponential premium as

$$P_{E}(c)=\sum_{k=1}^{n}\mu_k q_k+\frac{c}{2}\sum_{k=1}^{n}\left\{\mu_k^2q_k(1-q_k)+\sigma_k^2 q_k\right\}, \quad c>0,$$ (18.22)

and it is easy to notice, that this premium is equal to the premium with variance loading with $a=c/2$.

Since the distribution of $S$ is approximated by the normal distribution with the same mean value and variance, premiums defined in terms of the expected value of the aggregate claims are given by the same formulae as in Section 18.2.1.

18.2.3 Examples

18.2.3.0.1 Quantile premium for the individual risk model with $B_k$'s log-normally distributed.

The insurance company holds $n=500$ policies $X_k$. The claims arising from policies can be represented as independent identically distributed random variables. The actuary estimates that each policy generates a claim with probability $q_k=0.05$ and the claim size, given that the claim happens, is log-normally distributed. The parameters of the log-normal distribution correspond to the real-life data describing losses resulting from catastrophic events in the USA, i.e. $\mu_k=18.3806$ and $\sigma_k=1.1052$ (see Chapter 13).

As the company wants to assure that the probability of losing any money is less than a specific value $\varepsilon$, the actuary is asked to calculate the quantile premium. The actuary wants to compare the quantile premium given by the general formula (18.20) with the one (18.21) obtained from the approximation of the aggregate claims.

The distribution of the total claim in this model can be approximated by the normal distribution with mean $4.4236 \cdot 10^9$ and variance $2.6160 \cdot 10^{18}$.

Figure 18.1 shows the quantile premium in the individual risk model framework for $\varepsilon \in (0.01, 0.1)$. The exact premium is drawn with the solid blue line whereas the premium calculated on the base of the normal approximation is marked with the dashed red line. Because of the complexity of analytical formulae, the exact quantile premium for the total claim amount was obtained using numerical simulations. The simulation-based approach is the reason for the line being jagged. A better smoothness can be achieved by performing a larger number of Monte Carlo simulations (here we performed 10000 simulations).

We can observe now that the approximation seems to fit well for larger $\varepsilon$ and worse for small $\varepsilon$. This is specific for the quantile premium. The effect is caused by the fact that even if two distribution functions $F_1(x), F_2(x)$ are very close to each other, their inverse functions $F_1^{-1}(y), F_2^{-1}(y)$ may differ significantly for $y$ close to 1.

Figure 18.1: Quantile premium for the individual risk model with $B_k$'s log-normally distributed. The exact premium (solid blue line) and the premium resulting for the normal approximation of the aggregate claims (dashed red line).

STFprem01.xpl

18.2.3.0.2 Exponential premium for the individual risk model with $B_k$'s gamma distributed.

Because the company has a specific risk strategy described by the exponential utility function, the actuary is asked to determine the premium for the same portfolio of $500$ independent policies once again but now with respect to the risk aversion parameter $c$. The actuary is also asked to use a method of calculation that provides direct results and does not require Monte Carlo simulations.

This time the actuary has decided to describe the claim size, given that the claim happens, by the gamma distribution with $\alpha =0.9185$ and $\beta=5.6870\cdot 10^{-9}$, see Chapter 13. The choice of the gamma distribution guarantees a simple analytical form of the premium, namely

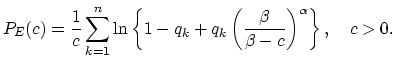$$P_{E}(c)=\frac{1}{c}\sum_{k=1}^{n}\ln \left\{1-q_k+q_k \left(\frac{\beta}{\beta-c}\right)^{\alpha}\right\}, \quad c>0.$$ (18.23)

On the other hand, the actuary can use formula (18.22) applying the normal approximation of the aggregate claims with mean $4.0377 \cdot 10^9$ and variance $1.3295 \cdot 10^{18}$.

Figure 18.2 shows the exponential premiums resulting from both approaches with respect to the risk aversion parameter $c$. A simple pattern can be observed - the more risk averse the customer is, the more he or she is willing to pay for the risk protection. Moreover, the normal approximation gives better results for smaller values of $c$.

Figure: Exponential premium for the individual risk model with $B_k$'s generated from the gamma distribution. The exact premium (solid blue line) and the premium resulting for the normal approximation of the aggregate claims (dashed red line).

STFprem02.xpl